Статистики, их выборочные распределения и точечные оценки параметров распределений в EXCEL

В статье напомним некоторые понятия математической статистики: выборка, статистика, точечная оценка, выборочное распределение. Продемонстрируем в MS EXCEL сходимость некоторых распределений статистик к нормальному распределению, распределению ХИ-квадрат, распределению Стьюдента и F - распределению.

В математической статистике обычно выделяют 2 основных направления исследований. Первое направление связано с оценкой неизвестных параметров распределения; второе – с проверкой статистических гипотез . В этой статье рассмотрим подходы, используемые для оценки неизвестных параметров распределения.

Сначала напомним основные понятия математической статистики, необходимые для оценки параметров.

О выборке

В математической статистике вероятностная модель явления (распределение) определена с точностью до неизвестных параметров. Например, предполагается известным, что случайная величина распределена по нормальному закону , но неизвестны его параметры ( среднее и дисперсия ). Отсутствие сведений о параметрах компенсируется тем, что нам позволено проводить «пробные» испытания ( выборки , samples) и на их основе восстанавливать недостающую информацию.

Почему необходимо иметь результат более чем одного испытания? Потому, что результаты одного испытания менее точны, чем среднее значение выборки .

Число испытаний в выборке обозначим n. Каждое испытание состоит в том, что мы случайным образом выбираем один объект генеральной совокупности ( population ) и записываем его характеристику X. Полученный таким образом ряд чисел Х ₁ ,..., Х _n будем называть случайной выборкой объема n, а числа X _i - элементами выборки . Элементы выборки являются независимыми случайными величинами и, как все случайные величины, имеет функцию распределения (одинаковую для всех Х _i ).

После того, как выборка была получена, следующим вопросом является то, каким образом получить информацию о неизвестном распределении:

• во-первых, из выборки можно оценить среднее и дисперсию исходного распределения (будем называть их показателями распределения).
• во-вторых, можно оценить параметр(ы) распределения (см. ниже).

Примечание : Для некоторых распределений дисперсия и стандартное отклонение случайной величинымогут быть одновременно показателями и параметрами распределения (например, для нормального распределения ).

О статистиках и точечной оценке параметров распределения

На основании значений выборки можно вычислить различные величины, например, сумму, среднее арифметическое или сумму квадратов значений выборки . Эти или иные другие величины, полученные на основании значений выборки , называются статистиками ( statistics ) .

На основе выборки можно построить, вообще говоря, бесконечное число статистик , но лишь некоторые статистики могут служить оценкой параметров исходного распределения, из которого была взята выборка . Например, среднее значение выборки из нормального распределения служит оценкой параметра μ этого распределения; а стандартное отклонение выборки служит оценкой его параметра σ .

Примечание : Для нормального распределения μ является как параметром распределения, так и его средним значением ( математическим ожиданием ), а также медианой и модой .

Процедура оценки параметров распределения с помощью статистик называется точечной оценкой ( point estimation ), а сама статистика называется точечной оценкой неизвестного параметра ( point estimator ) .

Примечание : Про оценку параметров конкретного распределения можно прочитать в статье, относящейся к этому распределению (см. заглавную статью о распределениях ).

Выборочные распределения статистик

Т.к. статистики получены из случайной выборки , то они сами являются случайными величинами и, соответственно, имеют свое собственное распределение (в общем случае не обязательно совпадающее с исходным распределением, из которого взята выборка ). Это распределение называется выборочным распределением (sampling distribution).

Чтобы определить точность оценки необходимо исследовать ее выборочное распределение , особенно среднее и дисперсию этого распределения . Т.к. на основе выборки можно построить множество различных статистик , то необходимо сформулировать критерии, которые позволят выбрать «лучшие» статистики для оценки параметров распределения. Например, если среднее значение выборочного распределения статистики совпадает с оцениваемым параметром (для всевозможных значений параметра), то такая статистика называется несмещенной оценкой . Также очевидно, что среди двух несмещенных оценок лучше та, чья дисперсия соответствующего выборочного распределения меньше . Такая статистика называется несмещённой оценкой с минимальной дисперсией (MVUE, minimum variance unbiased estimator).

Во многих случаях выборочное распределение статистики , такой как, например, среднее выборки , близко к нормальному даже тогда, когда распределение отдельных элементов выборки отличается от нормального . Этот результат, который называют Центральной предельной теоремой , упрощает статистический вывод , поскольку известно, как вычислять вероятность для нормального распределения , что в свою очередь позволяет получить информацию о генеральной совокупности (об исходном распределении, из которого была взята выборка ).

Некоторые статистики и их распределения играют важную роль в математической статистике. Например, они позволяют вычислить точечную оценку параметра и построить соответствующий доверительный интервал , а также провести процедуру проверки гипотез .

Ниже рассмотрим некоторые важные статистики , вычисленные на основе выборки из нормального распределения.

Выборочное распределение среднего

Пусть выборка извлекается из нормального распределения с параметрами N(μ;σ ² ). Рассмотрим статистику Х _ср ( среднее выборки ):

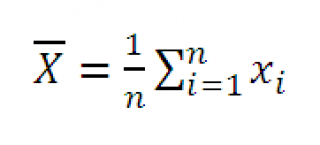
Из Центральной предельной теоремы известно, что выборочное распределение статистики Х _ср ( выборочное распределение среднего ) при достаточно большом размере выборки n стремится к нормальному распределению с параметрами N(μ;σ ² /n).

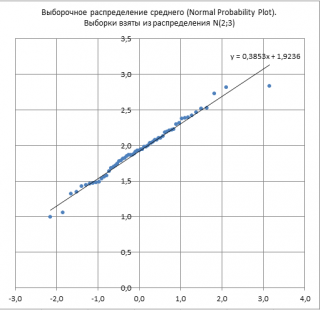
Проверим это утверждение в MS EXCEL (см. файл примера Лист Нормальное ). Для этого возьмем 60 значений выборочных средних (Хср), вычисленныхна основе 60 случайных выборок, взятых из нормального распределения с параметрами N(μ;σ ² ). Размер выборки n взят равным 50.

С помощью Графика проверки на нормальность (Normal Probability Plot) покажем, что выборочное распределение среднего соответствует нормальному закону .

Как видно из рисунка выше, средние значения выборок хорошо укладываются на прямой, что позволяет сделать вывод о нормальности распределения. Параметры этого распределения можно, например, с помощью линии регрессии, которые близки к расчетным.

Использование выборочного распределения статистики Х _ср позволяет при ИЗВЕСТНОЙ дисперсии исходного нормального распределения построить доверительный интервал для оценки математического ожидания этого распределения , а также провести проверку гипотез .

Выборочное распределение статистики

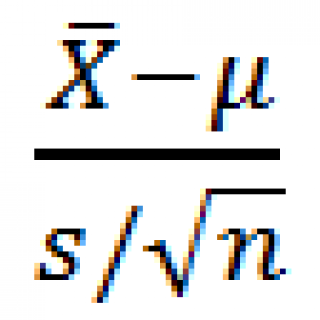
Пусть выборка извлекается из нормального распределения с параметрами N(μ;σ ² ). Рассмотрим статистику 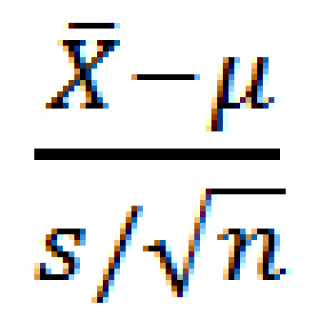, где s – стандартное отклонение выборки , n – размер выборки .

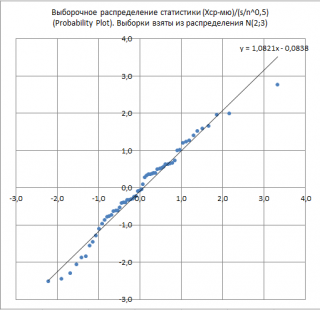
Известно, что выборочное распределение статистики при достаточно большом размере выборки стремится к распределению Стьюдента с n-1 степенью свободы.

Аналогично статистике Х _ср , в файле примера на листе СТЬЮДЕНТ построен График вероятности для проверки этого утверждения.

Использование выборочного распределения вышеуказанной статистики позволяет построить доверительный интервал для оценки математического ожидания при НЕИЗВЕСТНОЙ дисперсии исходного нормального распределения , а также провести проверку соответствующих гипотез .

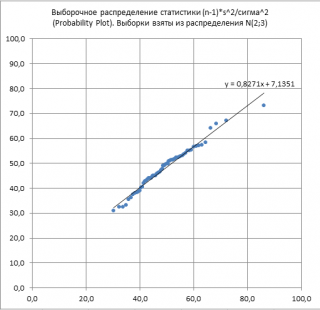
Выборочное распределение статистики (n-1)s ² /σ ²

Пусть выборка извлекается из нормального распределения с параметрами N(μ;σ ² ). Рассмотрим статистику (n-1)s ² /σ ² , где s – стандартное отклонение выборки .

Известно, что Выборочное распределение статистики (n-1)s ² /σ ² при достаточно большом размере выборки стремится к распределению ХИ-квадрат с n-1 степенью свободы.

Аналогично рассмотренной статистике Х _ср , в файле примера на листе ХИ2 построен График вероятности для проверки этого утверждения.

Использование выборочного распределения вышеуказанной статистики позволяет построить доверительный интервал для оценки дисперсии исходного нормального распределения ( из которого берется выборка) , а также провести проверку соответствующих гипотез .

Выборочное распределение статистики

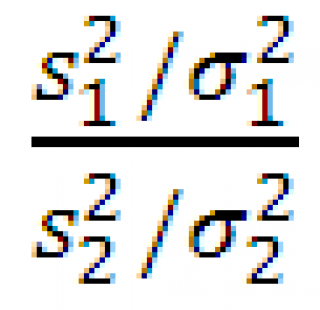
Пусть из двух нормальных распределений с параметрами N(μ ₁ ;σ ₁ ² ) и N(μ ₂ ;σ ₂ ² ) извлекается по одной выборке (в общем случае разного размера n ₁ и n ₂ ) .

Известно, что при достаточно большом размере выборок Выборочное распределение статистики 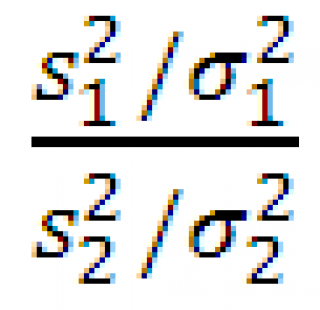стремится к F-распределению вероятности с n ₁ -1 и n ₂ -1 степенями свободы .

F-распределение используется в F-тесте, который сравнивает степени разброса ( дисперсии ) двух наборов данных и при построении соответствующего доверительного интервала .

В файле примера на листе F-расп построен График вероятности для проверки этого утверждения.