Среднее и Математическое ожидание в EXCEL

Вычислим среднее значение выборки и математическое ожидание случайной величины в MS EXCEL.

Выборочное среднее

Среднее выборки или выборочное среднее (sample average, mean) представляет собой среднее арифметическое всех значений выборки .

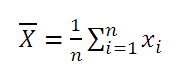
В MS EXCEL для вычисления среднего выборки можно использовать функцию СРЗНАЧ() . В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения выборки .

Выборочное среднее является «хорошей» (несмещенной и эффективной) точечной оценкой математического ожидания случайной величины (см. ниже ), т.е. среднего значения исходного распределения, из которого взята выборка .

Примечание : О вычислении доверительных интервалов при оценке математического ожидания можно прочитать, например, в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL .

Некоторые свойства среднего арифметического :

• Сумма всех отклонений от среднего значения равна 0:

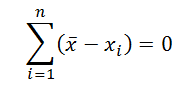
• Если к каждому из значений x _i прибавить одну и туже константу с , то среднее арифметическое увеличится на такую же константу;
• Если каждое из значений x _i умножить на одну и туже константу с , то среднее арифметическое умножится на такую же константу.

Математическое ожидание

Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение . В этом случае среднее значение имеет специальное название - Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.

Примечание : В англоязычной литературе имеется множество терминов для обозначения математического ожидания : expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].

Если случайная величина имеет дискретное распределение , то математическое ожидание вычисляется по формуле:

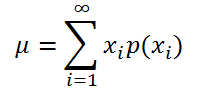
где x _i – значение, которое может принимать случайная величина, а р(x _i ) – вероятность, что случайная величина примет это значение.

Если случайная величина имеет непрерывное распределение , то математическое ожидание вычисляется по формуле:

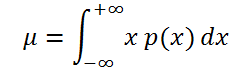
где р(x) – плотность вероятности (именно плотность вероятности , а не вероятность, как в дискретном случае).

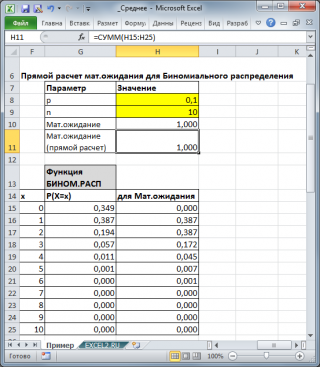
Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения ). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).

Свойства математического ожидания

E[a*X]=a*E[X], где а - const

E[X+a]=E[X]+a

E[a]=a

E[E[X]]=E[X] - т.к. величина E[X] - является const

E[X+Y]=E[X]+E[Y] - работает даже для случайных величин не являющихся независимыми.

СОВЕТ : Про другие показатели распределения - Дисперсию и Стандартное отклонение, можно прочитать в статье Дисперсия и стандартное отклонение в MS EXCEL .