Медиана в EXCEL

Для вычисления медианы в MS EXCEL существует специальная функция МЕДИАНА() . В этой статье дадим определение медианы и научимся вычислять ее для выборки и для заданного закона распределения случайной величины.

Начнем с медианы для выборок (т.е. для фиксированного набора значений).

Медиана выборки

Медиана (median) – это число, которое является серединой множества чисел: половина чисел множества больше, чем медиана , а половина чисел меньше, чем медиана .

Для вычисления медианы необходимо сначала отсортировать множество чисел (значения в выборке ). Например, медианой для выборки (2; 3; 3; 4 ; 5; 7; 10) будет 4. Т.к. всего в выборке 7 значений, три из них меньше, чем 4 (т.е. 2; 3; 3), а три значения больше (т.е. 5; 7; 10).

Если множество содержит четное количество чисел, то вычисляется среднее для двух чисел, находящихся в середине множества. Например, медианой для выборки (2; 3; 3 ; 6 ; 7; 10) будет 4,5, т.к. (3+6)/2=4,5.

Для определения медианы в MS EXCEL существует одноименная функция МЕДИАНА() , английский вариант MEDIAN().

Медиана не обязательно совпадает со средним значением (mean, average) в выборке . Совпадение имеет место только в том случае, если значения в выборке распределены симметрично относительно среднего . Например, для выборки (1; 2; 3 ; 4 ; 5; 6) медиана и среднее равны 3,5.

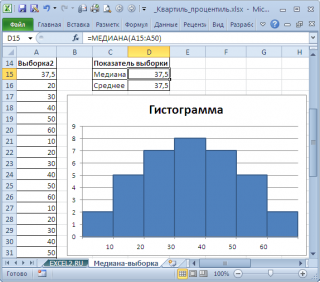
Чтобы в этом убедиться - построим гистограмму для симметричной выборки, состоящую из 36 значений, и вычислим среднее и медиану (см. файл примера лист Медиана-выборка ).

В чем же ценность медианы ? Почему ее используют зачастую наравне со средним значением ?

Оба параметра используются для определения «центральной тенденции» выборки . Для выборки с несимметричным распределением, медиана будет отличаться от среднего . Например, для (1; 2; 3 ; 4 ; 5; 600) медиана равна 3,5, а вот среднее равно 103,5 (смещено в сторону б о льшего значения).

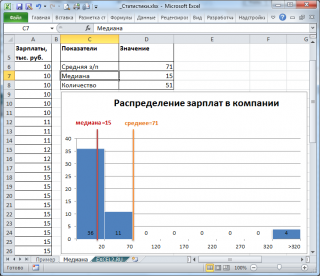
То есть, если имеется длинный хвост распределения, то медиана лучше, чем среднее значение, отражает «типичное» или «центральное» значение. Например, рассмотрим пример несправедливого распределения зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников (также см. статью Описательная статистика , раздел Медиана ).

Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что как минимум у половины сотрудников зарплата меньше или равна 15 тыс. руб.

Примечание : Так как медиана является 50-й процентилью и 2-й квартилью , ее также можно вычислить с помощью формул =ПРОЦЕНТИЛЬ.ВКЛ( Выборка;0,5 ) и =КВАРТИЛЬ.ВКЛ( Выборка;2 ) , где Выборка – это ссылка на диапазон, содержащий значения выборки.

Если выборка содержит нечетное количество чисел, то для вычисления медианы можно также воспользоваться формулой: НАИБОЛЬШИЙ(Выборка;СЧЁТ(Выборка)/2) .

Медиана непрерывного распределения

Если Функция распределения F (х) случайной величины х непрерывна, то медиана является решением уравнения F(х) =0,5.

Примечание : подробнее о Функции распределения см. статью Функция распределения и плотность вероятности в MS EXCEL .

Если известна Функция распределения F(х) или функция плотности вероятности p (х) , то медиану можно найти из уравнения:

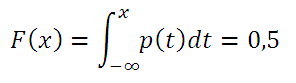
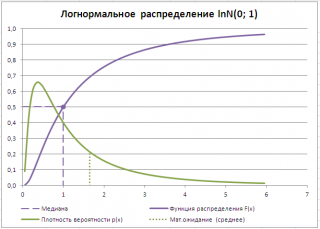
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ ² ), получим, что медиана вычисляется по формуле =EXP(μ). При μ=0, медиана равна 1.

Обратите внимание на точку Функции распределения , для которой F (х)=0,5 (см. картинку выше) . Абсцисса этой точкиравна1. Это и есть значение медианы, что естественно совпадает с ранее вычисленным значением по формуле em.

В MS EXCEL медиану для логнормального распределения LnN(0;1) можно вычислить по формуле =ЛОГНОРМ.ОБР(0,5;0;1) .

Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице.

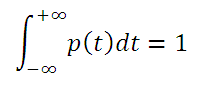
Поэтому, линия медианы (х=Медиана) делит площадь под графиком функции плотности вероятности на две равные части.

Примечание : В статье о распределениях MS EXCEL приведены ссылки на распределения для которых в MS EXCEL существуют специальные функции ( нормальное распределение , гамма-распределение , Экспоненциальное и др.). Используя эти функции можно вычислить медиану соответствующего распределения.