Функция распределения и плотность вероятности в EXCEL

Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL .

Сначала введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия. Затем вычислим плотности вероятности с использованием функций MS EXCEL.

Генеральная совокупность и случайная величина

Приведем несколько определений Генеральной совокупности, чтобы раскрыть более полно ее смысл.

Генеральная совокупность (ГС) - совокупность всех объектов обладающих характеристиками, относительно которых предполагается делать статистические выводы при решении конкретной задачи. Таким образом, ГС определяется конкретной задачей. Например, если нужно предсказать итоги выбора в конкретной стране, то ГС - это все население страны, имеющее право голоса на выборах. Но, если нужно определить как будут голосовать женщины, то, понятно, ГС содержит только женщин, имеющих право голоса.

При ор­га­ни­за­ции вы­бо­роч­но­го об­сле­до­ва­ния генеральной совокупностью на­зы­ва­ют мно­же­ст­во объ­ек­тов, из ко­то­рых про­из­во­дит­ся вы­борка. Например, если станок произвел партию деталей из 1000 шт за 1 смену и нам требуется провести выборочный контроль на основании характеристик 10шт, то ГС в данном случае 1000шт.

В ма­те­ма­тической ста­ти­сти­ке генеральная совокупность яв­ля­ет­ся аб­ст­ракт­ным по­ня­ти­ем, пред­став­ляю­щим со­бой мно­же­ст­во ре­зуль­та­тов всех воз­мож­ных на­блю­де­ний, ко­то­рые мож­но по­лу­чить при дан­ном ком­плек­се ус­ло­вий. Например, если мы бросаем одну монету, то ГС это множество всех исходов, т.е. (Орел; Решка). Если бросаем 2 монеты, то ГС состоит из (ОО; ОР; РО; РР).

Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения генеральная совокупность представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.

Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является случайной величиной . По определению, любая случайная величина имеет функцию распределения , которая обычно обозначается F(x).

Функция распределения

Функцией распределения вероятностей случайной величины Х называют функцию F(x), значение которой в точке х равно вероятности события X < x (вероятность того, что случайная величина Х примет значение меньше х). Математическая запись этого определения выглядит так:

F(x) = P(X < x)

Поясним на примере станка, выпускающего деталь, заданного веса. Очевидно, что веса изготовленных деталей будут слегка отличаться от целевого (на процесс могут воздействать колебания температуры окружающей среды, случайные скачки напряжения, неоднородные свойства материала, стиль работы оператора станка и пр.). Пусть самая тяжелая деталь, произведенная станком, весит 200 г, а самая легкая - 190 г. Вероятность того, что случайно выбранная деталь Х будет весить меньше 201 г равна 1. Вероятность того, что будет весить меньше 190 г равна 0. Промежуточные значения определяются формой Функции распределения. Например, если процесс настроен на изготовление деталей весом 195 г, то разумно предположить, что вероятность выбрать деталь легче 195 г равна 0,5.

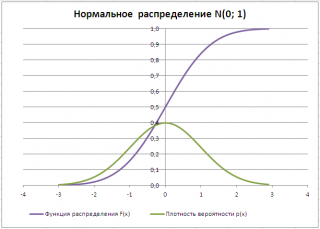
Типичный график Функции распределения для непрерывной случайной величины приведен на картинке ниже (фиолетовая кривая, см. файл примера ):

В справке MS EXCEL Функцию распределения называют Интегральной функцией распределения ( Cumulative Distribution Function , CDF ).

Приведем некоторые свойства Функции распределения:

• Функция распределения F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
• Функция распределения – неубывающая функция;
• Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x ₁ <= X < x ₂ )=F(x ₂ )-F(x ₁ ).

Существует 2 типа распределений: непрерывные распределения и дискретные распределения .

Дискретные распределения

Если случайная величина может принимать только определенные значения и количество таких значений конечно, то соответствующее распределение называется дискретным . Например, при бросании монеты, имеется только 2 элементарных исхода, и, соответственно, случайная величина может принимать только 2 значения. Например, 0 (выпала решка) и 1 (не выпала решка) (см. схему Бернулли ). Если монета симметричная, то вероятность каждого исхода равна 1/2. При бросании кубика случайная величина принимает значения от 1 до 6. Вероятность каждого исхода равна 1/6. Сумма вероятностей всех возможных значений случайной величины равна 1.

Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .

Непрерывные распределения и плотность вероятности

В случае непрерывного распределения случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для непрерывной случайной величины равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой функции плотности распределения p(x) . Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение функции распределения на этом интервале:

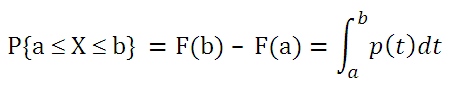
Как видно из формулы выше плотность распределения р(х) представляет собой производную функции распределения F(x), т.е. р(х) = F’(x).

Типичный график функции плотности распределения для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):

Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .

В литературе Функция плотности распределения непрерывной случайной величины может называться: Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF) .

Чтобы все усложнить, термин Распределение (в литературе на английском языке - Probability Distribution Function или просто Distribution ) в зависимости от контекста может относиться как Интегральной функции распределения, так и к ее Плотности распределения.

Из определения функции плотности распределения следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от Функции распределения, больше 1. Например, для непрерывной равномерной величины , распределенной на интервале [0; 0,5] плотность вероятности равна 1/(0,5-0)=2. А для экспоненциального распределения с параметром лямбда =5, значение плотности вероятности в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.

Напомним, что плотность распределения является производной от функции распределения , т.е. «скоростью» ее изменения: p(x)=(F(x ₂ )-F(x ₁ ))/D _x при D _x стремящемся к 0, где D _x =x ₂ -x ₁ . Т.е. тот факт, что плотность распределения >1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере экспоненциального распределения ).

Примечание : Площадь, целиком заключенная под всей кривой, изображающей плотность распределения , равна 1.

Примечание : Напомним, что функцию распределения F(x) называют в функциях MS EXCEL интегральной функцией распределения . Этот термин присутствует в параметрах функций, например в НОРМ.РАСП (x; среднее; стандартное_откл; интегральная ). Если функция MS EXCEL должна вернуть Функцию распределения, то параметр интегральная , д.б. установлен ИСТИНА. Если требуется вычислить плотность вероятности , то параметр интегральная , д.б. ЛОЖЬ.

Примечание : Для дискретного распределения вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL плотность вероятности может называть даже "функция вероятностной меры" (см. функцию БИНОМ.РАСП() ).

Вычисление плотности вероятности с использованием функций MS EXCEL

Понятно, что чтобы вычислить плотность вероятности для определенного значения случайной величины, нужно знать ее распределение, включая параметры.

Найдем плотность вероятности для стандартного нормального распределения N(0;1) при x=2. Для этого необходимо записать формулу =НОРМ.СТ.РАСП(2;ЛОЖЬ) =0,054 или =НОРМ.РАСП(2;0;1;ЛОЖЬ) .

Напомним, что вероятность того, что непрерывная случайная величина примет конкретное значение x равна 0. Для непрерывной случайной величины Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).

Вычисление вероятностей с использованием функций MS EXCEL

1) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению (см. картинку выше), приняла положительное значение. Согласно свойству Функции распределения вероятность равна F(+∞)-F(0)=1-0,5=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу

=НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА)

=1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).

2) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению , приняла отрицательное значение. Согласно определения Функции распределения, вероятность равна F(0)=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу

=НОРМ.СТ.РАСП(0;ИСТИНА)

=0,5.

3) Найдем вероятность того, что случайная величина, распределенная по стандартному нормальному распределению , примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу

=НОРМ.СТ.РАСП(1;ИСТИНА) - НОРМ.СТ.РАСП(0;ИСТИНА)

Все расчеты, приведенные выше, относятся к случайной величине, распределенной по стандартному нормальному закону N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье Распределения случайной величины в MS EXCEL приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.

Обратная функция распределения (Inverse Distribution Function)

Вспомним задачу из предыдущего раздела: Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.

Вероятность этого события равна 0,5.

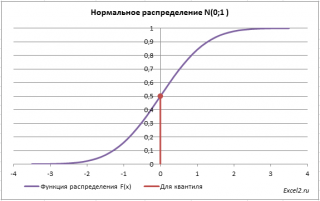
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение меньше x, равна 0,5 (или другими словами вычислим медиану или 50-ю процентиль ).

Для этого необходимо на графике функции распределения найти точку, для которой F(х)=0,5, а затем найти абсциссу этой точки. Абсцисса точки =0, т.е. вероятность, того что случайная величина Х примет значение< 0, равна 0,5.

В MS EXCEL используйте формулу =НОРМ.СТ.ОБР(0,5) =0.

Однозначно вычислить значение случайной величины позволяет свойство монотонности функции распределения.

Обратите внимание, что для вычисления обратной функции мы использовали именно функцию распределения , а не плотность распределения . Поэтому, в аргументах функции НОРМ.СТ.ОБР() отсутствует параметр интегральная , который подразумевается. Подробнее про функцию НОРМ.СТ.ОБР() см. статью про нормальное распределение .

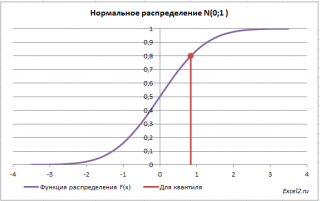
Обратная функция распределения вычисляет квантили распределения , которые используются, например, при построении доверительных интервалов . Т.е. в нашем случае число 0 является 0,5-квантилем нормального распределения . В файле примера можно вычислить и другой квантиль этого распределения. Например, 0,8-квантиль равен 0,84.

В англоязычной литературе обратная функция распределения часто называется как Percent Point Function (PPF).

Примечание : При вычислении квантилей в MS EXCEL используются функции: НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .