Проверка статистических гипотез в EXCEL о равенстве среднего значения распределения (дисперсия известна)

Рассмотрим использование MS EXCEL при проверке статистических гипотез о среднем значении распределения в случае известной дисперсии. Вычислим тестовую статистику Z ₀ , рассмотрим процедуру «одновыборочный z-тест», вычислим Р-значение (Р- value ).

Проверка гипотез (Hypothesis testing) тесно связана с построением доверительных интервалов . При первом знакомстве с процедурой проверки гипотез рекомендуется начать с изучения построения соответствующего доверительного интервала .

СОВЕТ : Для проверки гипотез нам потребуется знание следующих понятий:

• дисперсия и стандартное отклонение ,
• выборочное распределение статистики ,
• уровень доверия/ уровень значимости ,
• стандартное нормальное распределение и его квантили .

Формулировка задачи. Из генеральной совокупности имеющей нормальное распределение с неизвестным μ и известной дисперсией σ ² взята выборка размера n. Необходимо проверить статистическую гипотезу о равенстве неизвестного μ заданному значению μ ₀ (англ. Inference on the mean of a population, variance known).

Примечание : Требование о нормальности исходного распределения, из которого берется выборка , не является строгим. Н ₀ , необходимо, чтобы были выполнены условия применения Центральной предельной теоремы .

Статистическая гипотеза – это некое утверждение о неизвестных параметрах распределения. Процедура проверки гипотез зависит от оцениваемого параметра распределения и условий задачи. Сначала рассмотрим общий подход при проверке гипотез , затем рассмотрим конкретный пример.

Обычно формулируют 2 гипотезы: нулевую Н ₀ и альтернативную Н ₁ . В нашем случае нулевой гипотезой будет равенство μ и μ ₀ , а альтернативной гипотезой – их отличие. Нулевая гипотеза отвергается только в том случае, если на это достаточно оснований. В этом случае принимается альтернативная гипотеза .

Чтобы понять, достаточно ли у нас оснований для отклонения нулевой гипотезы , из распределения делают выборка.

Сначала проведем проверку гипотезы , используя доверительный интервал , а затем с помощью вышеуказанной процедуры z-тест . В конце вычислим Р-значение и также используем его для проверки гипотезы .

Итак, нулевая гипотеза Н ₀ утверждает, что неизвестное среднее значение распределения μ равно μ ₀ . Соответствующая альтернативная гипотеза Н ₁ утверждает обратное: μ не равно μ ₀ . Это пример двусторонней проверки , т.к. неизвестное значение может быть как больше, так и меньше μ ₀ .

Если упрощенно, то проверка гипотезы заключается в сравнении 2-х величин: вычисленного на основании выборки среднего значения Х _ср и заданного μ ₀ . Если эти значения «отличаются больше, чем можно было бы ожидать исходя из случайности», то нулевую гипотезу отклоняют.

Поясним фразу «отличаются больше, чем можно было бы ожидать исходя из случайности». Для этого, вспомним, что распределение Выборочного среднего (статистика Х _ср ) стремится к нормальному распределению со средним значением μ и стандартным отклонением равным σ/√n, где σ – стандартное отклонение распределения , из которого берется выборка (не обязательно нормальное ), а n – объем выборки (подробнее см. статью про ЦПТ ). В нашем случае стандартное отклонение σ известно.

В задачах проверки гипотез также задается уровень доверия (вероятность), который определяет порог между утверждением «мало вероятно» и «вполне вероятно» или «может быть обусловлено случайностью» и «не может быть обусловлено случайностью». Обычно используют значения уровня доверия 90%; 95%; 99%, реже 99,9% и т.д.

Примечание : Уровень доверия равен (1-α) , где α – уровень значимости . И наоборот, α=( 1-уровень доверия ) .

Таким образом, знание распределения статистики Х _ср и заданного уровня доверия , позволяют нам формализовать с помощью математических выражений фразу «отличаются больше, чем можно было бы ожидать исходя из случайности». В этом нам поможет доверительный интервал (как строится доверительный интервал нам известно из этой статьи ).

Если среднее выборки попадает в доверительный интервал, построенный относительно μ ₀ , то для отклонения нулевой гипотезы оснований нет.

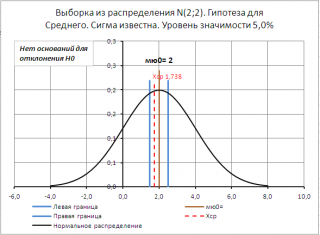
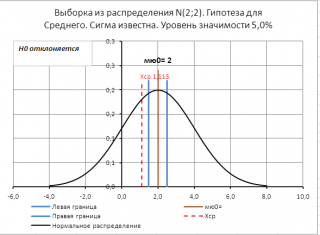
Для визуализации процедуры проверки гипотез в файле примера на листе Сигма известна создана диаграмма .

Если μ ₀ не попадает в доверительный интервал, то нулевая гипотеза отклоняется.

Теперь рассмотрим проверку гипотез с помощью процедуры z -тест .

Z-тест

Кроме доверительного интервала для проверки гипотез существует также и другой эквивалентный подход - z -тест:

• На основе выборки вычисляют тестовую статистику . Выбор тестовой статистики делают в зависимости от оцениваемого параметра распределения и условий задачи. В нашем случае тестовой статистикой является случайная величина z= 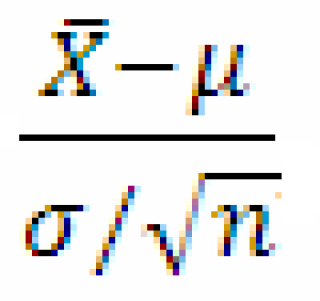, где 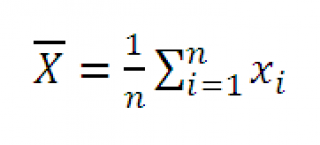– среднее выборки (обозначим Х _ср ). Значение, которое приняла z- статистика , обычно обозначают Z ₀ ;
• z -статистика , как и любая другая случайная величина, имеет свое распределение. В процедуре проверки гипотез это распределение называют « эталонным распределением », англ. Reference distribution. В нашем случае тестовая статистика 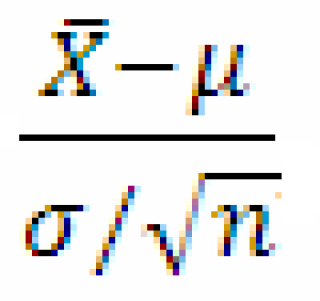имеет стандартное нормальное распределение ;
• Также исследователь устанавливает требуемый уровень значимости – это допустимая для данной задачи ошибка первого рода , т.е. вероятность отклонить нулевую гипотезу , когда она верна ( уровень значимости обозначают буквой α и чаще всего выбирают равным 0,1; 0,05 или 0,01);
• С помощью эталонного распределения для заданного уровня значимости вычисляют соответствующие квантили этого распределения . В нашем случае, при проверке двухсторонней гипотезы , необходимо будет вычислить верхний α/2-квантиль стандартного нормального распределения, т.е. такое значение случайной величины z , что P ( z >= Z _{α /2} )=α/2 ;
• И наконец, значение тестовой статистики Z ₀ сравнивают с вычисленными на предыдущем шаге квантилями и делают статистический вывод : Имеются ли основания, чтобы отвергнуть нулевую гипотезу ? В нашем случае проверки двусторонней гипотезы, Н ₀ отвергается если: |Z ₀ |>Z _{α /2} .

Примечание : Подробнее про квантили распределения можно прочитать в статье Квантили распределений MS EXCEL .

В MS EXCEL верхний α /2-квантиль стандартного нормального распределения вычисляется по формуле =НОРМ.СТ.ОБР(1-α/2)

Учитывая симметричность стандартного нормального распределения относительно оси ординат, верхний α /2-квантиль равен обычному α /2-квантилю со знаком минус: =-НОРМ.СТ.ОБР(α/2)

Примечание : Еще раз подчеркнем связь процедуры z -теста с построением доверительного интервала . Т.к. z -статистика распределена по стандартному нормальному закону, то можно ожидать, что 1-α значений z -статистики будет попадать в интервал между -Z _α/2 и Z _α/2 . Например, для уровня доверия 95% в интервал между -1,960 и 1,960 будет попадать примерно 95% значений Z ₀ , вычисленных на основе выборки . Если Z ₀ не попало в указанный интервал, то это считается маловероятным событием и нулевая гипотеза отвергается.

В случае односторонней гипотезы речь идет об отклонении μ только в одну сторону: либо больше либо меньше μ ₀ . Если альтернативная гипотеза звучит как μ>μ ₀ , то гипотеза Н ₀ отвергается в случае Z ₀ > Z _α . Если альтернативная гипотеза звучит как μ<μ ₀ , то гипотеза Н ₀ отвергается в случае Z ₀ < -Z _α .

Вычисление Р-значения

При проверке гипотез большое распространение также получил еще один эквивалентный подход, основанный на вычислении p -значения (p-value). Поясним его на основе односторонней гипотезы Н ₁ : μ>μ ₀ .

Напомним, что если Н ₁ утверждает, что μ>μ ₀ , то односторонняя гипотеза Н ₀ отвергается в случае если Z ₀ > Z _α . Эти значения z -статистики имеют размерность анализируемой случайной величины, но их трудно интерпретировать. Преобразуем неравенство Z ₀ > Z _α так, чтобы его можно было проще интерпретировать.

Напомним, что Z _α – это положительная величина и она равна верхнему α -квантилю стандартного нормального распределения (такому значению случайной величины z, что P(z>=Z _α )=α). Неравенство Z ₀ > Z _α означает, что если Z ₀ , вычисленное на основе выборки , будет слишком велико, т.е. больше Z _α , то эта ситуация считается маловероятным событием и появляется основание для отклонения нулевой гипотезы .

Поэтому, логично вычислить вероятность события, что z -статистика примет значение z>=Z ₀ и сравнить ее с вероятностью, что z=>Z _α . Вероятность события z=>Z _α (по определению верхнего квантиля ) – это просто α. Вероятность события, что z -статистика примет значение z>=Z ₀ равна 1-Ф(Z ₀ ), где Ф(z) – интегральная функция стандартного нормального распределения . В MS EXCEL эта функция вычисляется по формуле =1-НОРМ.СТ.РАСП(Z ₀ ;ИСТИНА)

Примечание : В MS EXCEL для вычисления p-значения имеется специальная функция Z.TEСT() , которая эквивалентна выражению =1-НОРМ.СТ.РАСП(Z ₀ ;ИСТИНА) . Про функцию Z.TEСT() см. ниже .

Таким образом, неравенство Z ₀ > Z _α эквивалентно неравенству P(z>= Z ₀ )<α или в других обозначениях 1-Ф(Z ₀ )<α. Величина 1-Ф(Z ₀ ) называется p -значением.

СОВЕТ : Лучше понять вышесказанное помогут графики функции стандартного нормального распределения из статьи Квантили распределений MS EXCEL .

Теперь, если p-значение меньше чем заданный уровень значимости α , то нулевая гипотеза отвергается и принимается альтернативная гипотеза . И наоборот, если p-значение больше α, то нулевая гипотеза не отвергается. Другими словами, если p-значение меньше уровня значимости α, то это свидетельство того, что значение z -статистики , вычисленное на основе выборки при условии истинности нулевой гипотезы , приняло маловероятное значение Z ₀ .

Для другой односторонней гипотезы (μ<μ ₀ ) p-значение вычисляется как Ф(Z ₀ ) или =НОРМ.СТ.РАСП(Z ₀ ;ИСТИНА) .  Соответственно, p-значение для односторонней гипотезы μ<μ ₀ вычисляется по формуле =1-Z.TEСT( выборка ; μ ₀ ; σ) , где выборка – ссылка на диапазон, содержащий значения выборки .

В случае двусторонней гипотезы, p -значение вычисляется по формуле =2*(1-Ф(|Z ₀ |)).

В качестве примера проверим гипотезу Н ₀ : μ=μ ₀ , при этом альтернативная односторонняя гипотеза Н ₁ : μ<μ ₀ . Известно, что среднее выборки размера 60 равно 1,851; стандартное отклонение =2; μ ₀ =2,3; уровень значимости равен 0,05. Решение: Z ₀ =(1,851-2,3)/(2/КОРЕНЬ(60))=-1,739 p-значение =НОРМ.СТ.РАСП(-1,739;ИСТИНА)=0,04 Нулевая гипотеза отклоняется, т.к. 0,04<0,05.

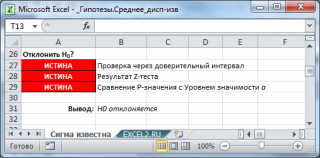
Эквивалентность этих трех подходов для проверки гипотез ( проверка через доверительный интервал , z -тест и p-значение ) продемонстрирована в файле примера : во всех случаях, когда z-тест дает заключение о необходимости отклонить нулевую гипотезу , Х _ср не попадает в соответствующий доверительный интервал, а p -значение меньше уровня значимости.

Функция Z.ТЕСТ()

MS EXCEL для процедуры z-тест существует специальная функция Z.ТЕСТ() , которая на самом деле вычисляет p-значение в случае односторонней альтернативной гипотезы μ >μ ₀ : =Z.TEСT( выборка ; μ ₀ ; σ) , где выборка – ссылка на диапазон, содержащий n значений выборки, σ – известное стандартное отклонение распределения, из которого делается выборка .

Функция Z.ТЕСТ() эквивалентна формуле =1- НОРМ.СТ.РАСП((СРЗНАЧ( выборка )- μ ₀ ) / (σ/√n);ИСТИНА)

Выражение (СРЗНАЧ( выборка )- μ ₀ ) / (σ/√n) – это значение тестовой статистики , т.е. Z ₀ .

Эту же функцию можно использовать для вычисления p -значения в случае проверки двусторонней гипотезы , записав формулу: =2 * МИН(Z.TEСT( выборка ; μ ₀ ; σ); 1 - Z.TEСT( выборка ; μ ₀ ; σ)

Для вычисления p -значения в случае односторонней альтернативной гипотезы μ <μ ₀ используйте формулу: =1-Z.TEСT( выборка ; μ ₀ ; σ)

σ - третий аргумент функции Z.ТЕСТ() должен быть всегда указан, т.к. это соответствует вышерассмотренной процедуре z-теста .