Распределение Фишера (F-распределение). Распределения математической статистики в EXCEL
12 ноября 2016 г.
- Группы статей
- Распределения вероятностей
Рассмотрим распределение Фишера (F-распределение). С помощью функции MS EXCEL F .РАСП() построим графики функции распределения и плотности вероятности, поясним применение этого распределения для целей математической статистики.
F-распределение (англ. F-distribution) применяется для целей дисперсионного анализа (ANOVA), при проверке гипотезы о равенстве дисперсий двух нормальных распределений (F-тест) и др.
Определение : Если U 1 и U 2 независимые случайные величины, имеющие ХИ2-распределение с k 1 и k 2 степенями свободы соответственно, то распределение случайной величины:
носит название F -распределения с параметрами k 1 и k 2 .
Плотность F -распределения выражается формулой:
где Г(…) – гамма-функция:
если альфа – положительное целое, то Г( альфа )=( альфа -1)!
СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
Приведем пример случайной величины, имеющей F -распределение.
Пусть имеется 2 нормальных распределения N(μ 1 ;σ 1 ) и N(μ 2 ; σ 2 ), из которых сделаны выборки размером n 1 и n 2 . Если s 1 2 и s 2 2 – дисперсии этих выборок , то отношение
имеет F -распределение. Это соотношение нам потребуется при проверке гипотезы о равенстве дисперсий двух нормальных распределений (F-тест) .
Графики функций
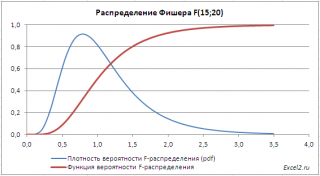
F -распределение при небольших параметрах (<50) имеет несимметричную форму, скошенную вправо (длинный правый хвост).
Среднее значение равно k 2 /(k 2 -2) при k 2 >2, дисперсия равна 2*k 2 2 *(k 1 +k 2 -2)/(k 1 *(k 2 -4)*(k 2 -2) 2 ) при k 2 >4.
В файле примера на листе График приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
F-распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для F-распределения имеется специальная функция F.РАСП() , английское название – F.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и интегральную функцию распределения (вероятность, что случайная величина Х, имеющая F - распределение , примет значение меньше или равное х, P(X <= x)).
Примечание : Плотность вероятности можно также вычислить впрямую, с помощью формул (см. файл примера ).
До MS EXCEL 2010 в EXCEL была функция FРАСП() , которая позволяет вычислить функцию распределения (точнее - правостороннюю вероятность, т.е. P(X>x)). Функция FРАСП() оставлена в MS EXCEL 2010 для совместимости. Аналогом FРАСП() является функция F.РАСП.ПХ() , появившаяся в MS EXCEL 2010.
Примеры расчетов приведены в файле примера на листе Функции .
В MS EXCEL имеется еще одна функция, использующая для расчетов F-распределение – это F.ТЕСТ(массив1;массив2) . Эта функция возвращает результат F-теста : двухстороннюю вероятность того, что разница между дисперсиями выборок "массив1" и "массив2" несущественна. Предполагается, что выборки делаются из нормального распределения .
Подробнее об использовании этой функции см. статью про проверку гипотез о равенстве двух дисперсий .
Обратная функция F-распределения
Обратная функция используется для вычисления альфа - квантилей , т.е. для вычисления значений x при заданной вероятности альфа , причем х должен удовлетворять выражению P{X<=x}= альфа .
В MS EXCEL обратная функция реализована с помощью функции F.ОБР() .
Функция F.ОБР.ПХ() используется для вычисления верхнего квантиля . Т.е. если в качестве аргумента функции указан уровень значимости, например 0,05, то функция вернет такое значение случайной величины х, для которого P(X>x)=0,05. В качестве сравнения: функция F.ОБР() вернет такое значение случайной величины х, для которого P(X<=x)=0,05.
В MS EXCEL 2007 и ранее вместо F.ОБР.ПХ() использовалась функция FРАСПОБР() .
Вышеуказанные функции можно взаимозаменять, т.к. следующие формулы возвращают одинаковый результат: =F.ОБР(0,05;k1;k2) =F.ОБР.ПХ(1-0,05;k1;k2) = FРАСПОБР (1-0,05;k1;k2)
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
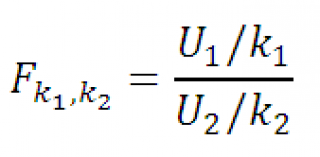
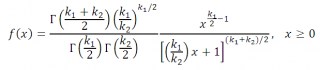
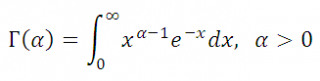
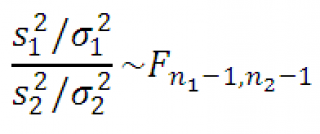
Комментарии