Проверка статистических гипотез в EXCEL о дисперсии нормального распределения
11 декабря 2016 г.
- Группы статей
- Статистический вывод
Рассмотрим использование MS EXCEL при проверке статистических гипотез о дисперсии нормального распределения. Вычислим тестовую статистику χ 2 и Р-значение (Р- value ).
Первое знакомство с процедурой проверки гипотез (Hypothesis testing) для дисперсии рекомендуется начать с изучения построения соответствующего доверительного интервала (см. статью Доверительный интервал для оценки дисперсии в MS EXCEL ).
Примечание : Перечень статей о проверке гипотез приведен в статье Проверка статистических гипотез в MS EXCEL .
СОВЕТ : Для проверки гипотез потребуется знание следующих понятий:
- дисперсия и стандартное отклонение ,
- доверительный интервал для оценки среднего ,
- выборочное распределение статистики ,
- уровень доверия/ уровень значимости ,
- нормальное распределение , распределение χ 2 и их квантили .
Формулировка задачи. Из генеральной совокупности имеющей нормальное распределение с неизвестным средним значением μ (мю) и неизвестной дисперсией σ 2 ( сигма 2 ) взята выборка размера n. Необходимо проверить двустороннюю статистическую гипотезу о равенстве неизвестной дисперсии σ 2 заданному исследователем значению σ 0 2 (англ. Inference on the variance of a normal population).
Примечание : Изложенный ниже метод проверки гипотез о дисперсии ,очень чувствителен к выполнению требования о нормальности распределения , из которого берется выборка . Если это требование не выполняется, то этот метод проверки гипотез будет давать неточные значения.
В качестве точечной оценкой дисперсии распределения, из которого взята выборка , используют Дисперсию выборки s 2 .
Перед процедурой проверки гипотезы , исследователь устанавливает требуемый уровень значимости – это допустимая для данной задачи ошибка первого рода , т.е. вероятность отклонить нулевую гипотезу , когда она верна ( уровень значимости обозначают буквой α (альфа) и чаще всего выбирают равным 0,1; 0,05 или 0,01).
Тестовой статистикой для проверки этой гипотезы является величина:
В статье про χ 2 -распределение показано , что выборочное распределение этой статистики, имеет χ 2 -распределение с n-1 степенью свободы, которое является « эталонным распределением » (англ. Reference distribution) для данного теста о равенстве дисперсии .
Значение, которое приняла χ 2 -статистика обозначим χ 0 2 .
Нулевая гипотеза Н 0 о равенстве дисперсии значению σ 0 2 отвергается в том случае, если χ 0 2 >χ 2 α/2,n-1 или χ 0 2 <χ 2 1-α/2,n-1
где:
- χ 2 α/2,n-1 – верхний α/2-квантиль распределения χ 2 с n -1 степенью свободы (такое значение случайной величины χ 2 n-1 , что P ( χ 2 n-1 >= χ 2 α/2,n-1 )=α/2 ).
- χ 2 1-α/2,n-1 – верхний (1-α/2)-квантиль распределения χ 2 с n -1 степенью свободы (такое значение случайной величины χ 2 n-1 , что P ( χ 2 n-1 >= χ 2 1-α/2,n-1 ) =1-α/2 ).
Примечание : Подробнее про квантили распределения можно прочитать в статье Квантили распределений MS EXCEL .
В MS EXCEL верхний α/2-квантиль распределения χ 2 вычисляется с помощью формулы =ХИ2.ОБР.ПХ(α/2; n-1)
Верхний (1-α /2)-квантиль вычисляется с помощью аналогичной формулы =ХИ2.ОБР.ПХ(1-α/2; n-1)
или через равный ему нижний квантиль
=ХИ2.ОБР(α/2; n-1)
Вычисления приведены в файле примера .
В случае односторонней гипотезы речь идет об отклонении дисперсии только в одну сторону: либо больше либо меньше σ 0 2 . Если альтернативная гипотеза звучит как σ 2 > σ 0 2 , то гипотеза Н 0 отвергается в случае χ 0 2 > χ 2 α ,n-1 . Если альтернативная гипотеза звучит как σ 2 < σ 0 2 , то гипотеза Н 0 отвергается в случае χ 0 2 < χ 2 1-α ,n-1 .
СОВЕТ : О проверке гипотезы о равенстве дисперсий двух нормальных распределений ( F-test ) см. статью Двухвыборочный тест для дисперсии: F-тест в MS EXCEL .
Вычисление Р-значения
При проверке гипотез большое распространение также получил еще один эквивалентный подход, основанный на вычислении p -значения (p-value).
СОВЕТ : Подробно про p -значение написано в статье Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна) .
Если p-значение , вычисленное на основании выборки , меньше чем заданный уровень значимости α , то нулевая гипотеза отвергается и принимается альтернативная гипотеза . И наоборот, если p-значение больше α, то нулевая гипотеза не отвергается.
Формула для вычисления p-значения зависит от формулировки альтернативной гипотезы :
- Для односторонней гипотезы σ 2 < σ 0 2 p-значение вычисляется как =ХИ2.РАСП( χ 0 2 ; n-1;ИСТИНА)
- Для другой односторонней гипотезы σ 2 > σ 0 2 p-значение вычисляется как =ХИ2.РАСП.ПХ( χ 0 2 ; n-1)
- Для двусторонней гипотезы p-значение вычисляется как =2*МИН(ХИ2.РАСП( χ 0 2 ;n-1;ИСТИНА); ХИ2.РАСП.ПХ( χ 0 2 ;n-1))
Соответственно, χ 0 2 = (СЧЁТ( выборка )-1)* ДИСП.В( выборка )/ σ 0 2 , где выборка – ссылка на диапазон, содержащий значения выборки .
СОВЕТ : Подробнее про вышеуказанные функции MS EXCEL см. статью про χ 2 -распределение .
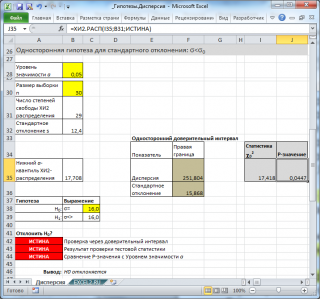
В файле примера на листе Дисперсия показано решение задач проверки двусторонней и односторонних гипотез .
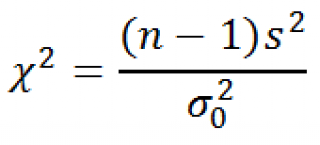
Комментарии