Проверка статистических гипотез в EXCEL о равенстве среднего значения распределения (дисперсия неизвестна)
10 декабря 2016 г.
- Группы статей
- Статистический вывод
Рассмотрим использование MS EXCEL при проверке статистических гипотез о среднем значении распределения в случае неизвестной дисперсии. Вычислим тестовую статистику t 0 , рассмотрим процедуру «одновыборочный t -тест», вычислим Р-значение (Р- value ).
Материал данной статьи является продолжением статьи Проверка статистических гипотез о равенстве среднего значения распределения (дисперсия известна) . В указанной статье даны основные понятия проверки гипотез ( нулевая и альтернативная гипотезы, тестовые статистики, эталонное распределение, Р-значение и др. ).
СОВЕТ : Для проверки гипотез потребуется знание следующих понятий:
- дисперсия и стандартное отклонение ,
- выборочное распределение статистики ,
- стандартная ошибка, Центральная предельная теорема ,
- уровень доверия/ уровень значимости ,
- нормальное распределение , распределение Стьюдента и их квантили .
Формулировка задачи. Из генеральной совокупности имеющей нормальное распределение с неизвестным средним значением μ (мю) и неизвестной дисперсией взята выборка размера n. Необходимо проверить статистическую гипотезу о равенстве неизвестного μ заданному значению μ 0 (англ. Inference on the mean of a population, variance unknown).
Примечание : Требование о нормальности исходного распределения, из которого берется выборка , не является обязательным. Но, необходимо, чтобы были выполнены условия применения Центральной предельной теоремы .
Сначала проведем проверку гипотезы , используя доверительный интервал , а затем с помощью процедуры t -тест. В конце вычислим Р-значение и также используем его для проверки гипотезы .
Пусть нулевая гипотеза Н 0 утверждает, что неизвестное среднее значение распределения μ равно μ 0 . Соответствующая альтернативная гипотеза Н 1 утверждает обратное: μ не равно μ 0 . Это пример двусторонней проверки , т.к. неизвестное значение может быть как больше, так и меньше μ 0 .
Если упрощенно, то проверка гипотезы заключается в сравнении 2-х величин: вычисленного на основании выборки среднего значения Х ср и заданного μ 0 . Если эти значения «отличаются больше, чем можно было бы ожидать исходя из случайности», то нулевую гипотезу отклоняют.
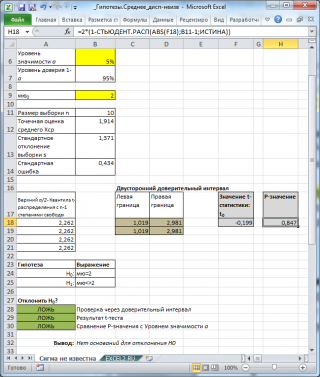
Поясним фразу «отличаются больше, чем можно было бы ожидать исходя из случайности». Для этого, вспомним, что распределение Выборочного среднего (статистика Х ср ) стремится к нормальному распределению со средним значением μ и стандартным отклонением равным σ/√n, где σ – стандартное отклонение распределения, из которого берется выборка (не обязательно нормальное ), а n – объем выборки (подробнее см. статью про ЦПТ ).
К сожалению, в нашем случае дисперсия а, значит, и стандартное отклонение , неизвестны, поэтому вместо нее мы будем использовать ее оценку - дисперсию выборки s 2 и, соответственно, стандартное отклонение выборки s.
Известно, что если вместо неизвестной дисперсии распределения σ 2 мы используем дисперсию выборки s 2 , то распределением статистики Х ср является распределение Стьюдента с n-1 степенью свободы .
Таким образом, знание распределения статистики Х ср и заданного уровня доверия , позволяют нам формализовать с помощью математических выражений фразу «отличаются больше, чем можно было бы ожидать исходя из случайности».
В этом нам поможет доверительный интервал (как строится доверительный интервал нам известно из статьи Доверительный интервал для оценки среднего (дисперсия неизвестна) в MS EXCEL ). Если среднее выборки попадает в доверительный интервал, построенный относительно μ 0 , то для отклонения нулевой гипотезы оснований нет. Если не попадает, то нулевая гипотеза отвергается.
Воспользуемся выражением для Доверительного интервала , которое мы получили в статье Доверительный интервал для оценки среднего (дисперсия неизвестна) .
Напомним, что доверительный интервал обычно определяют через количество стандартных отклонений , которые в нем укладываются. В нашем случае в качестве стандартного отклонения берется стандартная ошибка s/√n.
Количество стандартных отклонений зависит от количества степеней свободы используемого t-распределения и уровня значимости α (альфа) .
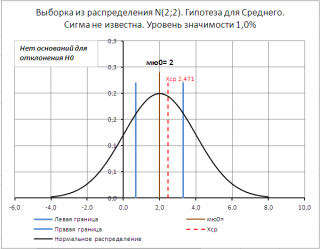
Для визуализации проверки гипотезы методом доверительного интервала в файле примера на листе Сигма неизвестна создана диаграмма .
Примечание : Перечень статей о проверке гипотез приведен в статье Проверка статистических гипотез в MS EXCEL .
t-тест
Ниже приведем процедуру проверки гипотезы в случае неизвестной дисперсии . Данная процедура имеет название t -тест :
- Формулируют 2 гипотезы: нулевую Н 0 и альтернативную Н 1 . В случае формулирования двухсторонней гипотезы , нулевой гипотезой будет равенство μ и μ 0 , а альтернативной гипотезой – их отличие. Нулевая гипотеза отвергается только в том случае, если на это достаточно оснований. В этом случае принимается альтернативная гипотеза ;
- Чтобы понять, достаточно ли у нас оснований для отклонения нулевой гипотезы , из распределения делают выборка.
-
На основе
выборки
вычисляют
тестовую статистику
. В нашем случае
тестовой статистикой
является случайная величина t (
t
-статистика
)
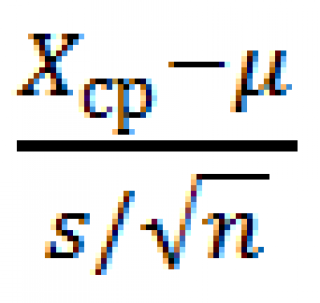 , где
Х
ср
–
среднее выборки
. Значение, которое приняла
тестовая статистика
, обычно обозначают t
0
;
, где
Х
ср
–
среднее выборки
. Значение, которое приняла
тестовая статистика
, обычно обозначают t
0
;
-
Выбранная
тестовая статистика
, как и любая другая случайная величина, имеет свое распределение. В процедуре
проверки гипотез
это распределение называют «
эталонным распределением
», англ. Reference distribution. В нашем случае, когда
дисперсия
неизвестна,
тестовая статистика
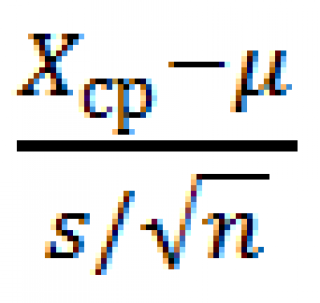 имеет
t-распределение
с n-1
степенью свободы
;
имеет
t-распределение
с n-1
степенью свободы
;
- Также исследователь устанавливает требуемый уровень значимости – это допустимая для данной задачи ошибка первого рода , т.е. вероятность отклонить нулевую гипотезу , когда она верна ( уровень значимости обозначают буквой α и чаще всего выбирают равным 0,1; 0,05 или 0,01);
- С помощью эталонного распределения для заданного уровня значимости вычисляют соответствующие квантили этого распределения . В нашем случае, при проверке двухсторонней гипотезы , необходимо будет вычислить верхний α/2-квантиль t-распределения с n-1 степенью свободы, т.е.такое значение случайной величины t n-1 , что P(t n-1 >=t α /2,n-1 )= α /2 ;
- И, наконец, значение тестовой статистики t 0 сравнивают с вычисленными на предыдущем шаге квантилями и делают статистический вывод : Имеются ли основания, чтобы отвергнуть нулевую гипотезу ? В нашем случае проверки двусторонней гипотезы , Н 0 отвергается если: |t 0 |> t α /2, n-1
В MS EXCEL верхний α /2-квантиль вычисляется по формуле =СТЬЮДЕНТ.ОБР(1- α /2; n-1)
Учитывая симметричность t- распределения относительно оси ординат, верхний α /2-квантиль равен обычному α /2-квантилю со знаком минус: =-СТЬЮДЕНТ.ОБР( α /2; n-1)
Также в MS EXCEL имеется специальная формула для вычисления двухсторонних квантилей : =СТЬЮДЕНТ.ОБР.2Х( α ; n-1) Все три формулы вернут один и тот же результат.
Примечание : Подробнее про квантили распределения можно прочитать в статье Квантили распределений MS EXCEL .
Примечание : Если вместо t- распределения использовать стандартное нормальное распределение, то мы получим необоснованно более узкий доверительный интервал , тем самым мы будем чаще необоснованно отвергать нулевую гипотезу , когда она справедлива ( увеличим ошибку первого рода ).
Отметим, что различие в ширине интервалов зависит от размера выборки n (при уменьшении n различие увеличивается) и от уровня значимости (при уменьшении α различие увеличивается). Для n=10 и α = 0,01 относительная разница в ширине интервалов составляет порядка 20%. При большом размере выборки n (>30), различием в интервалах часто пренебрегают (для n=30 и α = 0,01 относительная разница составляет 6,55%). Это свойство используется в функции Z.ТЕСТ() , которая вычисляет р-значение (см. ниже) с использованием нормального распределения (аргумент σ должен быть опущен или указана ссылка на стандартное отклонение выборки ).
В случае односторонней гипотезы речь идет об отклонении μ только в одну сторону: либо больше либо меньше μ 0 . Если альтернативная гипотеза звучит как μ>μ 0 , то гипотеза Н 0 отвергается в случае t 0 > t α ,n-1 . Если альтернативная гипотеза звучит как μ<μ 0 , то гипотеза Н 0 отвергается в случае t 0 < - t α ,n-1 .
Вычисление Р-значения
При проверке гипотез большое распространение также получил еще один эквивалентный подход, основанный на вычислении p -значения (p-value).
СОВЕТ : Подробнее про p -значение написано в статье Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна) .
Если p-значение , вычисленное на основании выборки , меньше чем заданный уровень значимости α , то нулевая гипотеза отвергается и принимается альтернативная гипотеза . И наоборот, если p-значение больше α , то нулевая гипотеза не отвергается.
Другими словами, если p-значение меньше уровня значимости α , то это свидетельство того, что значение t -статистики , вычисленное на основе выборки при условии истинности нулевой гипотезы , приняло маловероятное значение t 0 .
Формула для вычисления p-значения зависит от формулировки альтернативной гипотезы :
- Для односторонней гипотезы μ<μ 0 p-значение вычисляется как =СТЬЮДЕНТ.РАСП(t 0 ; n-1; ИСТИНА)
- Для другой односторонней гипотезы μ>μ 0 p-значение вычисляется как =1-СТЬЮДЕНТ.РАСП(t 0 ; n-1; ИСТИНА)
- Для двусторонней гипотезы p-значение вычисляется как =2*(1-СТЬЮДЕНТ.РАСП(ABS(t 0 );n-1;ИСТИНА))
Соответственно, t 0 =(СРЗНАЧ( выборка )-μ 0 )/ (СТАНДОТКЛОН.В( выборка )/ КОРЕНЬ(СЧЁТ( выборка ))) , где выборка – ссылка на диапазон, содержащий значения выборки .
В файле примера на листе Сигма неизвестна показана эквивалентность проверки гипотезы через доверительный интервал , статистику t 0 ( t -тест) и p -значение .
Примечание : В MS EXCEL нет специализированной функции для одновыборочного t-теста . При больших n можно использовать функцию Z.ТЕСТ() с опущенным 3-м аргументом (подробнее про эту функцию см. статью Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна) ). Функция СТЬЮДЕНТ.ТЕСТ() предназначена для двухвыборочного t-теста .
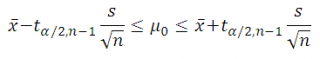
Комментарии