Доверительный интервал для оценки среднего (дисперсия неизвестна) в EXCEL

Построим доверительный интервал для оценки среднего значения генеральной совокупности в случае неизвестного значения дисперсии.

Материал данной статьи является продолжением статьи Доверительный интервал для оценки среднего (дисперсия известна) .

СОВЕТ : Для построения Доверительного интервала нам потребуется знание следующих понятий:

• дисперсия и стандартное отклонение ,
• выборочное распределение статистики ,
• стандартная ошибка ,
• уровень доверия/ уровень значимости ,
• нормальное распределение , распределение Стьюдента и его квантили .

Формулировка задачи. Предположим, что из генеральной совокупности имеющей нормальное (или приблизительно нормальное ) распределение взята выборка размера n. Предполагается, что стандартное отклонение σ (или дисперсия σ ² ) этого распределения неизвестно. Необходимо на основании этой выборки оценить неизвестное среднее значение распределения (μ, математическое ожидание ) и построить двухсторонний доверительный интервал .

Т.к. в этой задаче стандартное отклонение не известно, то вместо σ нужно использовать его оценку – стандартное отклонение выборки s, и, соответственно, вместо стандартного отклонения выборочного среднего использовать стандартную ошибку =s/КОРЕНЬ(n) .

Напомним, что в вышеуказанной статье про доверительный интервал при известном стандартном отклонении , для вычисления вероятностей мы использовали статистику Хср (среднее выборки) , которая, согласно ЦПТ , имеет нормальное или приблизительно нормальное распределение . Нам был известен один из его параметров: стандартное отклонение =σ/КОРЕНЬ(n) . Доверительный интервал рассчитывался относительно точечной оценки - Хср .

Если стандартное отклонение неизвестно, то для построения доверительного интервала вместо статистики Хср необходимо использовать статистику .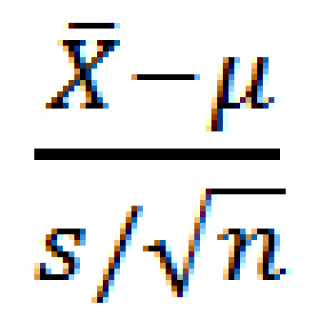

Как было показано в статье Статистики, выборочное распределение и точечные оценки в MS EXCEL выборочное распределение статистики 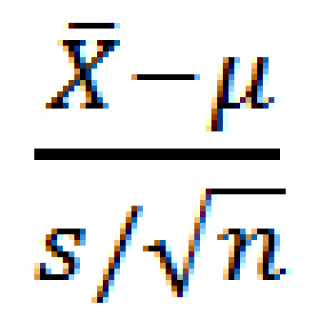будет стремиться к распределению Стьюдента с n-1 степенью свободы, где n – размер выборки .

Вспомним вероятностное утверждение, которое мы использовали для формирования доверительного интервала в случае с известным σ: «Вероятность того, что среднее генеральной совокупности находится в пределах 1,960 « стандартных отклонений выборочного среднего» от среднего выборки , равна 95%».

Примечание : Значение вероятности, упомянутое в утверждении, имеет специальное название уровень доверия , который связан с уровнем значимости α простым выражением Уровень доверия = 1 - α . В нашем случае уровень значимости α =1-0,95=0,05 .

Значение 1,960 – это верхний квантиль стандартного нормального распределения, соответствующий уровню значимости 5% (1-95%) . В нашем случае его нужно заменить на верхний (двухсторонний) квантиль распределения Стьюдента с n-1 степенью свободы t _α/2,n-1 .

Чтобы вычислить этот квантиль в MS EXCEL необходимо записать формулу =СТЬЮДЕНТ.ОБР.2Х(0,05;n-1) или =СТЬЮДЕНТ.ОБР(1-0,05/2; n-1) или =-СТЬЮДЕНТ.ОБР(0,05/2; n-1)

При одном и том же уровне значимости, t-распределение будет давать более широкий доверительный интервал, чем стандартное нормальное распределение, т.к. у нас теперь меньше информации из-за того, что вместо σ мы использовали ее оценку s.

Теперь запишем соответствующую формулу для определения двухстороннего доверительного интервала :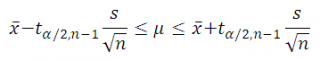

где t _α/2,n-1 – верхний α /2-квантиль распределения Стьюдента ( такое значение случайной величины t _n-1 , что P (t _n-1 > =t _α/2,n-1 )= α /2) .

Примечание : Верхний α/2-квантиль определяет ширину доверительного интервала в стандартных ошибках. Верхний α /2- квантиль распределения Стьюдента всегда больше 0, что очень удобно. Обычно при построении доверительных интервалов для оценки среднего используют только верхний α /2- квантиль и не используют нижний α /2- квантиль .

Это возможно потому, что распределение Стьюдента симметрично относительно оси х ( плотность его распределения симметрична относительно среднего, т.е. 0 ) . Поэтому,нет нужды вычислять нижний α /2-квантиль (его называют просто α /2-квантиль ), т.к. он равен верхнему α /2- квантилю со знаком минус.

Примечание : Более подробно про t-распределение Стьюдента см. статью Распределение Стьюдента (t-распределение). Распределения математической статистики в MS EXCEL .

В файле примера на листе Сигма неизвестна создана форма для расчета и построения двухстороннего доверительного интервала .

СОВЕТ : О построении других доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .

Функция ДОВЕРИТ.СТЬЮДЕНТ()

Если значения выборки находятся в диапазоне B20:B79 , а уровень значимости равен 0,05; то формула MS EXCEL: =СРЗНАЧ(B20:B79)- ДОВЕРИТ.СТЬЮДЕНТ(0,05; СТАНДОТКЛОН.В(B20:B79); СЧЁТ(B20:B79)) вернет левую границу доверительного интервала .

Эту же границу можно вычислить с помощью формулы: =СРЗНАЧ(B20:B79)- СТЬЮДЕНТ.ОБР(1-0,05/2; СЧЁТ(B20:B79)-1)* СТАНДОТКЛОН.В(B20:B79)/ КОРЕНЬ(СЧЁТ(B20:B79))

Примечание : Функция ДОВЕРИТ.СТЬЮДЕНТ() появилась в MS EXCEL 2010.