Доверительный интервал для оценки дисперсии в EXCEL
27 ноября 2016 г.
- Группы статей
- Статистический вывод
Построим доверительный интервал для оценки дисперсии случайной величины, распределенной по нормальному закону, в MS EXCEL .
Построение доверительного интервала для оценки среднего приведено в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL . Процедура построения доверительного интервала для оценки дисперсии имеет много общего с процедурой для оценки среднего , поэтому в этой статье она изложена менее подробно, чем в указанной статье.
Формулировка задачи. Предположим, что из генеральной совокупности имеющей нормальное распределение с неизвестным средним значением μ и неизвестной дисперсией σ 2 взята выборка размера n. Необходимо на основании этой выборки оценить дисперсию распределения и построить доверительный интервал .
Примечание : Построение доверительного интервала для оценки среднего относительно нечувствительно к отклонению генеральной совокупности от нормального закона . А вот при построении доверительного интервала для оценки дисперсии требование нормальности является строгим.
СОВЕТ : Для построения Доверительного интервала нам потребуется знание следующих понятий:
- дисперсия и стандартное отклонение ,
- доверительный интервал для оценки среднего ,
- выборочное распределение статистики ,
- уровень доверия/ уровень значимости ,
- нормальное распределение и распределение ХИ-квадрат .
В качестве точечной оценкой дисперсии распределения, из которого взята выборка , используют Дисперсию выборки s 2 .
Также, перед процедурой проверки гипотезы , исследователь устанавливает требуемый уровень значимости – это допустимая для данной задачи ошибка первого рода , т.е. вероятность отклонить нулевую гипотезу , когда она верна ( уровень значимости обозначают буквой α (альфа) и чаще всего выбирают равным 0,1; 0,05 или 0,01)
В статье про ХИ2-распределение показано, что выборочное распределение статистики y=(n-1) s 2 /σ 2 , имеет ХИ2-распределение с n-1 степенью свободы.
Воспользуемся этим свойством и построим двухсторонний доверительный интервал для оценки дисперсии :
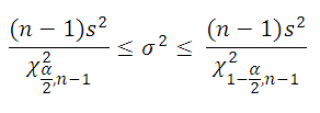 где χ 2 α/2,n-1 – верхний α/2-квантиль распределения ХИ-квадрат с n -1 степенью свободы ( такое значение случайной величины χ 2 n-1 , что P ( χ 2 n-1 >= χ 2 α/2,n-1 )=α/2) . Чтобы найти этот квантиль в MS EXCEL используйте формулу =ХИ2.ОБР.ПХ(α; n-1) . χ 2 1-α/2,n-1 – верхний 1-α/2-квантиль , который равен нижнему α/2- квантилю. Чтобы найти этот квантиль в MS EXCEL используйте формулу =ХИ2.ОБР(α; n-1) .
где χ 2 α/2,n-1 – верхний α/2-квантиль распределения ХИ-квадрат с n -1 степенью свободы ( такое значение случайной величины χ 2 n-1 , что P ( χ 2 n-1 >= χ 2 α/2,n-1 )=α/2) . Чтобы найти этот квантиль в MS EXCEL используйте формулу =ХИ2.ОБР.ПХ(α; n-1) . χ 2 1-α/2,n-1 – верхний 1-α/2-квантиль , который равен нижнему α/2- квантилю. Чтобы найти этот квантиль в MS EXCEL используйте формулу =ХИ2.ОБР(α; n-1) .
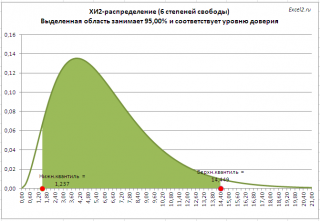
Примечание : В файле примера на листе Квантили показан расчет квантилей для распределения ХИ2 . На рисунке выделена область соответствующая уровню доверия 95%, которая ограничена верхним и нижним квантилем . Обратите внимание, что в отличие от нормального и t-распределения распределение ХИ2 несимметрично, поэтому для двустороннего доверительного интервала потребуется вычислить два квантиля , значения которых будут отличаться.
Примечание : Доверительный интервал для стандартного отклонения может быть получен путем извлечения квадратного корня из вышеуказанного выражения.
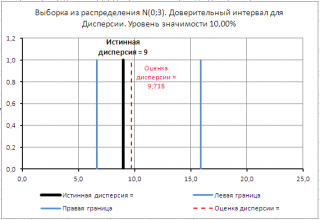
В файле примера на листе 2х сторонний создана форма для расчета и построения двухстороннего доверительного интервала .
Для построения односторонних доверительных интервалов используйте нижеследующие выражения:
Задача
В следующей задаче найдем верхний односторонний доверительный интервал для дисперсии .
Автоматический аппарат заполняет емкости с растворителем. Предполагается, что объемы налитой жидкости в емкостях распределены по нормальному закону . Если разброс значений объемов будет слишком велик, то значительная часть емкостей будет существенно переполнена или не заполнена. Для оценки дисперсии в качестве выборки взято 20 наполненных жидкостью емкостей. На основе выборки была вычислена дисперсия выборки s 2 , которая составила 0,0153 (литров 2 ). Принято решение оценить верхний уровень дисперсии с уровнем доверия 95%.
Для решения задачи воспользуемся выражением
Сначала найдем верхний (1-α)-квантиль (или равный ему нижний α-квантиль ) ХИ2-распределения с n-1 степенью свободы при у ровне значимости α равном 1-0,95=0,05. Это можно сделать в MS EXCEL по формулам: =ХИ2.ОБР.ПХ(1-0,05; 20-1) или =ХИ2.ОБР(0,05; 20-1)
В результате получим верхний доверительный интервал для дисперсии: σ 2 <=0,0287
Или тоже, но словами и для стандартного отклонения: «Значения выборки показывают, что с вероятностью 95%, стандартное отклонение процесса наполнения емкости растворителем меньше или равно 0,17 литров».
Ход решения приведен в файле примера на листе 1 сторонний .
СОВЕТ : О построении других доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .
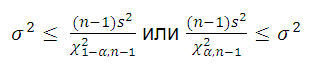
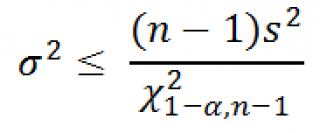
Комментарии