Множественная регрессия в EXCEL
26 января 2019 г.
- Группы статей
- Статистический анализ
Рассмотрим использование MS EXCEL для прогнозирования переменной Y на основании нескольких переменных Х, т.е. множественную регрессию.
Перед прочтением этой статьи рекомендуется освежить в памяти простую линейную регрессию – прогнозирование на основе значений только одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Множественного регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Множественный регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
- Оценка неизвестных параметров
- Диаграмма рассеяния
- Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов
- Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
- Проверка гипотез
- Генерация данных для множественной регрессии с помощью заданного тренда
- Коэффициент детерминации
Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется множественной регрессией .
Множественная линейная регрессионная модель (Multiple Linear Regression Model) имеет вид Y=β 0 +β 1 *X 1 +β 2 *X 2 +…+β k *X k +ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е. регрессоров . ε - случайная ошибка . Модель является линейной относительно неизвестных параметров β.
Оценка неизвестных параметров
В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.
Для описания зависимости Y от 2-х переменных линейная модель имеет вид:
Y=β 0 +β 1 *X 1 +β 2 *X 2 +ε.
Параметры этой модели β i нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β 0 , β 1 , β 2 ) обычно вычисляются методом наименьших квадратов (МНК) , который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).
Соответствующие оценки параметров будем обозначать как b 0 , b 1 и b 2 .
Ошибка ε имеет случайную природу и имеет свою функцию распределения со средним значением =0 и дисперсией σ 2 .
Оценки b 1 и b 2 называются коэффициентами регрессии , они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются неизменными .
Сдвиг (intercept) или постоянный член b 0 , определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто сдвиг не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями МНК ).
Вычислив оценки, полученные методом МНК, позволяют прогнозировать значения переменной Y:
Y= b 0 + b 1 *X 1 + b 2 *X 2
Примечание : Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в плоскости регрессии ).
В качестве примера рассмотрим технологический процесс изготовления нити:
Инженер, на основе имеющегося опыта, предположил, что прочность нити Y зависит от концентрации исходного раствора (Х 1 ) и температуры реакции (Х 2 ), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.
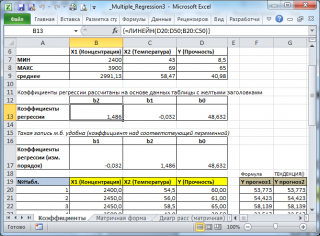
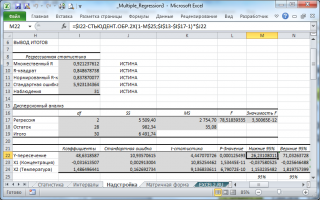
В MS EXCEL коэффициенты множественной регрессии удобнее всего вычислить с помощью функции ЛИНЕЙН() . Это сделано в файле примера на листе Коэффициенты . Чтобы вычислить оценки:
- выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2 коэффициента регрессии + величина сдвига = 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон С8:Е8 ;
- в Строке формул введите = ЛИНЕЙН(D20:D50;B20:C50) . Предполагается, что в столбце В содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах С и D содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D).
- нажмите CTRL + SHIFT + ENTER (т.к. это формула массива ).
В левой ячейке будет рассчитано значение коэффициента регрессии b 2 для переменной Х2, в средней ячейке - значение коэффициента регрессии b 1 для переменной Х1, в правой – сдвиг . Обратите внимание, что порядок вывода коэффициентов регрессии обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент b 2 располагается левее по отношению к b 1 , тогда как значения переменной Х2 располагаются правее значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17 файла примера .
Примечание
: В принципе без функции
ЛИНЕЙН()
можно обойтись, записав альтернативные формулы. Для этого в
файле примера на листе Коэффициенты
в столбцах
I
:
K
вычислены отклонения значений переменных Х
1i
, Х
2i
, Y
i
от их средних значений
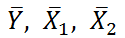 , т.е.:
, т.е.:
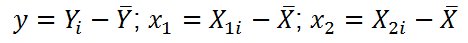
Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):
При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления коэффициентов регрессии значительно усложняются, поэтому следует использовать матричный подход.
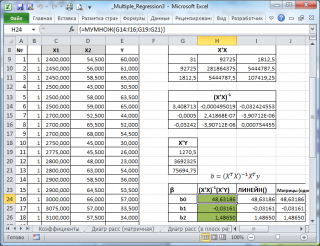
В файле примера на листе Матричная форма выполнены расчеты коэффициентов регрессии с помощью матричного подхода.
Расчет можно произвести как пошагово, так и одной формулой массива :
=МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B9:D33);(B9:D33)));МУМНОЖ(ТРАНСП(B9:D33);(E9:E33)))
Коэффициенты регрессии (вектор b ) в этом случае вычисляются по формуле b =(X T X) -1 (X T Y) или в другом виде записи b =(X ’ X) -1 (X ’ Y)
Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.
Символ Т или ‘ – это транспонирование матрицы , а обозначение -1 говорит о вычислении обратной матрицы .
Диаграмма рассеяния
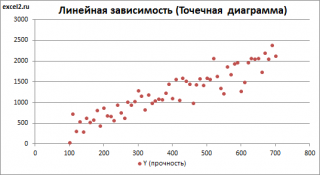
В случае простой линейной регрессии (один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят диаграмму рассеяния (двумерную).
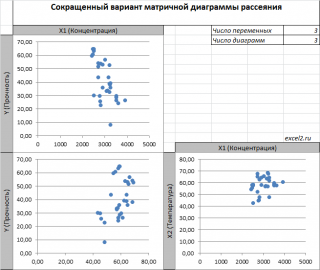
В случае множественной линейной регрессии двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См. файл примера лист Диагр расс (матричная) ).
К сожалению, такую диаграмму трудно интерпретировать.
Более того, матричная диаграмма может вводить в заблуждение (см. Introduction to linear regression analysis / D . C . Montgomery , E . A . Peck , G . G . Vining , раздел 3.2.5 ), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X i и Y.
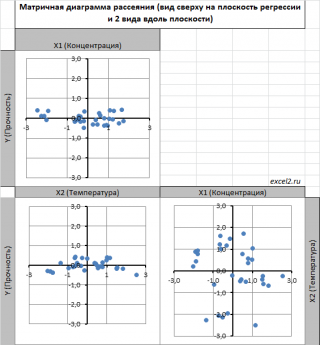
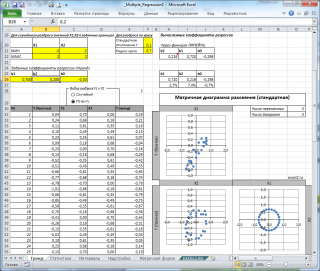
Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной диаграммы рассеяния . В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно плоскости регрессии , то картину, на мой взгляд, будет проще интерпретировать.
Сравним две матричные диаграммы рассеяния (см. файл примера на листе «Диагр расс (в плоск регрессии)» , построенные для одних и тех же наблюдений. Первая – стандартная,
вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.
На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно провести процедуру F-теста ).
Несколько слов о построении альтернативной матричной диаграммы рассеяния:
- Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть среднее и разделить на стандартное отклонение ). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со стандартным нормальным распределением , 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);
- Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти матрицу вращения , например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);
- Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках Q 31: S 31 ).
Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов
После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.
Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:
Y= b 0 + b 1 * Х 1 + b 2 * Х 2
Примечание: В MS EXCEL прогнозное значение Y для заданных Х 1 и Х 2 можно также предсказать с помощью функции ТЕНДЕНЦИЯ() . При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х 1 и Х 2 , а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х 1i и Х 2i ) для выбранного наблюдения i (см. файл примера, лист Коэффициенты, столбец G ). Функция ПРЕДСКАЗ() , использованная нами в простой регрессии, не работает в случае множественной регрессии .
Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить доверительный интервал этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.
Доверительные интервалы построим при фиксированном Х для:
- нового наблюдения Y;
- среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)
Как и в случае простой линейной регрессии , для построения доверительных интервалов нам потребуется сначала вычислить стандартную ошибку модели (standard error of the model) , которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.
Для вычисления стандартной ошибки оценивают дисперсию ошибки ε, т.е. сигма^2 (ее часто обозначают как MS Е либо MSres ) . Затем, вычислив из полученной оценки квадратный корень, получим Стандартную ошибку регрессии (часто обозначают как SEy или sey ).
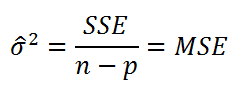
где SSE – сумма квадратов значений ошибок модели ei=yi - ŷi ( Sum of Squared Errors ). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).
Величина n-p – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае простой множественной регрессии с 2-мя регрессорами число степеней свободы равно n-3, т.к. при построении плоскости регрессии было оценено 3 параметра модели b (т.е. на это было «потрачено» 3 степени свободы ).
В MS EXCEL стандартную ошибку SEy можно вычислить формулы (см. файл примера, лист Статистика ):
= ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);3;2)
Стандартная ошибка нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:
x i - вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
где α (альфа) – уровень значимости (обычно принимают равным 0,05=5%)
р – количество оцениваемых параметров модели (в нашем случае = 3)
n-p – число степеней свободы
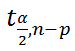 –
квантиль
распределения Стьюдента
(задает количество
стандартных ошибок
, в +/- диапазоне которых вероятность обнаружить новое наблюдение равно 1-альфа). Т.е. если
квантиль
равен 2, то диапазон шириной +/- 2
стандартных ошибок
относительно прогнозного значения Y будет с вероятностью 95% содержать новое наблюдение Y (для каждого заданного Хi). В MS EXCEL вычисления квантиля производят по формуле =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
, подробнее см.
в статье про распределение Стьюдента
.
–
квантиль
распределения Стьюдента
(задает количество
стандартных ошибок
, в +/- диапазоне которых вероятность обнаружить новое наблюдение равно 1-альфа). Т.е. если
квантиль
равен 2, то диапазон шириной +/- 2
стандартных ошибок
относительно прогнозного значения Y будет с вероятностью 95% содержать новое наблюдение Y (для каждого заданного Хi). В MS EXCEL вычисления квантиля производят по формуле =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
, подробнее см.
в статье про распределение Стьюдента
.
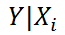 – прогнозное значение Yi вычисляемое по формуле Yi=
b
0+
b
1*
Х1i+
b
2*
Х2i (точечная оценка).
– прогнозное значение Yi вычисляемое по формуле Yi=
b
0+
b
1*
Х1i+
b
2*
Х2i (точечная оценка).
Стандартная ошибка среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:
x i - вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.
Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
В разделе Оценка неизвестных параметров мы получили точечные оценки коэффициентов регрессии . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ) коэффициентов регрессии .
Стандартная ошибка коэффициента регрессии b j (обозначается se ( b j ) ) вычисляется на основании стандартной ошибки по следующей формуле:
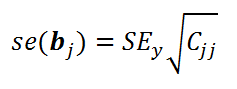
где C jj является диагональным элементом матрицы (X ’ X) -1 . Для коэффициента сдвига b 0 индекс j=1 (верхний левый элемент), для b 1 индекс j=2, b 2 индекс j=3 (нижний правый элемент).
SEy – стандартная ошибка регрессии (см. выше ).
В MS EXCEL стандартные ошибки коэффициентов регрессии можно вычислить с помощью функции ЛИНЕЙН() :
= ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);2;j)
Примечание : Подробнее о функции ЛИНЕЙН() см. статью Функция MS EXCEL ЛИНЕЙН() .
Применяя матричный подход стандартные ошибки можно вычислить и через обычные формулы (точнее через формулу массива , см. файл примера лист Статистика ):
= КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
b j +/- t*Se( b j )
где t – это t-значение , которое можно вычислить с помощью формулы = СТЬЮДЕНТ.ОБР.2Х(0,05;n-p) для уровня значимости 0,05.
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии b j . Здесь мы считаем, что коэффициент регрессии b j имеет распределение Стьюдента с n-p степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Проверка гипотез
Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X, возможен, когда все коэффициенты регрессии β равны 0.
Чтобы убедиться, что вычисленная нами оценка коэффициентов регрессии не обусловлена лишь случайностью (они не случайно отличны от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы Н 1 принимают, что ХОТЯ БЫ ОДИН коэффициент β <>0.
Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением дисперсионного анализа , использованного нами в случае простой линейной регрессии (F-тест) .
Если нулевая гипотеза справедлива, то тестовая F -статистика имеет F-распределение со степенями свободы k и n - k -1 , т.е. F k, n-k-1 :
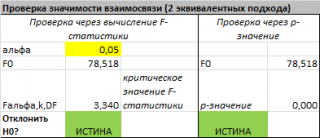
Проверку значимости регрессии можно также осуществить через вычисление p -значения . В этом случае вычисляют вероятность того, что случайная величина F примет значение F 0 (это и есть p-значение ), затем сравнивают p-значение с заданным уровнем значимости α (альфа) . Если p-значение больше уровня значимости , то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL значение F 0 можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции ЛИНЕЙН() :
= ИНДЕКС(ЛИНЕЙН(E13:E43; C13:D43;;ИСТИНА);4;1)
В MS EXCEL для проверки гипотезы через p -значение используйте формулу =F.РАСП.ПХ(F 0 ;k;n-k-1)< альфа
Если формула вернет ИСТИНА, то регрессия значима. Если формула вернет ЛОЖЬ, то у нас нет оснований отклонить нулевую гипотезу, т.е. «скорее всего» все коэффициенты регрессии равны 0 (см. файл примера лист Статистика , где показано эквивалентность обоих подходов проверки значимости регрессии).
В MS EXCEL критическое значение для заданного уровня значимости F 1-альфа, k, n-k-1 можно вычислить по формуле = F.ОБР(1- альфа;k;n-k-1) или = F.ОБР.ПХ(альфа;k; n-k-1) . Другими словами требуется вычислить верхний альфа- квантиль F -распределения с соответствующими степенями свободы .
Таким образом, при значении статистики F 0 > F 1-альфа, k, n-k-1 мы имеем основание для отклонения нулевой гипотезы.
В программах статистики результаты процедуры F -теста выводят с помощью стандартной таблицы дисперсионного анализа . В файле примера такая таблица приведена на листе Надстройка , которая построена на основе результатов, возвращаемых инструментом Регрессия надстройки Пакета анализа MS EXCEL .
Генерация данных для множественной регрессии с помощью заданного тренда
Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.
Для решения этой задачи нам потребуется:
- задать значения регрессоров в нужном диапазоне (значения переменных Х);
- задать коэффициенты регрессии ( b );
- задать тренд (вычислить значения Y= b 0 + b 1 * Х 1 + b 2 * Х 2 );
- задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)
Все вычисления выполнены в файле примера, лист Тренд для случая 2-х регрессоров. Там же построены диаграммы рассеяния .
Коэффициент детерминации
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью ( SSR ) / Общая изменчивость ( SST ).
Этот показатель можно вычислить с помощью функции ЛИНЕЙН() :
= ИНДЕКС(ЛИНЕЙН(E13:E43;C13:D43;;ИСТИНА);3)
При добавлении в модель новой объясняющей переменной Х, коэффициент детерминации будет всегда расти. Поэтому, рост коэффициента детерминации не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.
Более подходящей статистикой, которая лишена указанного недостатка, является нормированный коэффициент детерминации (Adjusted R-squared):
где p – число независимых регрессоров (вычисления см. файл примера лист Статистика ).
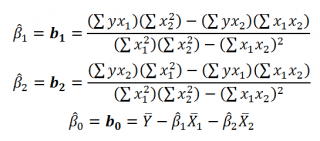

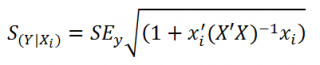
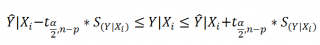
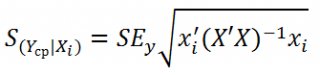
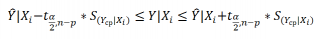
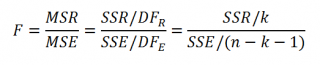
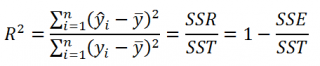
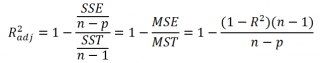
Комментарии