Функция EXCEL ЛИНЕЙН()

Функция ЛИНЕЙН() специально создана для оценки параметров линейной регрессии, а также для вывода регрессионной статистики (коэффициента детерминации, стандартных ошибок, F -статистики и др.).

Функция ЛИНЕЙН() может использоваться для простой регрессии (в этом случае прогнозируемая переменная Y зависит от одной контролируемой переменной Х) и для множественной регрессии (Y зависит от нескольких Х).

Рассмотрим функцию на примере простой регрессии (оценивается наклон и сдвиг линии регрессии). Использование функции в случае множественной регрессии рассмотрено в соответствующей статье про множественную регрессию .

Функция ЛИНЕЙН() возвращает несколько значений, поэтому для вывода результатов потребуется несколько ячеек. Часто функцию вводят как формулу массива : нажатием клавиш CTRL + SHIFT + ENTER , но, как будет показано ниже, для вывода результатов вычислений это не обязательно.

Функция работает в 2-х режимах. В простейшем случае, когда 4-й аргумент функции опущен или установлен ЛОЖЬ, функция возвращает только 2 значения - это оценки параметров модели: наклона a и сдвига b.

Для того, чтобы вычислить оценки:

• выделите 2 ячейки в одной строке,
• в Строке формул введите, например, = ЛИНЕЙН(C23:C83;B23:B83)
• нажмите CTRL + SHIFT + ENTER .

В левой ячейке будет рассчитано значение наклона , в правой – сдвига .

Примечание : В справке MS EXCEL результат функции ЛИНЕЙН() соответствующий наклону обозначается буквой m, а сдвиг – буквой b.

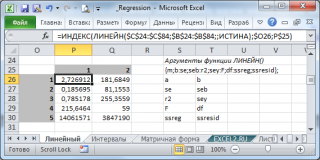
Примечание : Без формул массива можно обойтись. Для этого нужно использовать функцию ИНДЕКС() , которая выведет нужное значение. Например, чтобы вывести величину сдвига линии регрессии введите формулу = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1;2) . Если 4-й аргумент функции опущен или установлен ЛОЖЬ, то функция ЛИНЕЙН() в возвращает массив значений вида 1х2 (т.е. 2 ячейки, расположенные в одной строке). Поэтому, для вывода величины сдвига прямой линии регрессии, первый аргумент функции ИНДЕКС() , который является номером строки, должен быть равен 1, а второй аргумент, номер столбца, должен быть равен 2. Чтобы вывести значение наклона линии регрессии формулу =ЛИНЕЙН(C23:C83;B23:B83) достаточно ввести просто как обычную формулу и нажать ENTER . Конечно, можно использовать и формулу =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1;1) .

Теперь о втором, более сложном режиме функции. Этот режим нужно использовать, если требуется вывести дополнительную статистику (4-й аргумент функции должен быть установлен ИСТИНА). В этом случае функция ЛИНЕЙН() возвращает 10 значений в диапазоне 5х2 ячеек (5 строк и 2 столбца). Как и в более простом режиме, в первой строке возвращаются оценки параметров модели: наклона и сдвига .

Чтобы ввести функцию как формулу массива выполните следующие действия:

• выделите диапазон 5х2 ячеек (2 столбца и 5 строк),
• в Строке формул введите формулу ЛИНЕЙН($C$23:$C$83;$B$23:$B$83;;ИСТИНА)
• чтобы ввести формулу нажмите одновременно комбинацию клавиш CTRL + SHIFT + ENTER

Примечание : Чтобы обойтись без формул массива нужно использовать функцию ИНДЕКС() , которая выведет нужное значение. Например, чтобы вывести коэффициент детерминации R ² введите формулу = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;1) . 3 – это номер строки диапазона 5х2, а 1 – это номер столбца. В файле примера на листе Линейный в диапазоне Q 26: R 30 показано как вывести все значения, возвращаемые функцией ЛИНЕЙН() без формул массива .

Итак, установив 4-й аргумент равным ИСТИНА и введя функцию тем или иным способом, функция выведет:

• в строке 1: оценки параметров модели (наклон и сдвиг).
• в строке 2: Стандартные ошибки для наклона и сдвига . Ошибки обозначаются se и seb;
• в строке 3: коэффициент детерминации и стандартную ошибку регрессии . Обозначаются R ² и SEy;
• в строке 4: значение F-статистики и число степеней свободы . Обозначаются F и df;
• в строке 5: Суммы квадратов SSR, SSE определяющие изменчивость объясненную и необъясненную моделью (см. в статье Простая линейная регрессия разделы про коэффициент детерминации и статью про F-тест ). В справке MS EXCEL SSR, SSE обозначаются как ssreg (Regression Sum of Squares) и ssresid (Residuals Sum of Squares) соответственно.

Примечание : Разобраться в значениях, возвращаемых функцией ЛИНЕЙН() , можно лишь разобравшись в теории линейной регрессии.

В файле примера также приведены формулы, позволяющие сделать расчеты без функции ЛИНЕЙН() – см. диапазон Q 34: R 38 . Альтернативные формулы помогают разобраться в алгоритме расчета вышеуказанных статистических показателей.