Однофакторный дисперсионный анализ (one-way ANOVA) в EXCEL
26 января 2019 г.
- Группы статей
- Статистический анализ
Пусть имеется случайная переменная Y , значения которой мы можем измерять. Исследователь предполагает, что эта переменная зависит от фактора, значения которого мы можем контролировать, т.е. задавать с требуемой точностью. Покажем как методом дисперсионного анализа ( ANOVA ) проверить гипотезу о наличии или отсутствии влияния указанного фактора на зависимую переменную Y .
Disclaimer : Эта статья – о применении MS EXCEL для целей Дисперсионного анализа, поэтому данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения теории Дисперсионного анализа – плохая идея. Хорошая идея - найти в этой статье формулы MS EXCEL для проведения Дисперсионного анализа.
Перед прочтением этой статьи рекомендуется освежить в памяти следующие понятия статистики:
- Проверка статистических гипотез ;
- Дисперсия и среднее значение ;
- Распределение Фишера и квантили этот распределения;
- F-тест ;
- Блочные диаграммы .
Дисперсионный анализ (ANOVA, ANalysis Of VAriance) позволяет проверить гипотезу о равенстве нескольких средних значений выборок (взяты ли выборки из одного распределения или из разных распределений).
Примечание : В статье Двухвыборочный t-тест с одинаковыми дисперсиями решалась подобная задача о сравнении средних значений 2-х распределений. Здесь рассмотрим более общую задачу – будем одновременно сравнивать несколько средних значений выборок (более 2-х).
Чтобы пояснить суть дисперсионного анализа приведем пример.
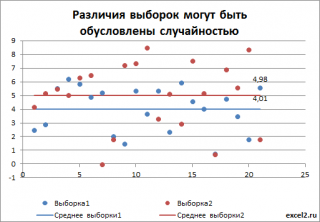
Сгенерируем 2 выборки: первую возьмем из нормального распределения со средним значением равно 4, вторую со средним - 5 ( стандартные отклонения одинаковые). Сказать, сильно ли они различаются или нет, невозможно, пока мы не знаем разброс (стандартное отклонение) значений в каждой выборке относительно среднего. Если зададим в распределениях небольшой разброс, скажем 0,1, то в каждой выборке получим близкое к нему значение. В этом случае, очевидно, что наблюдаемое различие между средними равное 1 (5-4=1) – значительное и можно говорить, что выборки взяты из разных распределений (см. картинку ниже).
Если же разброс в выборках составляет около 2, то наблюжаемое различие средних значений выборок равное 1 уже не кажется таким значительным.
В дисперсионном анализе эти значения выборок представляют собой значения зависимой переменной Y, а выборки берутся при различных уровнях фактора Х. В первом случае для того дать ответ о зависимости Y от фактора Х, даже не нужно проводить дисперсионный анализ : из диаграммы итак очевидно, что отличие между средними значениями выборок (5-4=1), гораздо больше разброса внутри выборки (0,1). Следовательно, очевидно, что выборки взяты из различных генеральных совокупностей (с различными распределениями), которые соответствуют разным значениям Х.
Во втором случае без дисперсионного анализа не обойтись. Различие между средними значениями может быть обусловлено просто случайностью выборок, взятых из одного распределения.
В конце статьи мы определим математически точно условие «значимости» различия средних выборок .
Немного теории
Примечание : Пользователи, уверенно владеющие методом дисперсионного анализа , могут перейти непосредственно к формулам MS EXCEL .
Пусть необходимо исследовать зависимость некой количественной случайной величины Y от одной переменной, которую мы можем контролировать (устанавливать их значения с требуемой точностью). В теории дисперсионного анализа переменная Y называется зависимой переменной ( dependent или response variable ), а переменные, от которых исследуется зависимость переменной Y, называются факторами или зависимыми переменными ( factors или dependent variables ).
Для целей этой статьи будем предполагать, что Y зависит только от одного фактора.
Примечание : Случай зависимости от 2-х факторов рассмотрен в статье Двухфакторный дисперсионный анализ .
Отдельные, заданные значения фактора называются уровнями ( levels ) или испытаниями ( treatments ).
Так как мы можем контролировать значения, которые принимает фактор , то данные (набор значений Y), которые получены в результате испытаний, мы назовем экспериментальными , а сам процесс получения этих данных - экспериментом .
Целью эксперимента является исследование влияния различных уровней фактора на переменную Y. В самом деле, так как фактор нами контролируется, то у нас есть возможность сделать несколько наблюдений (измерений) величины Y при определенном заданном уровне фактора. Зачем их делать несколько, ведь значения Y должны получиться одинаковыми? Нет. Так как мы предполагаем, что на переменную Y может влиять множество неконтролируемых нами факторов, то мы будем получать в ходе каждого измерения несколько отличающиеся значения Y. Единственное, что мы можем сделать, это обеспечить одинаковые условия проведения эксперимента для всех измерений.
Например, измеряя расход бензина на 100 км/ч одной и той же марки бензина на одном и том же автомобиле, мы будем получать несколько различные значения. Может непредсказуемо измениться направление ветра, состояние дороги или автомобиля, что в свою очередь повлияет на расход.
Уровни фактора (treatments) будем обозначать буквой j (j изменяется от 1 до a ). Каждому уровню фактора соответствует одна выборка (состоит из нескольких измерений). Предполагается, что дисперсии всех выборок σ 2 неизвестны, но равны между собой.
Непосредственно измеренные значения Y при заданном уровне фактора j будем обозначать y ij . Количество наблюдений для разных уровней факторов может быть одинаковым или отличаться.
Примечание : Чем больше количество измерений/наблюдений (т.е. размер выборки) мы сделаем, тем более обоснованным будет наш статистический вывод о равенстве средних значений этих выборок.
В тексте статьи будем рассматривать только равные выборки, их размер обозначим n. В Этом случае общее количество измерений N=n*a.
Примечание : В файле примера выполнены вычисления для обоих случаев (равные и неравные по размеру выборки).
Если фактор действительно оказывает влияние на зависимую переменную Y, то при различных уровнях фактора мы должны в среднем получать различные значения Y. Другими словами, мы должны получить «заметно различающиеся» средние выборок при различных уровнях фактора:
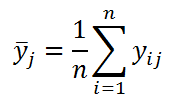
Остается выяснить, что значит средние выборок «заметно отличаются».
Стандартные обозначения дисперсионного анализа
Общий подход при проведении Дисперсионного анализа: проверить значимость различия средних значений выборок, сравнив один источник разброса (проверяемый фактор) с другим источником разброса (обоснованный лишь случайностью выборок/ случайным воздействием неконтролируемых факторов):
Введя нижеуказанные обозначения, выражение можно записать в компактной форме:
SST=SSA+SSE
Эти общеупотребительные обозначения расшифровываются следующим образом: SS – это сокращение английского выражения Sum of Squares (сумма квадратов отклонений от среднего), T – это сокращение от Total (Общее среднее), А – это фактор А, E – это сокращение от Error (ошибка).
На основании данных определений, вышеуказанное выражение может быть преобразовано в вычислительную форму:
где,
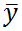 – общее среднее:
– общее среднее:
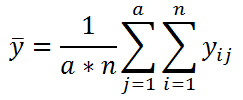
Обратите внимание, что квадраты отклонений имеют размерность дисперсии , т.е. меры изменчивости. Теперь очевидно, что левая часть выражения представляет собой общую изменчивость (разброс) каждого из наблюдений относительно общего среднего. Эта общая изменчивость (SST) состоит из двух частей: SSA - изменчивость, объясненная нашей моделью (междувыборочная изменчивость, основанная на различиях в уровнях фактора) и из SSE - ошибка модели (внутривыборочная изменчивость, сумма разбросов наблюдений внутри каждой выборки).
Также в дисперсионном анализе используется понятие среднего квадрата отклонений (Mean Square), т.е. MS. Соответственно для SST имеем MST=SST/(N-1), для SSA имеем MSA=SSA/(n-1), для ошибки модели SSE имеем MSE=SSE/(a(n-1)).
MS имеет смысл средней изменчивости на 1 наблюдение (с некоторой поправкой). Эта поправка отражает тот факт, что MS должна вычисляться не делением SS на соответствующее количество наблюдений, а на число степеней свободы (degrees of freedom, DF). Например, чтобы вычислить MST, мы из N (общего количества наблюдений) должны вычесть 1, т.к. в выражении SST присутствует одно среднее значение (аналогично тому, как мы делали при вычислении дисперсии выборки ). Одна степень свободы теряется при вычислении среднего – это видно в формуле выражения для SST.
В SSA мы имеем уже а средних значений (равно количеству уровней фактора, т.е. количеству выборок). Поэтому, из общего количества наблюдений a *n необходимо вычесть а – количество вычисленных средний значений выборок (an-a=a(n-1)).
Напомним, что в дисперсионном анализе проверяется гипотеза о равенстве средних значений этих выборок. Т.е. формулируется нулевая гипотеза Н 0 , которая утверждает, что Y не зависит от фактора и все выборки, измеренные при различных уровнях фактора, на самом деле взяты из одного распределения с общим средним.
Идем дальше. Оказывается, если нулевая справедлива , то:
- случайная величина MSА представляет собой оценку σ 2
- отношение MSА/MSE имеет распределение Фишера с а-1 и a ( n -1) степенями свободы.
MSА/MSE обозначают как F 0 ( тестовая статистика для однофакторного дисперсионного анализа ).
Примечание : Можно показать, что MSE также представляет собой оценку σ 2 дисперсии выборок ( математическое ожидание случайной величины MSE равно σ 2 ). Но, в отличие от MSА, MSE представляет собой оценку σ 2 вне зависимости от того, справедлива ли нулевая справедлива или нет.
Теперь, введя основные понятия, рассмотрим вычислительную часть дисперсионного анализа на примере решения задачи.
Задача
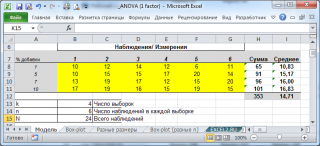
В качестве задачи рассмотрим технологический процесс изготовления нити в химическом реакторе.
Пусть предполагается, что инженер исследует влияние некой добавки на прочность нити Y. Он решает провести эксперимент:
- Использовать 4 различных концентраций добавки (1%; 5%; 7% и 10%). Прим .: эти значения концентраций не участвуют в расчетах.
- Провести по 6 (n) измерений прочности нити для каждой концентрации добавки.
Таким образом, имеется только 1 фактор (концентрация добавки). Фактор имеет 4 (а=4) различные уровня (j=1; 2; 3; 4). Всего у нас имеется 24 (N=4*6) измерения.
Вроде бы эксперимент полностью описан, теперь инженеру требуется только провести измерения. Однако, есть еще одна сложность: на разброс результатов при различных уровнях фактора может повлиять то, как мы проводим эксперимент.
О рандомизированном эксперименте
Представим, что у нас есть только 1 реактор. Инженер включает реактор, делает 6 измерений для первого уровня, затем, для 2-го и т.д. В итоге, может случиться так, что первые 6 измерений у нас будут выполнены в реакторе, который только начал прогреваться, а последние 6, когда он полностью вышел в рабочий режим. Понятно, что такой подход не годится: на разброс выборок может влиять не только концентрация добавки, но и порядок, в котором проводились измерения.
Также не годится подход, когда используются 4 одинаковых, но отдельных реактора для каждого эксперимента: первый реактор для концентрации 1%, второй - для 5% и т.д. Однако, индивидуальные особенности каждого реактора (период эксплуатации, воздействие ремонтов, незначительное различие конструкции допущенное при изготовлении) могут сказаться на разбросе выборки.
То есть для постановки правильного эксперимента требуется исключить влияние конкретного устройства (experimental unit) на значение переменной Y.
Обычно используют полностью рандомизированный эксперимент (completely randomized experimental design) – это когда для каждого испытания ( treatment ) выбираются образцы экспериментального устройства выбираются случайным способом.
Например, для нашего случая можно предложить следующую схему полностью рандомизированного эксперимента : мы случайным образом выбираем из большого количества одинаковых ректоров (например, из 1000) 6 ректоров для наблюдений первого уровня фактора (для каждого наблюдения 1 реактор), 6 – для второго и т.д. Всего 24 ректора из 1000.
Или можно предложить схему попроще. Всего имеется 24 одинаковых реакторов. Для каждого наблюдения выбираем случайным образом свой реактор.
Или еще проще: каждому из 24 измерений случайным образом (вне зависимости от уровня фактора) назначаем один из 4 одинаковых реакторов. Каждый реактор участвует в 6 измерениях.
Примечание : Т.к. не всегда представляется возможным иметь в распоряжении множество одинаковых экспериментальных устройств для проведения полностью рандомизированного эксперимента , то в статистике часто используются и другие формы проведения экспериментов, например, блочный рандомизированный эксперимент ( randomized block design ).
Вычисления в MS EXCEL
Итак, предположим, что все измерения проведены в соответствии со схемой полностью рандомизированного эксперимент а. Результаты измерений представлены в таблице ниже (см. файл примера на листе Модель ).
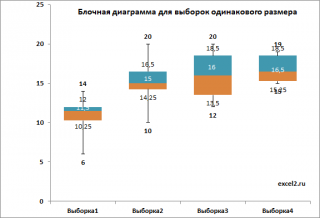
Сначала изучим статистические характеристики набора данных, построив блочную диаграмму .
Из блочной диаграммы видно, что концентрация добавки влияет на прочность нити Y (чем выше концентрация, тем в среднем прочнее нить). Однако, мы пока не можем сделать статистически обоснованный вывод, о том что концентрация добавки влияет на прочность нити . Возможно, различие в средних значениях выборок обусловлено лишь случайностью выборок.
Примечание : Из блочной диаграммы видно, что разброс данных (его отражает дисперсия выборки) имеет примерно одинаковую величину для всех 4-х выборок, что является обязательным условием для корректности применения метода дисперсионного анализа .
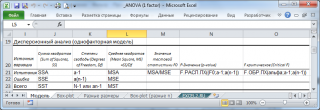
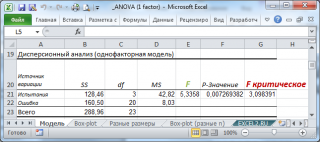
Сделаем вспомогательные вычисления по формулам из предыдущего раздела статьи: вычислим средние значения каждой выборки, общее среднее, суммы квадратов SS, степени свободы, MSE, MSA.
Тестовая статистика вычисляется по формуле:
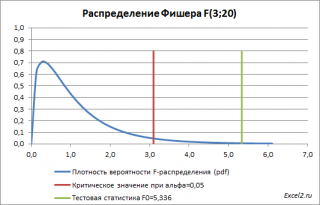
Т.к. тестовая статистика имеет F -распределение ( распределение Фишера ) , то ее значение, вычисленное на основании наблюдений, должно лежать около среднего значения F -распределения с соответствующими степенями свободы .
В нашем случае среднее значение F -распределения с 3 и 20 степенями свободы равно 1,11. Если вычисленное нами значение F 0 «значительно» превосходит это значение, то это является маловероятным событием и у нас есть основания для отклонения нулевой гипотезы .
В нашей задаче F 0 равно 5,3358. «Значительно» это или нет? Для ответа на этот вопрос вычислим вероятность этого события (т.е. вероятность события, что случайная величина F, имеющая распределение Фишера с указанными степенями свободы, примет значение 5,3358 или более). Эта вероятность не высока =0,0072. Этого и следовало ожидать, т.к. 5,3358 значительно больше среднего значения 1,11. В MS EXCEL эту вероятность можно вычислить по формуле:
= F.РАСП.ПХ((F 0 ;a-1;a(n-1))=F.РАСП.ПХ((5,3358;3;20)
0,0072 – это так называемое p -значение , т.е. вероятность, что статистика F 0 примет вычисленное значение.
Примечание : Обычно под F 0 понимается как сама случайная величина - тестовая статистика F 0 , так и ее конкретное значение F 0 , вычисленное из условий задачи (исходных данных).
Теперь сравним p -значение с уровнем значимости (обычно 0,05 или 0,01). Если p -значение меньше уровня значимости , то нулевую гипотезу отклоняют.
В начале статьи мы задались вопросом о том, как математически точно определить «значимое» отличие средних значений выборок (чтобы мы могли сделать вывод, что уровни фактора влияют на значение переменной Y). Теперь мы можем утверждать, что средние выборок статистически значимо отличаются, если вычисленное p -значение меньше заданного уровня значимости .
Таким образом, наша модель является полезной и наше предположение о зависимости Y (прочности нити) от фактора (концентрации добавки) является статистически обоснованным.
Примечание : Однофакторный дисперсионный анализ можно также выполнить с помощью надстройки Пакет анализа . Об этом см. в статье здесь .


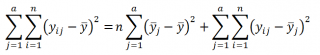
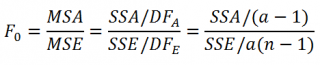
Комментарии