Проверка значимости регрессии с помощью дисперсионного анализа (F-тест)
26 января 2019 г.
- Группы статей
- Статистический анализ
Проведем проверку значимости простой линейной регрессии с помощью процедуры F -тест.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
- проверка гипотезы о равенстве 0 коэффициента регрессии , т.е. наклона;
- проверка статистической значимости коэффициента корреляции ;
- с использованием дисперсионного анализа (процедура F -тест ).
Процедуру F -теста рассмотрим на примере простой линейной регрессии , когда прогнозируемая переменная Y зависит только от одной переменной Х.
Чтобы определить может ли предложенная модель линейной регрессии быть использована для адекватного описания значений переменной Y, дисперсию наблюдаемых данных анализируют методом Дисперсионного анализа (ANOVA for Simple Regression) . Дисперсия данных разбивается на компоненты, которые затем используются в F -тесте для определения значимости регрессии.
F -тест для проверки значимости регрессии НЕ относится к простым и интуитивно понятным процедурам. Вероятно, это связано с тем, что для проведения F -теста требуется быть знакомым с определенным количеством статистических понятий и нужно неплохо разбираться в связанных с ними статистических методах. Нам потребуются понятия из следующих разделов статистики:
- регрессионный анализ ;
- процедура проверки гипотез ;
- статистики и выборочные распределения ;
- распределение Фишера ;
- уровень значимости .
Можно, конечно, рассмотреть F -тест формально:
- вычислить на основании выборки значение тестовой F статистики;
- сравнить полученное значение со значением, соответствующему заданному уровню значимости ;
- в зависимости от соотношения этих величин принять решение о значимости вычисленной линейной регрессии
В этой статье ставится более амбициозная задача – разобраться в самом подходе, на котором основан F -тест . Сначала введем несколько определений, которые используются в процедуре F -теста , затем рассмотрим саму процедуру.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части .
Определения, необходимые для F -теста
Согласно определению дисперсии , дисперсия выборки прогнозируемой переменной Y определяется формулой:
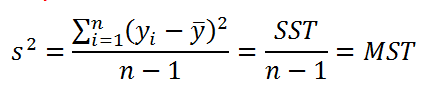
В формуле используется ряд сокращений:
- SST (Total Sum of Squares) – это просто компактное обозначение Суммы Квадратов отклонений от среднего (такое сокращение часто используется в зарубежной литературе).
- MST (Total Mean Square) – Среднее Суммы Квадратов отклонений (еще одно общеупотребительное сокращение).
Примечание : Необходимо иметь в виду, что с одной стороны величины MST и SST являются случайными величинами, вычисленными на основании выборки, т.е. статистиками . Однако с другой стороны, при проведении регрессионного анализа по данным имеющейся выборки вычисляются их конкретные значения. В этом случае величины MST и SST являются просто числами.
Значение n-1 в вышеуказанной формуле равно
числу степеней свободы (
DF
)
, которое относится к
дисперсии выборки
(одна
степень свободы
у
n
величин yi потеряна в результате наличия ограничения
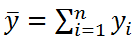 , связывающего все значения выборки). Число
степеней свободы
у величины SST также имеет специальное обозначение: DFT (DF Total).
, связывающего все значения выборки). Число
степеней свободы
у величины SST также имеет специальное обозначение: DFT (DF Total).
Как видно из формулы, отношение величин SST и DFT обозначается как MST. Эти 3 величины обычно выдаются в таблице результатов дисперсионного анализа в различных прикладных статистических программах (в том числе и в надстройке Пакет анализа, инструмент Регрессия ).
Значение SST, характеризующую общую изменчивость переменной Y, можно разбить на 2 компоненты:
- Изменчивость объясненную моделью (Explained variation), обозначается SSR
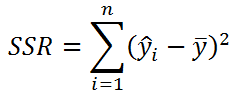
- Необъясненную изменчивость (Unexplained variation), обозначается SSЕ
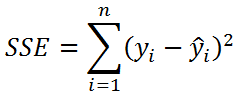
Известно , что справедливо равенство:
SST = SSR + SSE
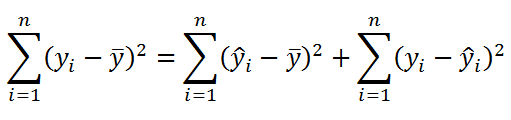
Величинам SSR и SSE также сопоставлены степени свободы . У SSR одна степень свободы , т.к. она однозначно определяется одним параметром – наклоном линии регрессии a (напомним, что мы рассматриваем простую линейную регрессию ). Это очевидно из формулы:
Примечание: Очевидность наличия только одной степени свободы проистекает из факта, что переменная Х – контролируемая (не является случайной величиной).
Число степеней свободы величины SSR имеет специальное обозначение: DFR (для простой регрессии DFR=1, т.к. число независимых переменных Х равно 1) . По аналогии с MST, отношение этих величин также часто обозначают MSR = SSR / DFR .
У SSE число степеней свободы равно n -2 , которое обозначается как DFE (или DFRES - residual degrees of freedom). Двойка вычитается, т.к. изменчивость переменной yi имеет 2 ограничения, связанные с оценкой 2-х параметров линейной модели ( а и b ): ŷi=a*xi+b
Отношение этих величин также часто обозначают MSE = SSE / DFE .
MSR и MSE имеют размерность дисперсий, хотя корректней их называть средними значениями квадратов отклонений. Тем не менее, ниже мы их будем «дисперсиями», т.к. они отображают меру разброса: MSE – меру разброса точек наблюдений относительно линии регрессии, MSR показывает насколько линия регрессии совпадает с горизонтальной линией среднего значения Y.
Примечание : Напомним, что MSE (Mean Square of Errors) является оценкой дисперсии s 2 ошибки, подробнее см. статью про линейную регрессию , раздел Стандартная ошибка регрессии .
Число степеней свободы обладает свойством аддитивности: DFT = DFR + DFE . В этом можно убедиться, составив соответствующее равенство n -1=1+( n -2)
Наконец, определившись с определениями, переходим к рассмотрению самой процедуры F -тест .
Процедура F -теста
Сущность F -теста при проверке значимости регрессии заключается в том, чтобы сравнить 2 дисперсии : объясненную моделью (MSR) и необъясненную (MSE). Если эти дисперсии «примерно равны», то регрессия незначима (построенная модель не позволяет объяснить поведение прогнозируемой Y в зависимости от значений переменной Х). Если дисперсия, объясненная моделью (MSR) «существенно больше», чем необъясненная, то регрессия значимая .
Примечание : Чтобы быстрее разобраться с процедурой F -теста рекомендуется вспомнить процедуру проверки статистических гипотез о равенстве дисперсий 2-х нормальных распределений (т.е. двухвыборочный F-тест для дисперсий ).
Чтобы пояснить вышесказанное изобразим на диаграммах рассеяния 2 случая:
- регрессия значима (в этом случае имеем значительный наклон прямой) и
- регрессия незначима (линия регрессии близка к горизонтальной прямой).
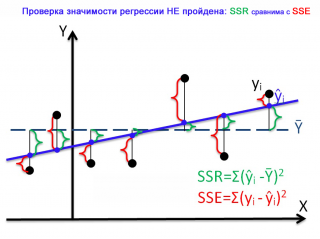
На первой диаграмме показан случай, когда регрессия значима:
- Зеленым цветом выделены расстояния от среднего значения до линии регрессии , вычисленные для каждого хi. Сумма квадратов этих расстояний равна SSR;
- Красным цветом выделены расстояния от линии регрессии до соответствующих точек наблюдений . Сумма квадратов этих расстояний равна SSЕ.
Из диаграммы видно, что в случае значимой регрессии, сумма квадратов «зеленых» расстояний, гораздо больше суммы квадратов «красных». Понятно, что их отношение будет гораздо больше 1. Следовательно, и отношение дисперсий MSR и MSE будет гораздо больше 1 (не забываем, что SSE нужно разделить еще на соответствующее количество степеней свободы n-2).
В случае значимой регрессии точки наблюдений будут находиться вдоль линии регрессии. Их разброс вокруг этой линии описываются ошибками регрессии, которые были минимизированы посредством процедуры МНК . Очевидно, что разброс точек относительно линии регрессии значительно меньше, чем относительно горизонтальной линии, соответствующей среднему значению Y.
Совершенно другую картину мы можем наблюдать в случае незначимой регрессии.
Очевидно, что в этом случае, сумма квадратов «зеленых» расстояний, примерно соответствует сумме квадратов «красных». Это означает, что объясненная дисперсия примерно соответствует величине необъясненной дисперсии (MSR/MSE будет близко к 1).
Если ответ о значимости регрессии практически очевиден для 2-х вышеуказанных крайних ситуаций, то как сделать правильное заключение для промежуточных углов наклона линии регрессии?
Понятно, что если вычисленное на основании выборки значение MSR/MSE будет существенно больше некоторого критического значения, то регрессия значима, если нет, то не значима. Очевидно, что это значение должно быть больше 1, но как определить это критическое значение статистически обоснованным методом ?
Вспомним, что для формулирования статистического вывода (т.е. значима регрессия или нет) используют проверку гипотез . Для этого формулируют 2 гипотезы: нулевую Н 0 и альтернативную Н 1 . Для проверки значимости регрессии в качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. наклон прямой a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
Примечание : Даже если связи между переменными нет (a=0), то вычисленная на основании данных выборки оценка наклона - величина а , из-за случайности выборки будет близка, но все же отлична от 0.
По умолчанию принимается, что нулевая гипотеза верна – связи между переменными нет. Если это так, то:
- MSR/MSE будет близко к 1;
- Случайная величина F = MSR/MSE будет иметь F-распределение со степенями свободы 1 (в числителе) и n-2 (знаменателе). F является тестовой статистикой для проверки значимости регрессии.
Примечание : MSR и MSE являются случайными величинами (т.к. они получены на основе случайной выборки). Соответственно, выражение F=MSR/MSE, также является случайной величиной, которая имеет свое распределение, среднее значение и дисперсию .
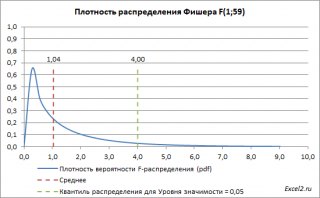
Ниже приведен график плотности вероятности F-распределения со степенями свободы 1 (в числителе) и 59 (знаменателе). 59=61-2, 61 наблюдение минус 2 степени свободы.
Если нулевая гипотеза верна, то значение F 0 =MSR/MSE, вычисленное на основании выборки, должно быть около ее среднего значения (т.е. около 1,04). Если F 0 будет существенно больше 1 (чем больше F0 отклоняется в сторону больших значений, тем это маловероятней), то это будет означать, что F не имеет F-распределение , а, следовательно, нулевую гипотезу нужно отклонить и принять альтернативную, утверждающую, что связь между переменными есть (значима).
Обычно предполагают, что если вероятность, того что F -статистика приняла значение F0 составляет менее 5%, то это событие маловероятно и нулевую гипотезу необходимо отклонить. 5% - это заданный исследователем уровень значимости , который может быть, например, 1% или 10%.
Значение статистики F0 может быть вычислено на основании выборки:
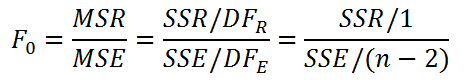
Вычисления в MS EXCEL
В MS EXCEL критическое значение для заданного уровня значимости F1-альфа, 1, n-2 можно вычислить по формуле = F.ОБР(1- альфа;1; n-2) или = F.ОБР.ПХ(альфа;1; n-2) . Другими словами требуется вычислить верхний альфа-квантиль F-распределения с соответствующими степенями свободы .
Таким образом, при значении статистики F0> F1-альфа, 1, n-2 мы имеем основание для отклонения нулевой гипотезы.
Значение F 0 можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции ЛИНЕЙН() :
= ИНДЕКС(ЛИНЕЙН($C$23:$C$83;$B$23:$B$83;;ИСТИНА);4;1)
В случае простой регрессии значение F0 также равно квадрату t-статистики, которую мы использовали при проверке двусторонней гипотезе о равенстве 0 коэффициента регрессии .
Проверку значимости регрессии можно также осуществить через вычисление p-значения. В этом случае вычисляют вероятность того, что случайная величина F примет значение F0 (это и есть p-значение), затем сравнивают p-значение с заданным уровнем значимости . Если p-значение больше уровня значимости, то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
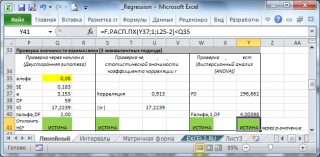
В MS EXCEL для проверки гипотезы используя p -значение используйте формулу = F.РАСП.ПХ(F0;1;n-2) < альфа
Если формула вернет ИСТИНА, то регрессия значима. Если формула вернет ЛОЖЬ, то у нас нет оснований отклонить нулевую гипотезу, т.е. «скорее всего» параметр модели a равен 0 (см. файл примера , где показано эквивалентность всех подходов проверки значимости регрессии).
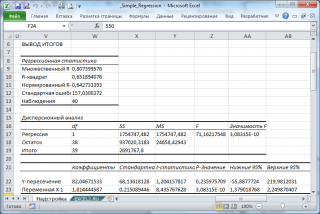
В программах статистики результаты процедуры F -теста выводят с помощью стандартной таблицы дисперсионного анализа . В файле примера такая таблица приведена на листе Таблица, которая построена на основе результатов, возвращаемых инструментом Регрессия надстройки Пакета анализа MS EXCEL .
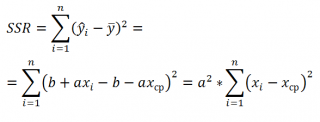

Комментарии