Диаграмма рассеяния в EXCEL

Построим диаграмму рассеяния для различных видов взаимосвязей двух переменных. Сгенерируем различные варианты трендов: линейный, квадратичный и затухающий синусоидальный.

Диаграмма рассеяния ( scatter plot ) используется для отображения возможной взаимосвязи между двумя переменными. Диаграмма рассеяния незаменима при проведении корреляционного и регрессионного анализа.

Возьмем 2 переменные Х и Y и, соответственно, выборку состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности зададим различные типы зависимости между переменными: линейную, квадратичную и затухающую синусоидальную. Для этого сгенерируем соответствующие тренды и настроим случайный разброс переменной Y (по нормальному закону ).

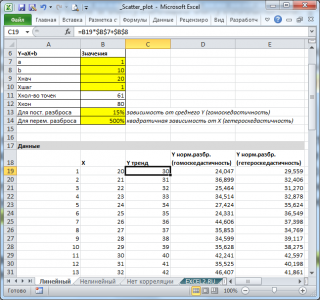
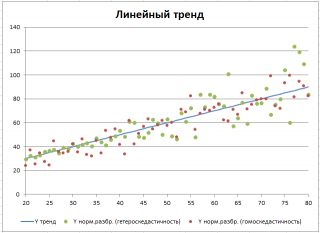
Сначала рассмотрим линейный тренд Y = aX + b (см. Файл примера, лист Линейный ). Параметры тренда (прямой линии) a и b зададим в отдельной табличке, там же зададим параметры отвечающие за величину дисперсии переменной Y.

Величину постоянного разброса (отвечающую за гомоскедастичность модели) будем задавать в % от среднего значения Y. Иногда, дисперсия переменной Y не постоянна (имеется неоднородность наблюдений - гетероскедастичность ). Поэтому, при построении формул учтем и такую возможность.

Для построения диаграммы рассеяния в файле примера использована диаграмма График , т.к. шаг по Х у нас задан постоянным. В случае реальных данных (переменная Х является случайной величиной, а не жестко заданной, как в нашем примере) используйте диаграмму типа Точечная. В файле примера реализовано оба варианта.

Примечание : Подробнее о построении диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .

Отображение информации о 3-х переменных на двухмерной диаграмме

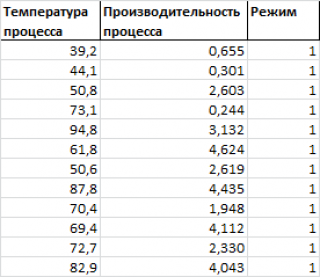
Предположим, что у нас имеются результаты измерения производительности некого непрерывного производственного процесса. Измерения проводились при различных рабочих температурах протекания процесса и в двух режимах.

Нам требуется построить двумерную диаграмму рассеяния (на плоскости), хотя у нас имеется 3 переменных: производительность, температура и режим .

Обратим внимание, что третья переменная Режим является категориальной (принимает только значения из ограниченного набора значений). В нашем случае переменная Режим принимает 2 значения: Режим №1 и Режим №2 (значения 1 и 2 присвоены номинально).

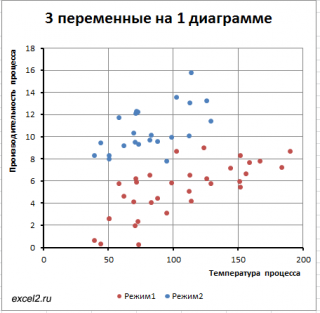
Пары значений ( производительность; температура ), относящиеся к Режиму №1 будем на диаграмме рассеяния выводить красным цветом, а относящиеся к Режиму №2 будем выводить синим ( файл примера лист 3-переменных ).

Такой же подход можно использовать для дискретных переменных , когда они принимают небольшое количество значений: 2-5.

Категоризованные диаграммы

Если третья переменная – непрерывная величина, то для отображения данных можно использовать так называемые категоризованные диаграммы (coplot = conditioning plot).

Теперь вместо категориальной переменной Режим у нас имеется непрерывная переменная Давление , которая принимает значения от 10 до 20. Предположим, что значение переменной Давление = 15, является неким пороговым и протекание процесса значительно отличается, если оно протекает при давлении от 10 до 15 и от 15 до 20. Используя этот факт строят 2 диаграммы:

• Пары значений ( производительность; температура ) при давлении от 10 до 15:
• Пары значений ( производительность; температура ) при давлении от 15 до 20.

Если пороговых значений 2, то понадобится 3 диаграммы и т.д. Эти диаграммы строятся аналогично диаграммам из предыдущего раздела.

Матрица диаграмм рассеивания

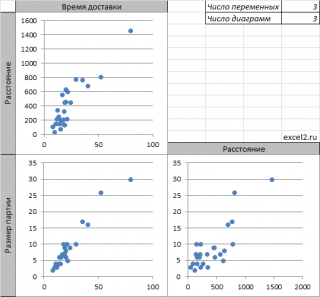
Для множественной регрессии, когда имеется 3 или более переменных, часто строят Матрицу диаграмм рассеивания (Matrix Scatter Plot, Scatter Plot Matrix - SPM).

Если имеется 3 переменных (x 1 , x 2 , y), то строятся 3 обычные диаграммы рассеяния отображающие парные взаимосвязи переменных: (x 1 , x 2 ); (x 1 , y); (x 2 , y).

Примечание : Чтобы найти количество диаграмм рассеяния в матрице, необходимо вычислить число сочетаний из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ЧИСЛКОМБ(4;2) =6.

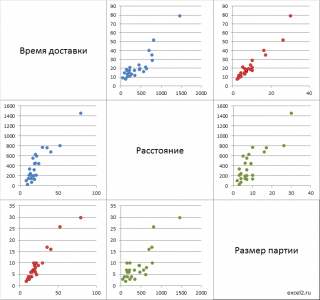
Иногда строят не только диаграмму (x 1 , x 2 ), но и (x 2 , x 1 ). В этом случае матрица будет содержать в 2 раза больше диаграмм рассеяния (см. файл примера лист Matrix ).

Примечание : Чтобы найти количество диаграмм рассеяния в такой (полной) матрице, необходимо вычислить число перестановок из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ПЕРЕСТ(4;2) =12.