Использование Пакета анализа EXCEL для построения множественной линейной регрессионной модели

Проведем множественный регрессионный анализ с помощью надстройки MS EXCEL Пакет анализа .

Эффективно использовать надстройку Пакет анализа могут только пользователи знакомые с теорией множественного регрессионного анализа .

В данной статье решены следующие задачи:

• Показано как в MS EXCEL выполнить регрессионный анализ с помощью надстройки Пакет анализа (инструмент Регрессия), т.е. как вызвать надстройку и правильно заполнить входные данные;
• Даны пояснения по разделам отчета, формированного надстройкой;
• Даны комментарии обо всех показателях, рассчитанных надстройкой, и приведены ссылки на соответствующие разделы статей, посвященные простой линейной регрессии .

В надстройке Пакет анализа для построения линейной регрессионной модели (как простой , так и множественной ) имеется специальный инструмент Регрессия .

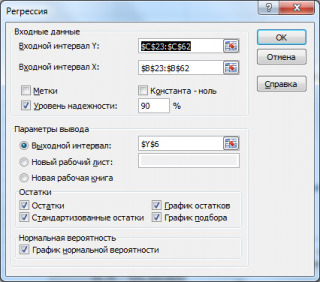
После выбора этого инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Надстройка ):

• Входной интервал Y : ссылка на массив значений переменной Y. Ссылку можно указать с заголовком. В этом случае, при выводе результатов надстройка использует Ваш заголовок (для этого в окне требуется установить галочку Метки );
• Входной интервал Х : ссылка на значения переменных Х (нужно указать все столбцы со значениями Х). Ссылку рекомендуется делать на диапазон с заголовками (в окне не забудьте установить галочку Метки );
• Константа-ноль : если галочка установлена, то надстройка подбирает плоскость регрессии с b 0 =0;
• Уровень надежности : Это значение используется для построения доверительных интервалов для наклона и сдвига . Уровень надежности = 1- альфа . Если галочка не установлена или установлена, но уровень значимости = 95%, то надстройка все равно рассчитывает границы доверительных интервалов, причем дублирует их. Если галочка установлена, а уровень надежности отличен от 95%, то рассчитываются 2 доверительных интервала : один для 95%, другой для введенного значения. Для демонстрации вышесказанного введем 90%;
• Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона;
• Остатки : будут вычислены остатки модели , т.е. разница между наблюденными и предсказанными значениями Yi для всех наблюдений n;
• Стандартизированные остатки : Вышеуказанные значения остатков будут поделены на значение их стандартного отклонения ;
• График остатков : Для каждой переменной X _j будет построена точечная диаграмма : значения остатков и соответствующее значение Х _ji (при прогнозировании на основании значений 2-х переменных Х будет построено 2 диаграммы (j=1 и 2));
• График подбора: Для каждой переменной X _j будут построены точечные диаграммы с двумя рядами данных : точки данных (X _ji ;Y _i ) и (X _ji ;Y _{iпредсказанное} );
• График нормальной вероятности: Будет построена точечная диаграмма с названием График нормального распределения . По сути - это график значений переменной Y, отсортированных по возрастанию .

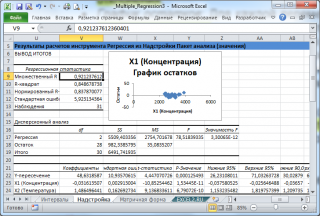
В результате вычислений будет заполнен указанный Выходной интервал.

Тот же результат можно получить с помощью формул (см. файл примера лист Надстройка , столбцы I:T).

Результаты вычислений, выполненных надстройкой, полностью совпадают с вычислениями сделанными нами в статье про множественную линейную регрессию с помощью функций ЛИНЕЙН() , ТЕНДЕНЦИЯ() и др. Использование альтернативных формул помогает разобраться с алгоритмом расчета показателей регрессии.

Отчет, сформированный надстройкой, состоит из следующих разделов:

Раздел «Регрессионная статистика»:

• Множественный R. В случае множественной линейной регрессии - это квадратный корень из коэффициента детерминации R ²
• R-квадрат . В случае множественной линейной регрессии – это коэффициент детерминации R ²
• Нормированный R-квадрат . Подробнее см. здесь (англ. термин Adjusted R-squared)
• Стандартная ошибка . Подробнее см. здесь ;
• Наблюдения . Количество значений Y.

Раздел «Дисперсионный анализ»:

См. раздел Проверка гипотез в статье о множественной регрессии .

• df – степени свободы (Degrees of Freedom).
• SS – сумма квадратов (Sum of Squares)
• MS – SS/df (MSR и MSE)
• F – значение статистики F ₀ (MSR/MSE)
• Значимость F – p-значение, функция F.РАСП.ПХ()

Другие результаты:

• Коэффициенты : оценка параметров модели b _j . См. раздел Оценка неизвестных параметров .
• Стандартная ошибка : Стандартные ошибки вышеуказанных статистик
• t-статистика : значение тестовой статистики t ₀ , которая имеет распределение Стьюдента . Используется для проверки значимости индивидуальных коэффициентов. t ₀ – отношение оценки коэффициента регрессии и его стандартного отклонения (модуль этого значения). Если это значение меньше критического значения =СТЬЮДЕНТ.ОБР.2Х(0,05;DF) , то коэффициент не значимый.
• P-Значение : Используется для проверки значимости индивидуальных коэффициентов. Если вероятность t-статистики меньше уровня значимости (обычно 0,05), то коэффициент не значимый
• Нижние 95% и Верхние 95%: границы доверительных интервалов для оценок неизвестных параметров модели с уровнем значимости =1-95%=5%=0,05.