МНК: Метод Наименьших Квадратов в EXCEL
11 ноября 2018 г.
- Группы статей
- Статистический анализ
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью линейной функции y = a x + b .
Метод наименьших квадратов (англ. Ordinary Least Squares , OLS ) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным.
Рассмотрим приближение функциями, зависящими только от одной переменной:
- Линейная: y=ax+b (эта статья)
- Логарифмическая : y=a*Ln(x)+b
- Степенная : y=a*x m
- Экспоненциальная : y=a*EXP(b*x)+с
- Квадратичная : y=ax 2 +bx+c
Примечание : Случаи приближения полиномом с 3-й до 6-й степени рассмотрены в этой статье. Приближение тригонометрическим полиномом рассмотрено здесь.
Линейная зависимость
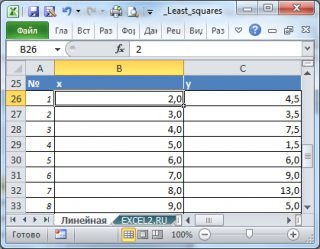
Нас интересует связь 2-х переменных х и y . Имеется предположение, что y зависит от х по линейному закону y = ax + b . Чтобы определить параметры этой взаимосвязи исследователь провел наблюдения: для каждого значения х i произведено измерение y i (см. файл примера ). Соответственно, пусть имеется 20 пар значений (х i ; y i ).
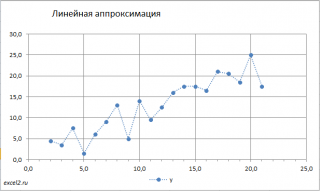
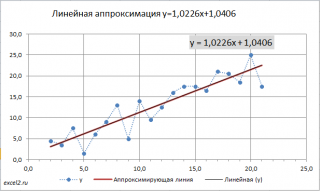
Для наглядности рекомендуется построить диаграмму рассеяния.
Примечание: Если шаг изменения по х постоянен, то для построения диаграммы рассеяния можно использовать тип График , если нет, то необходимо использовать тип диаграммы Точечная .
Из диаграммы очевидно, что связь между переменными близка к линейной. Чтобы понять какая из множества прямых линий наиболее «правильно» описывает зависимость между переменными, необходимо определить критерий, по которому будут сравниваться линии.
В качестве такого критерия используем выражение:
где ŷ i = a * x i + b ; n – число пар значений (в нашем случае n=20)
Вышеуказанное выражение представляет собой сумму квадратов расстояний между наблюденными значениями y i и ŷ i и часто обозначается как SSE ( Sum of Squared Errors ( Residuals ), сумма квадратов ошибок (остатков) ) .
Метод наименьших квадратов заключается в подборе такой линии ŷ = ax + b , для которой вышеуказанное выражение принимает минимальное значение.
Примечание: Любая линия в двухмерном пространстве однозначно определяется значениями 2-х параметров: a (наклон) и b (сдвиг).
Считается, что чем меньше сумма квадратов расстояний, тем соответствующая линия лучше аппроксимирует имеющиеся данные и может быть в дальнейшем использована для прогнозирования значений y от переменной х. Понятно, что даже если в действительности никакой взаимосвязи между переменными нет или связь нелинейная, то МНК все равно подберет «наилучшую» линию. Таким образом, МНК ничего не говорит о наличии реальной взаимосвязи переменных, метод просто позволяет подобрать такие параметры функции a и b , для которых вышеуказанное выражение минимально.
Проделав не очень сложные математические операции (подробнее см. статью про квадратичную зависимость ), можно вычислить параметры a и b :
Как видно из формулы, параметр a представляет собой отношение ковариации и дисперсии , поэтому в MS EXCEL для вычисления параметра а можно использовать следующие формулы (см. файл примера лист Линейная ):
= КОВАР(B26:B45;C26:C45)/ ДИСП.Г(B26:B45) или
= КОВАРИАЦИЯ.В(B26:B45;C26:C45)/ДИСП.В(B26:B45)
Также для вычисления параметра а можно использовать формулу = НАКЛОН(C26:C45;B26:B45) . Для параметра b используйте формулу = ОТРЕЗОК(C26:C45;B26:B45) .
И наконец, функция ЛИНЕЙН() позволяет вычислить сразу оба параметра. Для ввода формулы ЛИНЕЙН(C26:C45;B26:B45) необходимо выделить в строке 2 ячейки и нажать CTRL + SHIFT + ENTER (см. статью про формулы массива, возвращающими несколько значений ). В левой ячейке будет возвращено значение а , в правой – b .
Примечание : Чтобы не связываться с вводом формул массива потребуется дополнительно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);1) или просто = ЛИНЕЙН(C26:C45;B26:B45) вернет параметр, отвечающий за наклон линии, т.е. а . Формула = ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);2) вернет параметр, отвечающий за пересечение линии с осью Y, т.е. b .
Вычислив параметры, на диаграмме рассеяния можно построить соответствующую линию.
Инструмент диаграммы Линия тренда
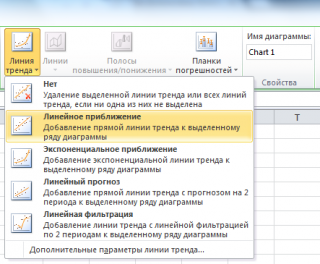
Еще одним способом построения прямой линии по методу наименьших квадратов является инструмент диаграммы Линия тренда . Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение .
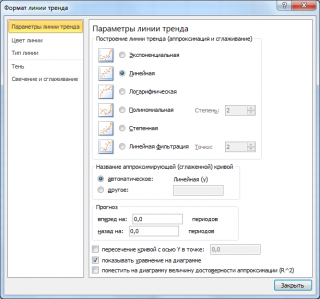
Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме.
Примечание : Для того, чтобы параметры совпадали необходимо, чтобы тип у диаграммы был Точечная, а не График . Дело в том, что при построении диаграммы График значения по оси Х не могут быть заданы пользователем (пользователь может указать только подписи, которые не влияют на расположение точек). Вместо значений Х используется последовательность 1; 2; 3; … (для нумерации категорий). Поэтому, если строить линию тренда на диаграмме типа График , то вместо фактических значений Х будут использованы значения этой последовательности, что приведет к неверному результату (если, конечно, фактические значения Х не совпадают с последовательностью 1; 2; 3; …).
СОВЕТ : Подробнее о построении диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
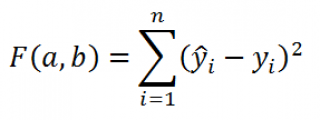
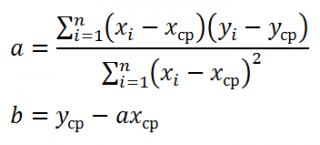
Комментарии