Проверка простых гипотез критерием хи-квадрат Пирсона в EXCEL
13 декабря 2016 г.
- Группы статей
- Статистический вывод
Рассмотрим применение в MS EXCEL критерия хи-квадрат Пирсона для проверки простых гипотез.
После получения экспериментальных данных (т.е. когда имеется некая выборка ) обычно производится выбор закона распределения, наиболее хорошо описывающего случайную величину, представленную данной выборкой . Проверка того, насколько хорошо экспериментальные данные описываются выбранным теоретическим законом распределения, осуществляется с использованием критериев согласия . Нулевой гипотезой , обычно выступает гипотеза о равенстве распределения случайной величины некоторому теоретическому закону.
Сначала рассмотрим применение критерия согласия Пирсона Х 2 (хи-квадрат) в отношении простых гипотез (параметры теоретического распределения считаются известными). Затем - применение критерияв случае сложных гипотез , когда задается только форма распределения, а параметры этого распределения и значение статистики Х 2 оцениваются/рассчитываются на основании одной и той же выборки .
Примечание : Применение критерия согласия Пирсона Х 2 в отношении сложных гипотез см. статью Проверка сложных гипотез критерием хи-квадрат Пирсона в MS EXCEL .
Примечание : В англоязычной литературе процедура применения критерия согласия Пирсона Х 2 имеет название The chi-square goodness of fit test .
Напомним процедуру проверки гипотез:
- на основе выборки вычисляется значение статистики , которая соответствует типу проверяемой гипотезы. Например, для проверки гипотезы о равенстве среднего μ некоторому заданному значению μ 0 используется t -статистика (если стандартное отклонение не известно);
- при условии истинности нулевой гипотезы , распределение этой статистики известно и может быть использовано для вычисления вероятностей (например, для t -статистики это распределение Стьюдента );
- вычисленное на основе выборки значение статистики сравнивается с критическим для заданного уровня значимости значением ( α-квантилем );
- нулевую гипотезу отвергают, если значение статистики больше критического (или если вероятность получить это значение статистики ( p-значение ) меньше уровня значимости , что является эквивалентным подходом).
Проведем проверку гипотез для различных распределений.
Дискретный случай
Предположим, что два человека играют в кости. У каждого игрока свой набор костей. Игроки по очереди кидают сразу по 3 кубика. Каждый раунд выигрывает тот, кто выкинет за раз больше шестерок. Результаты записываются. У одного из игроков после 100 раундов возникло подозрение, что кости его соперника – несимметричные, т.к. тот часто выигрывает (часто выбрасывает шестерки). Он решил проанализировать насколько вероятно такое количество исходов противника.
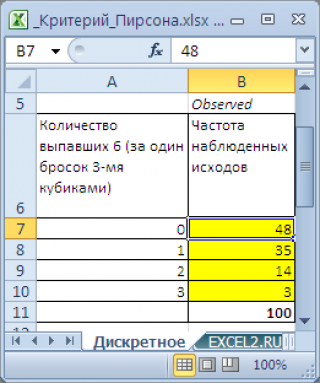
Примечание : Т.к. кубиков 3, то за раз можно выкинуть 0; 1; 2 или 3 шестерки, т.е. случайная величина может принимать 4 значения.
Из теории вероятности нам известно, что если кубики симметричные, то вероятность выпадения шестерок подчиняется биномиальному закону . Поэтому, после 100 раундов частоты выпадения шестерок могут быть вычислены с помощью формулы =БИНОМ.РАСП(A7;3;1/6;ЛОЖЬ)*100
В формуле предполагается, что в ячейке А7 содержится соответствующее количество выпавших шестерок в одном раунде.
Примечание : Расчеты приведены в файле примера на листе Дискретное .
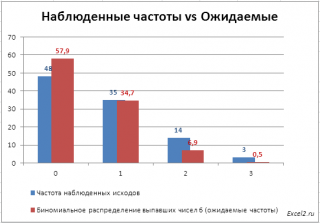
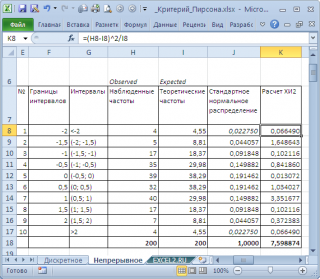
Для сравнения наблюденных (Observed) и теоретических частот (Expected) удобно пользоваться гистограммой .
При значительном отклонении наблюденных частот от теоретического распределения, нулевая гипотеза о распределении случайной величины по теоретическому закону, должна быть отклонена. Т.е., если игральные кости соперника несимметричны, то наблюденные частоты будут «существенно отличаться» от биномиального распределения .
В нашем случае на первый взгляд частоты достаточно близки и без вычислений сложно сделать однозначный вывод. Применим критерий согласия Пирсона Х 2 , чтобы вместо субъективного высказывания «существенно отличаться», которое можно сделать на основании сравнения гистограмм , использовать математически корректное утверждение.
Используем тот факт, что в силу закона больших чисел наблюденная частота (Observed) с ростом объема выборки n стремится к вероятности, соответствующей теоретическому закону (в нашем случае, биномиальному закону ). В нашем случае объем выборки n равен 100.
Введем тестовую статистику , которую обозначим Х 2 :
где O l – это наблюденная частота событий, что случайная величина приняла определенные допустимые значения, E l – это соответствующая теоретическая частота (Expected). L – это количество значений, которые может принимать случайная величина (в нашем случае равна 4).
Примечание : Вышеуказанная статистика является частным случаем статистики используемой для вычисления критерия независимости хи-квадрат (см. статью Критерий независимости хи-квадрат в MS EXCEL ).
Как видно из формулы, эта статистика является мерой близости наблюденных частот к теоретическим, т.е. с помощью нее можно оценить «расстояния» между этими частотами. Если сумма этих «расстояний» «слишком велика», то эти частоты «существенно отличаются». Понятно, что если наш кубик симметричный (т.е. применим биномиальный закон ), то вероятность того, что сумма «расстояний» будет «слишком велика» будет малой. Чтобы вычислить эту вероятность нам необходимо знать распределение статистики Х 2 ( статистика Х 2 вычислена на основе случайной выборки , поэтому она является случайной величиной и, следовательно, имеет свое распределение вероятностей ).
Из многомерного аналога интегральной теоремы Муавра-Лапласа известно, что при n—>∞ наша случайная величина Х 2 асимптотически распределена по закону Х 2 с L - 1 степенями свободы.
Итак, если вычисленное значение статистики Х 2 (сумма «расстояний» между частотами) будет больше чем некое предельное значение, то у нас будет основание отвергнуть нулевую гипотезу . Как и при проверке параметрических гипотез , предельное значение задается через уровень значимости . Если вероятность того, что статистика Х 2 примет значение меньше или равное вычисленному ( p -значение ), будет меньше уровня значимости , то нулевую гипотезу можно отвергнуть.
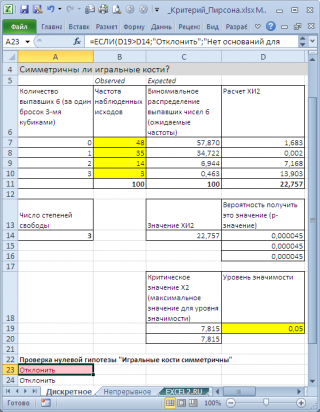
В нашем случае, значение статистики равно 22,757. Вероятность, что статистика Х 2 примет значение больше или равное 22,757 очень мала (0,000045) и может быть вычислена по формулам =ХИ2.РАСП.ПХ(22,757;4-1) или =ХИ2.ТЕСТ(Observed; Expected)
Примечание : Функция ХИ2.ТЕСТ() специально создана для проверки связи между двумя категориальными переменными (см. статью про критерий независимости ).
Вероятность 0,000045 существенно меньше обычного уровня значимости 0,05. Так что, у игрока есть все основания подозревать своего противника в нечестности ( нулевая гипотеза о его честности отвергается).
При применении критерия Х 2 необходимо следить за тем, чтобы объем выборки n был достаточно большой, иначе будет неправомочна аппроксимация Х 2 -распределением распределения статистики Х 2 . Обычно считается, что для этого достаточно, чтобы наблюденные частоты (Observed) были больше 5. Если это не так, то малые частоты объединяются в одно или присоединяются к другим частотам, причем объединенному значению приписывается суммарная вероятность и, соответственно, уменьшается число степеней свободы Х 2 -распределения .
Для того чтобы улучшить качество применения критерия Х 2 ( увеличить его мощность ), необходимо уменьшать интервалы разбиения (увеличивать L и, соответственно, увеличивать количество степеней свободы ), однако этому препятствует ограничение на количество попавших в каждый интервал наблюдений (д.б.>5).
Примечание : Рассмотренный выше пример является частным случаем применения критерия независимости хи-квадрат (chi-square test), который позволяет определить есть ли связь между двумя категориальными переменными (см. статью Критерий независимости хи-квадрат в MS EXCEL ).
СОВЕТ : О проверке других видов гипотез см. статью Проверка статистических гипотез в MS EXCEL .
Непрерывный случай
Критерий согласия Пирсона Х 2 можно применить так же в случае непрерывного распределения .
Рассмотрим некую выборку , состоящую из 200 значений. Нулевая гипотеза утверждает, что выборка сделана из стандартного нормального распределения .
Примечание : Cлучайные величины в файле примера на листе Непрерывное сгенерированы с помощью формулы =НОРМ.СТ.ОБР(СЛЧИС()) . Поэтому, новые значения выборки генерируются при каждом пересчете листа.
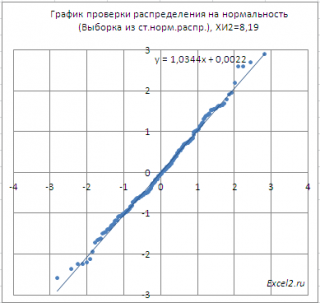
Соответствует ли имеющийся набор данных нормальному распределению можно визуально оценить с помощью графика проверки на нормальность (normal probability plot) .
Как видно из диаграммы, значения выборки довольно хорошо укладываются вдоль прямой. Однако, как и в дискретном случае для проверки гипотезы применим Критерий согласия Пирсона Х 2 .
Для этого разобьем диапазон изменения случайной величины на интервалы с шагом 0,5 стандартных отклонений . Вычислим наблюденные и теоретические частоты. Наблюденные частоты вычислим с помощью функции ЧАСТОТА() , а теоретические – с помощью функции НОРМ.СТ.РАСП() .
Примечание : Как и для дискретного случая , необходимо следить, чтобы выборка была достаточно большая, а в интервал попадало >5 значений.
Вычислим статистику Х 2 и сравним ее с критическим значением для заданного уровня значимости (0,05). Т.к. мы разбили диапазон изменения случайной величины на 10 интервалов, то число степеней свободы равно 9. Критическое значение можно вычислить по формуле =ХИ2.ОБР.ПХ(0,05;9) или =ХИ2.ОБР(1-0,05;9)
На диаграмме выше видно, что значение статистики равно 8,19, что существенно выше критического значения – нулевая гипотеза не отвергается.
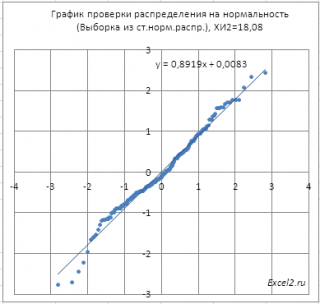
Ниже приведена диаграмма , на которой выборка приняла маловероятное значение и на основании критерия согласия Пирсона Х 2 нулевая гипотеза была отклонена (не смотря на то, что случайные значения были сгенерированы с помощью формулы =НОРМ.СТ.ОБР(СЛЧИС()) , обеспечивающей выборку из стандартного нормального распределения ).
Нулевая гипотеза отклонена, хотя визуально данные располагаются довольно близко к прямой линии.
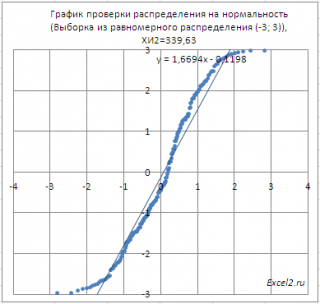
В качестве примера также возьмем выборку из непрерывного равномерного распределения U(-3; 3). В этом случае, даже из графика очевидно, что нулевая гипотеза должна быть отклонена.
Критерий согласия Пирсона Х 2 также подтверждает, что нулевая гипотеза должна быть отклонена.
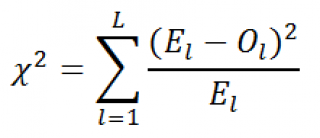
Комментарии