Биномиальное распределение. Дискретные распределения в EXCEL
29 октября 2016 г.
- Группы статей
- Распределения вероятностей
Рассмотрим Биномиальное распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL БИНОМ.РАСП() построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения p, математического ожидания распределения и стандартного отклонения. Также рассмотрим распределение Бернулли.
Определение . Пусть проводятся n испытаний, в каждом из которых может произойти только 2 события: событие «успех» с вероятностью p или событие «неудача» с вероятностью q =1-p (так называемая Схема Бернулли, Bernoulli trials ).
Вероятность получения ровно x успехов в этих n испытаниях равна:

Примечание : Порядок получения успехов значения не имеет. Если важен порядок, то см. статью Отрицательное Биномиальное распределение .
Количество успехов в выборке x является случайной величиной, которая имеет Биномиальное распределение (англ. Binomial distribution ) p и n – являются параметрами этого распределения.
Примечание
: Запись
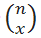 означает количество
сочетаний
из
n
элементов по
x
. Для сочетаний также используется запись
означает количество
сочетаний
из
n
элементов по
x
. Для сочетаний также используется запись
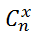 . Подробнее о сочетаниях см. статью
Сочетания без повторений: Комбинаторика в MS EXCEL
.
. Подробнее о сочетаниях см. статью
Сочетания без повторений: Комбинаторика в MS EXCEL
.
Напомним, что для применения схемы Бернулли и соответственно Биномиального распределения, должны быть выполнены следующие условия:
- каждое испытание должно иметь ровно два исхода, условно называемых «успехом» и «неудачей».
- результат каждого испытания не должен зависеть от результатов предыдущих испытаний (независимость испытаний).
- вероятность успеха p должна быть постоянной для всех испытаний.
Биномиальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Биномиального распределения имеется функция БИНОМ.РАСП() , английское название - BINOM.DIST(), которая позволяет вычислить вероятность того, что в выборке будет ровно х «успехов» (т.е. функцию плотности вероятности p(x), см. формулу выше), и интегральную функцию распределения (вероятность того, что в выборке будет x или меньше «успехов», включая 0).
СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
До MS EXCEL 2010 в EXCEL была функция БИНОМРАСП() , которая также позволяет вычислить функцию распределения и плотность вероятности p(x). БИНОМРАСП() оставлена в MS EXCEL 2010 для совместимости.
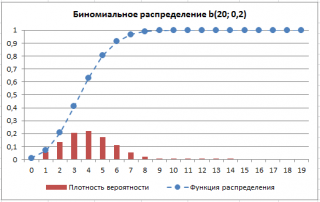
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Биномиальное распределения имеет обозначение B ( n ; p ) .
Примечание : Для построения интегральной функции распределения идеально подходит диаграмма типа График , для плотности распределения – Гистограмма с группировкой . Подробнее о построении диаграмм читайте статью Основные типы диаграмм.
Примечание : Для удобства написания формул в файле примера созданы Имена для параметров Биномиального распределения : n и p.
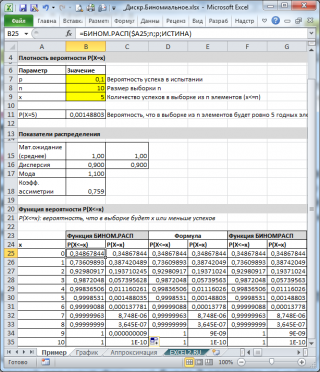
В файле примера приведены различные расчеты вероятности с помощью функций MS EXCEL:
Как видно на картинке выше, предполагается, что:
- В бесконечной совокупности, из которой делается выборка, содержится 10% (или 0,1) годных элементов (параметр p , третий аргумент функции = БИНОМ.РАСП() )
- Чтобы вычислить вероятность, того что в выборке из 10 элементов (параметр n , второй аргумент функции) будет ровно 5 годных элементов (первый аргумент), нужно записать формулу: =БИНОМ.РАСП(5; 10; 0,1; ЛОЖЬ)
- Последний, четвертый элемент, установлен =ЛОЖЬ, т.е. возвращается значение функции плотности распределения .
Если значение четвертого аргумента =ИСТИНА, то функция БИНОМ.РАСП() возвращает значение интегральной функции распределения или просто Функцию распределения . В этом случае можно рассчитать вероятность того, что в выборке количество годных элементов будет из определенного диапазона, например, 2 или меньше (включая 0).
Для этого нужно записать формулу: = БИНОМ.РАСП(2; 10; 0,1; ИСТИНА)
Примечание : При нецелом значении х, дробная часть отбрасывается . Например, следующие формулы вернут одно и тоже значение: =БИНОМ.РАСП( 2 ; 10; 0,1; ИСТИНА) =БИНОМ.РАСП( 2,9 ; 10; 0,1; ИСТИНА)
Примечание : В файле примера плотность вероятности и функция распределения также вычислены с использованием определения и функции ЧИСЛКОМБ() .
Показатели распределения
В файле примера на листе Пример имеются формулы для расчета некоторых показателей распределения:
- математического ожидания =n*p;
- дисперсии (квадрата стандартного отклонения) = n*p*(1-p);
- моды = (n+1)*p;
- коэффициента асимметрии =(1-2*p)*КОРЕНЬ(n*p*(1-p)).
Выведем формулу математического ожидания Биномиального распределения , используя Схему Бернулли .
По определению случайная величина Х в схеме Бернулли (Bernoulli random variable) имеет функцию распределения :
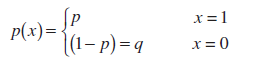
Это распределение называется распределение Бернулли .
Примечание : распределение Бернулли – частный случай Биномиального распределения с параметром n=1.
Найдем математическое ожидание ( среднее, mean ) распределения Бернулли ( x принимает только 2 значения).
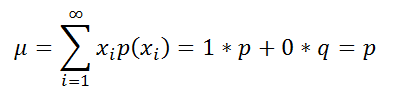
Предположим, что мы провели n последовательных испытаний Бернулли и у нас сформировалась выборка , состоящая из n элементов: x1, x2, …, xn (каждое из которых равно 0 или 1). Сумма этих случайных величин Y=X1+X2+…+Xn, в свою очередь, также является случайной величиной и, как мы помним, будет иметь Биномиальное распределение с параметрами n и p .
Учитывая, что математическое ожидание для каждого x i равно p , то для соответствующего Биномиального распределения μ=p*n.
Аналогичным образом, можно вычислить дисперсию Биномиального распределения.
Для этого сначала найдем дисперсию ( второй момент, variance ) распределения Бернулли :
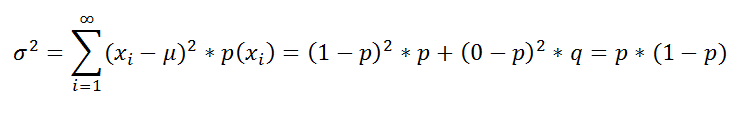
Соответственно, дисперсия для Биномиального распределения равна σ 2 =n*p*(1-p)= n*p*q.
Генерация случайных чисел. Распределение Бернулли
С помощью надстройки Пакет анализа можно сгенерировать случайные числа , извлеченные из распределения Бернулли .
СОВЕТ : О надстройке Пакет анализа можно прочитать в статье Надстройка Пакет анализа MS EXCEL .
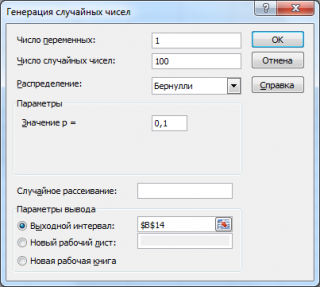
Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5 и 0,9. Для этого в окне Генерация случайных чисел установим следующие параметры для каждой вероятности p:
Примечание : Если установить опцию Случайное рассеивание ( Random Seed ), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию =25 можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции Случайное рассеивание может запутать. Лучше было бы ее перевести как Номер набора со случайными числами .
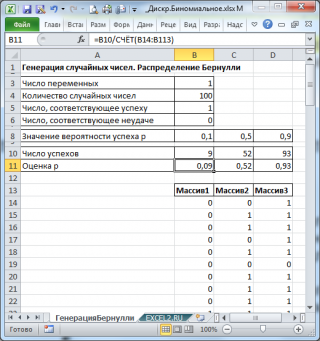
В итоге будем иметь 3 столбца по 100 чисел, на основании которых можно, например, оценить вероятность успеха p по формуле: Число успехов/100 (см. файл примера лист ГенерацияБернулли ).
Примечание : Для распределения Бернулли с p=0,5 можно использовать формулу =СЛУЧМЕЖДУ(0;1) , которая соответствует дискретному равномерному распределению .
Генерация случайных чисел. Биномиальное распределение
С помощью надстройки Пакет анализа можно сгенерировать случайные числа , извлеченные из Биномиального распределения .
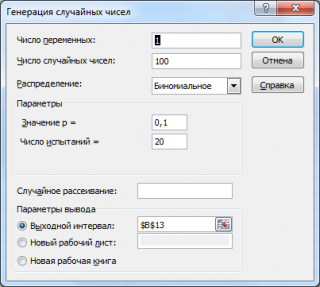
Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5; 0,9. Количество испытаний n установим 20. Для этого в окне Генерация случайных чисел установим следующие параметры для каждой вероятности p:
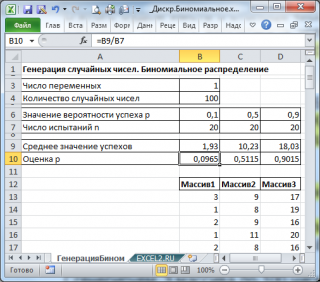
В итоге будем иметь 3 столбца чисел, на основании которых можно, например, оценить вероятность успеха p по формуле: Среднее значение успехов/ n (см. файл примера лист ГенерацияБином ).
Примечание : Для генерирования массива чисел, распределенных по Биномиальному закону , можно использовать формулу =БИНОМ.ОБР(20; p; СЛЧИС()) , где p – вероятность успеха. Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист ГенерацияБином ).
Оценка параметра p
В схеме Бернулли оценить параметр распределения p можно по формуле =СУММ(B14:B113)/СЧЁТ(B14:B113) . В формуле предполагается, что массив случайных чисел находится в диапазоне B14:B113 .
Оценить параметр Биномиального распределения p можно по формуле = СРЗНАЧ(B13:B112)/n (предполагается, что случайные числа сгенерированы формулой =БИНОМ.ОБР(n; p; СЛЧИС() ). Также в формуле предполагается, что массив случайных чисел находится в диапазоне B13:B112 .
Обратная функция БИНОМ.ОБР()
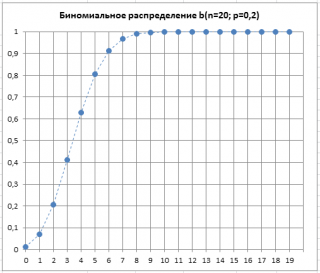
Вспомним график функции Биномиального распределения :
Решим задачу. Предположим, что для целей контроля качества нам требуется определить наибольшее допустимое количество дефектных изделий, которое еще позволяет обойтись без отбраковки всей партии.
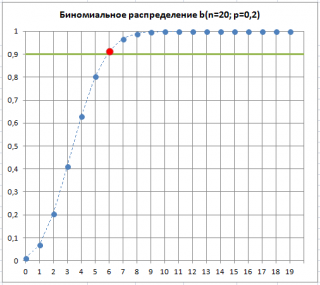
Задана величина выборки из партии ( n =20) и р= 0,2 - доля дефектных изделий, которая обычно наблюдается в данном производственном процессе. Также пусть задана вероятность допустить ошибку 1-го рода (см. статью про уровень доверия ) равная 90%. Пороговый приемочный критерий можно вычислить по формуле =БИНОМ.ОБР(20; 0,2; 90%) . Формула вернет значение 6 - наибольшее количество дефектных изделий, допустимое в выборке .
Примечание : Третий аргумент функции БИНОМ.ОБР() называется Альфа ( α error, type I error, риск производителя, альфа-риск ) и представляет собой вероятность допустить ошибку 1-го рода при проверке статистической гипотезы (см. статью Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна) ).
Предположим, что в выборке обнаружилось 7 дефектных изделий. Это означает, что «очень вероятна» ситуация, что изменилась доля дефектных изделий p , которая является характеристикой нашего производственного процесса. Хотя такая ситуация «очень вероятна», но существует вероятность (альфа-риск, ошибка 1-го рода, «ложная тревога»), что все же p осталась без изменений, а увеличенное количество дефектных изделий обусловлено случайностью выборки.
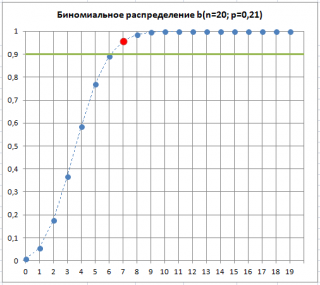
Как видно на рисунке ниже, 7 – количество дефектных изделий, которое допустимо для процесса с p=0,21 при том же значении Альфа . Это служит иллюстрацией, что при превышении порогового значения дефектных изделий в выборке, p «скорее всего» увеличилось. Фраза «скорее всего» означает, что существует всего лишь 10% вероятность (100%-90%) того, что отклонение доли дефектных изделий выше порогового вызвано только сучайными причинами.
Таким образом, превышение порогового количества дефектных изделий в выборке, может служить сигналом, что процесс расстроился и стал выпускать б о льший процент бракованных изделий.
Примечание : До MS EXCEL 2010 в EXCEL была функция КРИТБИНОМ() , которая эквивалентна БИНОМ.ОБР() . КРИТБИНОМ() оставлена в MS EXCEL 2010 и выше для совместимости.
Связь Биномиального распределения с другими распределениями
Если параметр n Биномиального распределения стремится к бесконечности, а p стремится к 0, то в этом случае Биномиальное распределение может быть аппроксимировано Распределением Пуассона . Можно сформулировать условия, когда приближение распределением Пуассона работает хорошо:
- p <0,1 (чем меньше p и больше n , тем приближение точнее);
- p >0,9 (учитывая, что q =1- p , вычисления в этом случае необходимо производить через q (а х нужно заменить на n - x ). Следовательно, чем меньше q и больше n , тем приближение точнее).
При 0,1<=p<=0,9 и n*p>10 Биномиальное распределение можно аппроксимировать Нормальным распределением .
В свою очередь, Биномиальное распределение может служить хорошим приближением Гипергеометрического распределения , когда размер совокупности N Гипергеометрического распределения гораздо больше размера выборки n (т.е., N>>n или n/N<<1).
Подробнее о связи вышеуказанных распределений, можно прочитать в статье Взаимосвязь некоторых распределений друг с другом в MS EXCEL . Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Комментарии