Ошибка второго рода и кривые оперативной характеристики в EXCEL
24 ноября 2016 г.
- Группы статей
- Статистический вывод
Определим выражение для вычисления ошибки второго рода и мощности теста, построим в MS EXCEL кривые оперативной характеристики (Operating-characteristic curves).
Тема этой статьи – вычисление ошибки второго рода (type II error) при проверке гипотез . Основная статья про проверку гипотез находится здесь .
Напомним, что процедура проверки гипотез состоит из следующих шагов:
- из исследуемого распределения берется выборка ;
- на основании значений выборки вычисляется тестовая статистика ;
- значение тестовой статистики сравнивается со значениями, соответствующим заданному уровню значимости (ошибке первого рода) ;
- по результату сравнения делается вывод об отклонении (или не отклонении) нулевой гипотезы .
Обычно с проверкой гипотез связывают 2 типа ошибок. Если нулевая гипотеза отклоняется, когда она верна – это ошибка первого рода (обозначается α, альфа ). Если нулевая гипотеза не отклоняется, когда она неверна, то это ошибка второго рода (обозначается β, бета ).
Ошибка первого рода часто называется риском производителя. Это осознанный риск, на который идет производитель продукции, т.к. он определяет вероятность того, что годная продукция может быть забракована, хотя на самом деле она таковой не является. Величина ошибки первого рода задается перед проверкой гипотезы , таким образом, она контролируется исследователем напрямую и может быть задана в соответствии с условиями решаемой задачи. После этого, процедура проверки гипотезы составляется таким образом, чтобы вероятность ошибки второго рода была как можно меньше.
Ошибка второго рода β зависит от размера выборки n и уровня значимости α , и поэтому контролируется косвенно. Чем больше размер выборки , тем меньше ошибка второго рода (при прочих равных).
Часто также используют величину 1-β , которая называется мощностью статистического критерия (мощностью теста, мощностью исследования, англ. power of a statistical test). Мощность статистического критерия - это вероятность правильно отклонить нулевую гипотезу. Чем ближе эта величина к единице, тем меньше у нас шансов ошибиться при проверке гипотезы (тем лучше критерий различает гипотезы Н 0 и Н 1 ).
Ошибку второго рода вычисляют для каждого вида проверки гипотез по-разному. Получим выражение для вычисления ошибки второго рода для проверки двусторонней гипотезы о равенстве среднего значения распределения некоторой величине (стандартное отклонение известно) .
Для проверки гипотезы этого типа используется тестовая статистика Z 0 : 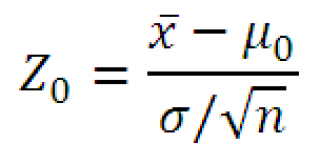
которая имеет стандартное нормальное распределение .
Чтобы найти Ошибку второго рода необходимо предположить, что гипотеза Н 0 : μ=μ 0 не верна, и соответственно истинное среднее значение распределения μ=μ 0 +Δ, где Δ>0. В этом случае, тестовая статистика Z 0 будет иметь нормальное распределение N(Δ√n/σ;1), т.е. будет смещено вправо на Δ√n/σ (см. файл примера на листе Бета ). 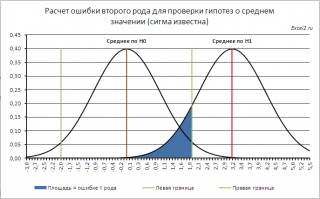
Согласно определения, ошибка второго рода равна вероятности, принять нулевую гипотезу, если на самом деле справедлива Н 1 . Эта вероятность соответствует выделенной на рисунке области. Статистика Z 0 , в этом случае, примет значение между -Z α/2 и Z α/2 (эти значения соответствуют границам доверительного интервала ). Z α/2 – это верхний α/2-квантиль стандартного нормального распределения .
Определим ошибку второго рода в терминах стандартного нормального распределения : 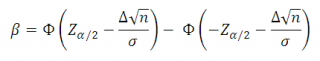
Это выражение будет работать и для Δ<0. Как видно из выражения, ошибка второго рода является функцией от α, Δ и n. В файле примера на листе Бета можно быстро рассчитать β и мощность теста в зависимости от этих параметров. Диаграмма, приведенная выше, будет автоматически перестроена.
Для заданного значения α часто строят семейство кривых, которые иллюстрируют зависимость ошибки второго рода от Δ и n. Такие кривые называются операционными характеристиками (Operating-characteristic curves). 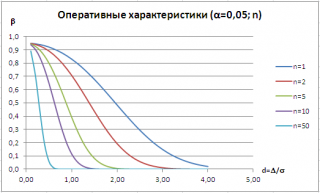
Как видно из рисунка, чем дальше истинное значение среднего от μ 0 , т.е. чем больше Δ, тем меньше ошибка второго рода. Таким образом, для заданных α и n, тест легче определит большие отклонения от среднего , чем малые (тест обладает, в данном случае, большей мощностью ). При росте n мощность теста также растет.
Кривые операционных характеристик используются для оценки размера выборки , достаточного для определения заданной разницы между истинным значением среднего μ от μ 0 с требуемой вероятностью.
В файле примера на листе ОХ создана форма для определения размера выборки , достаточного для обеспечения заданной мощности теста . 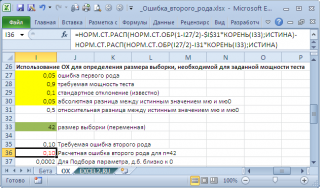
Например, Н 0 : μ 0 =20, истинное значение μ=20,05, стандартное отклонение =0,1, α=0,05. Чтобы вероятность правильно отклонить гипотезу H 0 была равна 0,9 ( мощность теста ), размер выборки должен быть 42 или более.
Примечание : Для нахождения размера выборки потребуется использование инструмента MS EXCEL Подбор параметра . 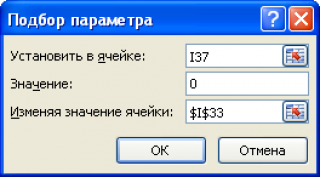
Комментарии