Проверка сложных гипотез критерием хи-квадрат Пирсона в EXCEL

Рассмотрим применение в MS EXCEL критерия хи-квадрат Пирсона для проверки сложных гипотез.

В случае проверки сложных гипотез мы задаем только форму распределения, параметры распределения, в отличие от простой гипотезы, неизвестны . Из выборки сначала нужно оценить эти неизвестные параметры, затем вычислить статистику Х ² (та же процедура, что и для простых гипотез).

Примечание : Начать знакомство с критерием согласия Пирсона Х ² (хи-квадрат) рекомендуется в отношении простых гипотез см. статью Проверка простых гипотез критерием хи-квадрат Пирсона в MS EXCEL .

В случае сложной гипотезы, p-значение , которое мы сравниваем с уровнем значимости , рассчитывается с использованием Х ² -распределения с L-k-1 степеней свободы, где k – количество оцениваемых параметров.

Если вероятность, того что случайная величина имеющая Х ² -распределение с L-k-1 степенями свободы примет значение больше вычисленной статистики Х ² , т.е. Х ² _L-k-1 >Х ² ₀ , меньше уровня значимости , то нулевая гипотеза отклоняется.

Приведем два примера проверки сложных гипотез.

Распределение Пуассона

Выдвигается гипотеза, что число дефектов в микросхемах имеет распределение Пуассона . Была исследована выборка из 50 микросхем.

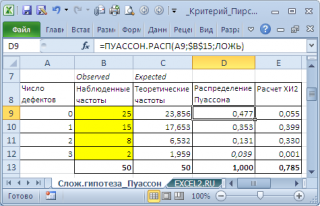
На основании выборки оценим λ ( лямбда) - единственный параметр распределения Пуассона (он равен среднему значению , см. файл примера лист Слож.гипотеза_Пуассон ). Используя оценку параметра распределения, вычислим теоретические частоты =ПУАССОН.РАСП(0;λ;ЛОЖЬ) .

Как видно из рисунка выше, случайная величина (количество дефектов в микросхеме) принимает 4 значения (четвертое значение соответствует случаю «3 и более» дефектов). Поэтому L=4, а число степеней свободы равно 4-1-1=2.

Вычислим значение статистики Х ² ₀ , а затем p -значение , чтобы сравнить его с уровнем значимости 0,05. В нашем случае нулевая гипотеза о том, что число дефектов имеет распределение Пуассона не может быть отвергнута, т.к. p -значение (0,676) больше 0,05.

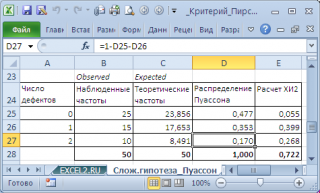
Обычно рекомендуется, чтобы каждый интервал содержал минимум 5 значений (Expected). В нашем случае это условие не соблюдается, т.к. для 3-х и более дефектов теоретическая частота меньше 2. Объединим интервалы «3 и более» и «2 дефекта» в один интервал.

Не забудем уменьшить на 1 число степеней свободы, т.к. у нас уменьшилось на 1 значение L. В итоге, p -значение также изменится (0,396), но у нас по прежнему не будет основания отвергнуть нулевую гипотезу.

Нормальное распределение

Проверим сложную гипотезу для непрерывного распределения .

Специалист отдела качества тестирует электронные устройства. Выдвигается гипотеза, что величина выходного напряжения устройства имеет нормальное распределение .

Для проверки гипотезы взята выборка из 100 устройств, среднее выборки равно 4,999 В, стандартное отклонение – 0,066 В.

В отличие от дискретного случая ( распределение Пуассона ) нам необходимо разделить непрерывный диапазон изменения случайной величины на несколько интервалов. Обычно границы интервалов выбираются таким образом, чтобы теоретическая частота была одинакова для каждого интервала.

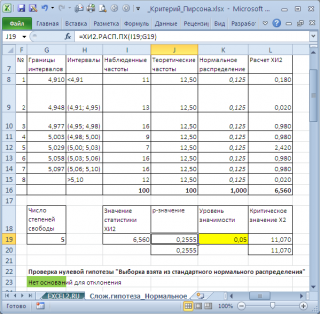
Разобьем диапазон на 8 частей. Нужно определить границы интервалов так, чтобы вероятность, что случайная величина примет значение из любого интервала была равна 1/8=0,125. Эти границы можно вычислить с помощью функции =НОРМ.ОБР(1/8*i; 4,999; 0,066) , где i – порядковый номер границы.

Число степеней свободы равно 8-2-1, т.к. с помощью выборки мы оценили 2 параметра нормального распределения (μ и σ).

Дальнейшая процедура аналогична проверке простой гипотезы (расчеты см. в файле примера лист Слож.гипотеза_Нормальное ).

СОВЕТ : О проверке других видов гипотез см. статью Проверка статистических гипотез в MS EXCEL .