Двухфакторный дисперсионный анализ без повторений в EXCEL
26 января 2019 г.
- Группы статей
- Статистический анализ
Решим задачу о сравнении средних значений нескольких выборок с использованием дисперсионного анализа в случае двух факторов без повторений (Two Factor ANOVA without Replication). Подход используемый для решения данной задачи имеет специальное название - блочный рандомизированный эксперимент (randomized block design ).
Disclaimer : Эта статья – о применении MS EXCEL для целей Дисперсионного анализа, поэтому данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения теории Дисперсионного анализа – плохая идея. Хорошая идея - найти в этой статье формулы MS EXCEL для проведения Дисперсионного анализа.
Напомним, что дисперсионный анализ (ANOVA, ANalysis Of VAriance) позволяет проверить гипотезу о равенстве средних значений выборок (взяты ли выборки из одного распределения или из разных распределений). Данная задача возникает, когда необходимо исследовать зависимость некой количественной величины Y от одной или нескольких переменных (факторов), которые мы можем контролировать (устанавливать их значения).
Перед прочтением этой статьи рекомендуется освежить в памяти Однофакторный дисперсионный анализ , в котором мы использовали полностью рандомизированный эксперимент (измерения проводились на идентичном оборудовании, выбранном в случайном порядке).
Однако, не всегда удается провести полностью рандомизированный эксперимент. Например, может быть ограничено количество идентичных единиц оборудования (устройств для проведения эксперимента), на котором проводятся измерения. Или если на условия эксперимента существенно влияют способности персонала, которые по определению не могут быть идентичными .
Задача
В компании, изготавливающей изделия путем механообработки, необходимо исследовать влияние Метода обработки поверхности детали на ее качество. Всего имеется 3 Метода обработки.
Таким образом, Метод обработки представляет собой фактор , который может принимать 3 значения (Метод 1, Метод 2, Метод 3). Назовем его Фактор А. Качество изделий будем определять по количеству дефектных изделий в партии (это будет зависимой переменной Y).
Для всех 3-х Методов потребуется применение труда операторов. Пусть в компании было принято решение, что обработка поверхности детали каждым Методом будет осуществлена 4-мя операторами. Т.е. всего потребуется 12 операторов (3 метода * 4 оператора на Метод).
Теперь спланируем эксперимент для проверки наличия влияния Метода обработки на количество дефектов.
Например, можно из 12 операторов случайным образом отобрать 4 оператора и обучить их использовать Метод 1. Затем, для Метода 2 выбрать также случайно еще 4 оператора и, наконец, 4 оператора для Метода 3. Это будет полностью рандомизированный эксперимент.
Однако, т.к. способности операторов по определению различны (не идентичны), это может сказаться на качестве эксперимента. Например, случайно, 4 самых способных операторов могут быть назначены на один из методов. В этом случае применение этого метода даст минимальное количество дефектов, что в противном случае (когда способности операторов не влияют на результат) может не соответствовать реальному положению вещей.
Чтобы исключить влияние операторов (точнее, взять это влияние под контроль) можно провести блочный рандомизированный эксперимент. Например, возьмем только 4 оператора. Каждый оператор теперь будет обучен проводить обработку поверхности всеми 3-мя методами. Порядок использования метода будет для каждого оператора случайным. Например, оператор №1 будет сначала использовать метод 2, затем 1, затем 3. А оператор №2 будет сначала использовать метод 3, затем 2, затем 1 и т.д.
Таким образом, у нас появится второй фактор, который может влиять на переменную Y. Назовем его Фактор В (оператор). В этом случае можно сказать, что каждый оператор определяет один экспериментальный блок . Таким образом, совокупность измерений (12) можно рассматривать как 3 выборки по 4 измерения (группировка по методу) или 4 блока по 3 измерения (группировка по оператору).
Данный эксперимент называется без повторений , т.к. один оператор обрабатывает каждым методом лишь одно изделие.
Отдельные, заданные значения фактора А называются его уровнями ( levels ) или испытаниями ( treatments ).
Примечание : Обратите внимание, что сначала условие задачи формулировалось как однофакторная задача: проверить влияние одного фактора (метода обработки поверхности) на качество изделия. Но, так как мы столкнулись с тем, что полностью рандомизированный эксперимент (при имеющихся в компании условиях) может исказить результат дисперсионного анализа , нам пришлось перейти к двухфакторному анализу .
Немного теории
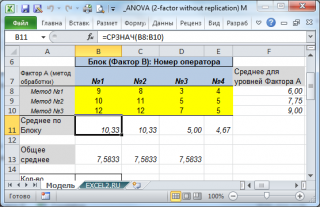
Уровни Фактора А (соответствует разным методам) будем обозначать буквой i (i изменяется от 1 до 3). В общем случае может быть а уровней фактора А. Каждому уровню фактора А соответствует одна выборка (состоит из 4-х измерений, по одному для каждого оператора).
Уровни Фактора В (соответствует разным операторам/блокам) будем обозначать буквой j (j изменяется от 1 до 4). В общем случае может быть b уровней фактора В. Каждому уровню фактора В соответствует одна выборка (состоит из 3-х измерений, по одному для каждого метода).
Непосредственно измеренные значения Y при заданном уровне фактора А (i) и уровне фактора В (j) будем обозначать y ij .
Если фактор действительно оказывает влияние на зависимую переменную Y, то при различных уровнях фактора мы должны в среднем получать различные значения Y. Другими словами, мы должны получить «заметно различающиеся» средние выборок при различных уровнях фактора А:
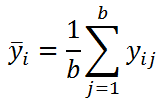
Или средние значения при различных уровнях фактора В:
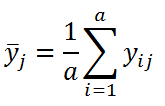
Примечание : Ниже дадим определение понятию «заметно различающиеся».
Также определим общее среднее
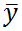 :
:
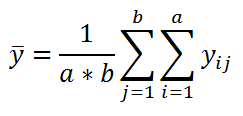
По аналогии с однофакторным дисперсионным анализом общую изменчивость (разброс) значений Y относительно общего среднего (SST = Sum of Squares Total, общая сумма квадратов) определим как сумму нескольких компонентов, в данном случае 3-х:
SST=SSA+SSB+SSE
- SSA - изменчивость обусловленная выбором метода обработки (фактор А)
- SSВ - изменчивость обусловленная выбором оператора (фактор В)
- SSE - ошибка модели (Error Sum of Squares).
SST и все 3 компонента вычисляются на основании имеющихся значений выборок (измерений):
Примечание : Вычисления SST и всех 3-х компонентов выполнены в файле примера .
Также в дисперсионном анализе используется понятие среднего квадрата отклонений (Mean Square) или сокращенно MS. Соответственно для SST имеем MST=SST/(N-1), где N=b*a является общим количеством измерений (12). Для SSA имеем MSA=SSA/(a-1), для SSВ имеем MSВ=SSВ/(b-1), для ошибки модели SSE имеем MSE=SSE/((a-1)(b-1)).
Т.е. MS имеет смысл средней изменчивости на 1 наблюдение (с некоторой поправкой). Эта поправка отражает тот факт, что MS должна вычисляться не делением SS на соответствующее количество наблюдений, а делением на число степеней свободы (degrees of freedom, DF). Например, чтобы вычислить MST, мы из N (общего количества наблюдений) должны вычесть 1, т.к. в выражении SST присутствует одно (1) среднее значение (аналогично тому, как мы делали при вычислении дисперсии ). Одна степень свободы теряется при вычислении среднего, т.к. все значения в формуле среднего связаны общим выражением (см. формулу среднего выше).
Напомним, что в однофакторном дисперсионном анализе проверяется гипотеза о равенстве средних значений этих выборок. Т.е. формулируется нулевая гипотеза Н 0 , которая утверждает, что Y не зависит от фактора и все выборки, измеренные при различных уровнях фактора, на самом деле взяты из одного распределения с общим средним.
В случае двухфакторного дисперсионного анализа формируется 2 нулевых гипотезы , обозначим их как Н 01 и Н 02 . Первая гипотеза Н 01 заключается в том, что уровень фактора А (метод обработки поверхности) не влияет на измеренные значения Y (количество дефектов), т.е. средние значения выборок, относящиеся к различным уровням Фактора А не отличаются статистически значимо (их различие может быть объяснено лишь случайностью выборок).
Вторая гипотеза Н 02 заключается в том, что уровень фактора В (номер оператора) не влияет на измеренные значения Y (количество дефектов), т.е. средние значения выборок, относящиеся к различным уровням Фактора В не отличаются статистически значимо.
Если первая нулевая справедлива , то случайная величина MSА/MSE имеет распределение Фишера с a -1 и ( a -1)( b -1) степенями свободы. Случайную величину MSА/MSE обозначим как F 1 ( тестовая статистика для двухфакторного дисперсионного анализа ). Значение отношения MSА/MSE, вычисленное на основании наблюденных значений выборок, т.е. число, обозначим как F 01 .
Если вторая нулевая справедлива , то случайная величина MSB/MSE также имеет распределение Фишера , но с b -1 и ( a -1)( b -1) степенями свободы. Случайную величину MSВ/MSE обозначим как F 2 . Конкретное значение MSВ/MSE обозначим как F 02 .
Чтобы проверить гипотезы необходимо вычислить значения тестовых статистик и сравнить их с соответствующими критическими значениями F критич , вычисленными для заданного уровня значимости альфа . Если вычисленное значение F 01 = MSА/MSE больше F 1критич , то нулевую гипотезу Н 01 об отсутствии влияния уровней Фактора А отклоняют. Аналогичные умозаключения справедливы и для Фактора В.
Проверить гипотезу Н 01 можно и через вычисление p -значения, которое представляет собой вероятность того, что случайная величина F 1 = MSА/MSE примет значение более F 01 . Далее p -значение сравнивают с уровнем значимости. Если p -значение менее уровня значимости, то нулевую гипотезу отклоняют. Действительно, если вычисленное значение F 01 получить маловероятно, то это ставит под сомнение справедливость того, что случайная величина F 1 = MSА/MSE имеет распределение Фишера с a -1 и ( a -1)( b -1) степенями свободы, а следовательно и саму нулевую гипотезу. В этом случае мы можем считать, что справедлива альтернативная гипотеза: уровни фактора А влияют на зависимую переменную Y.
Вычисления в MS EXCEL
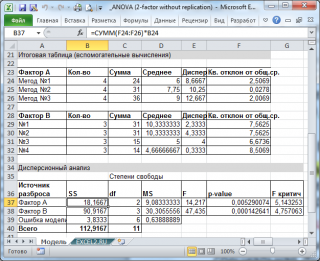
В файле примера приведено решение вышеуказанной задачи: вычислены средние значения выборок, суммы квадратов (SS), степеней свобод, средние квадратов отклонений (MS).
Для вычислений критических значений (точнее для вычисления квантилей распределения ) в MS EXCEL имеется специальная функция = F.ОБР.ПХ()
Формула для вычисления F 1критич = F.ОБР.ПХ(a-1;(a-1)(b-1);альфа)
В MS EXCEL первое p -значение (вероятность того, что случайная величина F 1 = MSА/MSE примет значение более F 01 ) можно вычислить по формуле:
= F.РАСП.ПХ((MSА/MSE; a-1;(a-1)(b-1))
Второе p -значение (вероятность того, что случайная величина F 2 = MSВ/MSE примет значение более F 02 ) можно вычислить по формуле:
=F.РАСП.ПХ((MSВ/MSE; b-1;(a-1)(b-1))
В нашей задаче p -значения получились 0,005290074 и 0,000142641, что значительно меньше обычно принимаемого в качестве уровня значимости 0,05. Таким образом, обе нулевых гипотезы отклоняются.
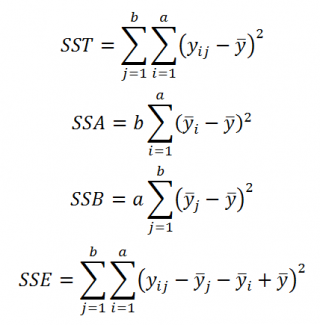

Комментарии