МНК: Экспоненциальная зависимость в EXCEL

Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.

Метод наименьших квадратов (англ. Ordinary Least Squares , OLS ) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК - МНК: Метод Наименьших Квадратов в MS EXCEL .

В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:

y=a*m ^x =a*(e ^ln(m) ) ^x = a*e ^x*ln(m) =a*e ^bx , где b= ln(m))

В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).

После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента a необходимо выполнить обратное преобразование a= EXP(A) .

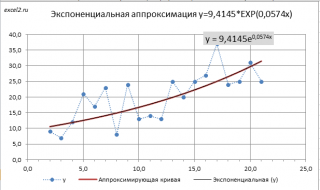
Примечание : Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда ( Экспоненциальная линия тренда ). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL .

Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больш и х по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.

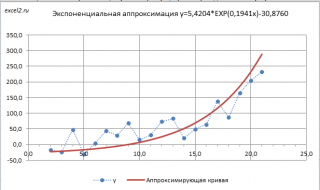
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y , ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).

Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a<0 (существует некая верхняя граница с для у ), то к линейному случаю Y=b*x+A свести задачу позволит замена переменных Y=ln(c-y) и A=ln(-a) (см. файл примера лист Экспонента3 ).

Функция РОСТ()

Еще одним способом построить линию экспоненциального тренда является использование функции РОСТ() , английское название GROWTH.

Синтаксис функции следующий:

РОСТ( известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст] )

Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент известные_значения_y ) и на массив значений переменной Х (аргумент известные_значения_x ). Функция рассчитает прогнозные значения Y для Х, указанных в аргументе новые_значения_x . Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент конст должен быть установлен равным ЛОЖЬ (или 0).

Если среди значений y есть отрицательные, то с помощью функции РОСТ() аппроксимирующую кривую построить не удастся.

Безусловно, использование функции РОСТ() часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.

Наконец, покажем как с помощью функции РОСТ() вычислить коэффициенты уравнения y= a *EXP( b *x).

Примечание : В MS EXCEL имеется специальная функция ЛГРФПРИБЛ() , которая позволяет вычислить коэффициенты уравнения y=a*EXP(b*x). Об этой функции см. ниже.

Чтобы вычислить коэффициент a (значение Y в точке Х=0) используйте формулу =РОСТ(C26:C45;B26:B45;0) . В диапазонах C26:C45 и B26:B45 должны находиться массивы значений переменной Y и X соответственно.

Чтобы вычислить коэффициент b используйте формулу:

= LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/ РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/ (МИН(B26:B45)-МАКС(B26:B45))

Функция ЛГРФПРИБЛ()

Функция ЛГРФПРИБЛ() на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты а и m уравнения y= a * m ^x.

Используя свойство степеней a ^mn =(a ^m ) ⁿ приведем уравнение экспоненциального тренда y= a *EXP( b *x)= a *e ^{b *x} = a *(e ^b ) ^x к виду y= a * m ^x, сделав замену переменной m= e ^b =EXP( b ).

Чтобы вычислить коэффициенты уравнения y= a *EXP( b *x) используйте следующие формулы:

= LN(ЛГРФПРИБЛ(C26:C45;B26:B45)) - коэффициент b

= ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2) - коэффициент a

Примечание : Функция ЛГРФПРИБЛ() , английское название LOGEST, является формулой массива, возвращающей несколько значений . Поэтому, например, для вывода коэффициентов уравнения необходимо выделить 2 ячейки в одной строке, в Строке формул ввести = ЛГРФПРИБЛ(C26:C45;B26:B45) , затем для ввода формулы вместо обычного ENTER нажать CTRL + SHIFT + ENTER .

Функция ЛГРФПРИБЛ() имеет линейный аналог – функцию ЛИНЕЙН() , которая рассмотрена в статье про простую линейную регрессию. Если 4-й аргумент этой функции ( статистика ) установлен ИСТИНА, то ЛГРФПРИБЛ() возвращает регрессионную статистику: стандартные ошибки для оценок коэффициентов регрессии, коэффициент детерминации, суммы квадратов: SSR , SSE и др.

Примечание : Особой нужды в функции ЛГРФПРИБЛ() нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y= a * m ^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y= a *EXP( b *x).