Перестановки без повторений: Комбинаторика в EXCEL

Подсчитаем в MS EXCEL количество перестановок из n элементов. С помощью формул выведем на лист все варианты перестановок (английский перевод термина: permutation).

Перестановкой множества из n элементов называется расположение элементов в определенном порядке.

Элементами множества могут быть числа, буквы и вообще любые объекты. Главное, чтобы эти элементы были различными. Т.к. любому объекту можно сопоставить число, то для Перестановок обычно используют конечное множество целых чисел, например, {1; 2; 3; 4; 5}. Хотя множества из букв также можно часто встретить в литературе. Например, все различные Перестановки множества из трех элементов {a, b, c} – это abc , acb , bac , bca , cab , cba .

Число Перестановок n элементов равно n! (факториал).

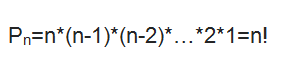
Для вычисления факториала в MS EXCEL есть функция =ФАКТР() , английский вариант FACT(). Понятно, что число перестановок растет очень быстро с ростом n: для n=7 число перестановок равно 5040. Справедливости ради, нужно отметить, что зачастую сами варианты перестановок находить не требуется, главное – найти их количество.

Примечание : Перестановки можно считать частным случаем размещений при n=k (см. статью Размещения без повторений: Комбинаторика в MS EXCEL ). Поэтому для вычисления количества перестановок можно использовать функцию ПЕРЕСТ() . Для n=7 число Перестановок вычисляется по формуле =ПЕРЕСТ(7;7)

Примечание : О Перестановках с повторениями (с возвращением элементов обратно во множество, из которого они берутся, после выборки каждого элемента) можно прочитать в статье Перестановки с повторениями: Комбинаторика в MS EXCEL .

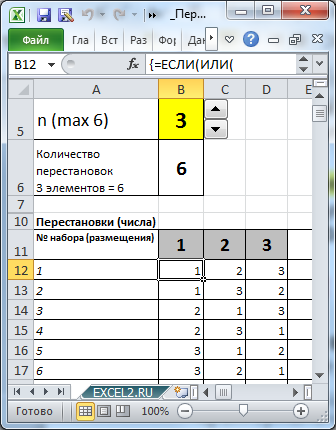
В файле примера создана универсальная формула для вывода всех Перестановок для заданного n. Например, для n=3.

Задача

6 машин разных марок участвуют в гонках на выживание: LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo. Определить число возможных вариантов распределения мест между всеми участниками.

Нам нужно определить число перестановок 6 машин на 6-и местах. Т.е. n=6. Оказывается, что таких перестановок 720: =ПЕРЕСТ(6;6) или 6! =ФАКТР(6)

Воспользуемся файлом примера , чтобы найти все варианты перестановок.

Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …

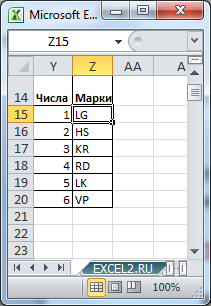
Введя в ячейке В5 значение 6, определим все варианты расстановок машин на занятых ими в гонке местах.

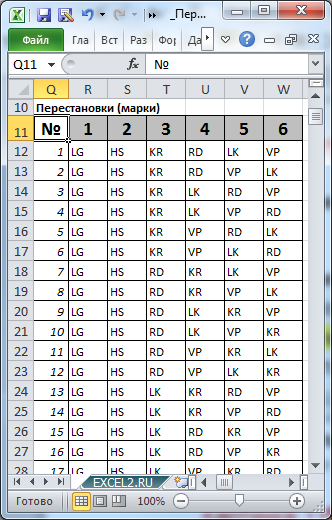
Примечание : О Размещениях можно прочитать в статье Размещения без повторений: Комбинаторика в MS EXCEL , а о Сочетаниях в статье Сочетания без повторений: Комбинаторика в MS EXCEL .

Перебор всех возможных перестановок может потребоваться для решения различных задач (см. статью Поиск решения MS EXCEL (6.2). Задача коммивояжера (полный граф, нелинейная модель) и Вычисление определителя матрицы в MS EXCEL ).

Инверсии перестановок

Для каждой перестановки a 1, a 2, a 3,..., a n из n целых чисел 1, 2, 3, ..., n , инверсией называется пара ( a i, a j) если для i < j выполняется a i > a j. Число инверсией в перестановке показывает насколько перестановка является "несортированной" по возрастанию.

Например, число инверсий в перестановке 1, 2, 3, 4 равно 0 (перестановка из 4-х целых чисел отсортирована по возрастанию от 1 до 4), а число инверсий в перестановке 4, 3, 1, 2 равно 5, т.к.:

• первый элемент (i=1) равен 4 и он больше 3-х чисел (с j=2, 3, 4), которые расположены правее (4>3, 4>1, 4>2), т.е. мы имеем 3 инверсии;
• второй элемент (i=2) равен 3 и он больше 2-х чисел (с j=3, 4), которые расположены правее (3>1, 3>2), т.е. мы имеем еще 2 инверсии;
• так третий элемент (i=3) равен 1 и он меньше числа с j=4, которое расположено правее (1<2), то эта пара не является инверсией. Т.е. у перестановки 4, 3, 1, 2 число инверсий равно 3+2+0=5.

В файле примера для каждой Перестановки подсчитывается число инверсией.

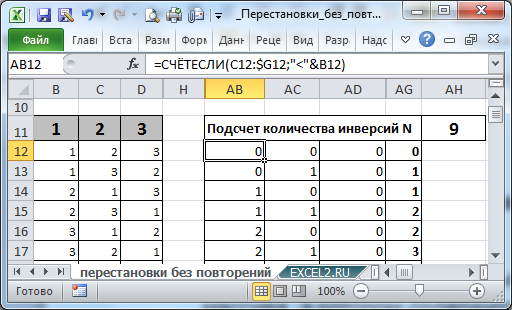
Инверсии перестановок, например, используются при вычислении определителя матрицы (см. статью Вычисление определителя матрицы в MS EXCEL ).