Равномерное дискретное распределение в EXCEL

Рассмотрим Равномерное дискретное распределение, построим график функции распределения, вычислим среднее значение и дисперсию. Сгенерируем случайные значения (выборку) с помощью функции MS EXCEL СЛУЧМЕЖДУ() . На основании выборки оценим среднее и стандартное отклонение распределения.

Равномерное дискретное распределение (англ. Discrete uniform distribution) имеет место, например, при подбрасывании симметричной монеты. Пусть если выпал «орёл», то случайная величина принимает значение 1, если выпала «решка» - то 0. Т.к. вероятность наступления событий одинакова и всего 2 возможных исхода, то вероятность случайной величины принять значение 1 (или 0) равна 1/2=0,5.

Распределение называется равномерным, т.к. вероятность любого исхода одинакова.

Примечание : В данном случае, когда возможно всего 2 исхода, равномерное распределение является частным случаем Распределения Бернулли с параметром p = q =1- p =0,5.

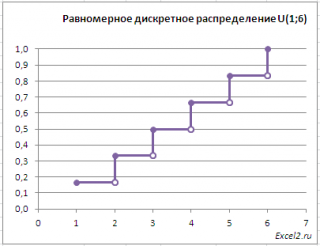
Другой пример. Результат бросания симметричной игральной кости является равномерной дискретной случайной величиной , т.к. количество точек на грани кубика принимает одно из 6 равновероятных значений. Вероятность выпадения каждой из шести граней равна 1/6.

Для этого примера функция распределения будет выглядеть следующим образом.

Примечание : Для построения графика использованы идеи из статьи про ступенчатый график .

СОВЕТ : Подробнее о Функции распределения см. статью Функция распределения и плотность вероятности в MS EXCEL .

Математическое ожидание и дисперсия

В файле примера на листе График приведен расчет математического ожидания по формуле =(a+b)/2.

Дисперсия (квадрат стандартного отклонения) для равномерного дискретного распределения может быть вычислена по формуле =((b-a+1)^2-1)/12.

Генерация случайных значений

Случайные числа, имеющие равномерное дискретное распределение , можно сгенерировать с помощью функции MS  EXCEL СЛУЧМЕЖДУ() . В функции можно задать нижнюю и верхнюю границу интервала [a; b]. Функцией будут сгенерированы целые случайные числа из указанного интервала (см. файл примера лист Генерация ).

Обратите внимание, что массив случайных чисел, сгенерированных с помощью функции СЛУЧМЕЖДУ() , автоматически обновится при пересчете листа. Пересчет листа в MS EXCEL производится при вводе нового значения в ячейку или при нажатии клавиши F9 .

Примечание : Подробнее про функцию СЛУЧМЕЖДУ() см. статью Функция СЛУЧМЕЖДУ() - Случайное число из заданного интервала в MS EXCEL .

Чтобы сгенерировать нецелые случайные числа, например из интервала [1,1; 2,5], необходимо записать формулу = СЛУЧМЕЖДУ(1,1*10;2,5*10)/10 .

Множитель 10 отражает тот факт, что нецелые случайные числа будут сгенерированы с точностью до десятых. Если интервал задан с точностью до сотых, то нужно использовать множитель 100.

Как видно из формулы - границы интервала также могут быть нецелыми числами. Хотя, конечно, можно сгенерировать числа, например, с точностью до сотых с помощью формулы = СЛУЧМЕЖДУ(10*100;20*100)/100 . В этом случае случайные числа будут принадлежать интервалу [10;20] и иметь вид 10,37; 16,08; 15,43 и т.д.

Оценка среднего и стандартного отклонения

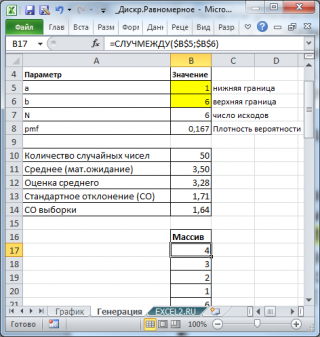
Сгенерируем 50 чисел (выборку) и разместим их в диапазоне B17:B66 . Нижнюю и верхнюю границу интервала возьмем [1; 6] и разместим их в диапазоне B5:B6 .

Математическое ожидание этого распределения =(B5+B6)/2 и равно (6+1)/2=3,5. Стандартное отклонение распределения равно = КОРЕНЬ(((B6-B5+1)^2-1)/12) =1,71

Чтобы оценить математическое ожидание воспользуемся значениями выборки =СУММ(B17:B66)/СЧЁТ(B17:B66) .

Оценить стандартное отклонение можно с помощью формулы =СТАНДОТКЛОН.В(B17:B66) в MS EXCEL 2010 или = СТАНДОТКЛОН(B17:B66) для более ранних версий.

Чтобы оценить дисперсию используйте формулу =ДИСП.В(B17:B66) в MS EXCEL 2010 или =ДИСП(B17:B66) для более ранних версий. Также можно использовать формулу =СТАНДОТКЛОН.В(B17:B66)^2 .

СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .