Аннуитет. Обзор функций EXCEL

В статье рассмотрены финансовые функции ПЛТ() , ОСПЛТ() , ПРПЛТ() , КПЕР() , СТАВКА() , ПС() , БС() , а также ОБЩДОХОД() и ОБЩПЛАТ() , которые используются для расчетов параметров аннуитетной схемы.

Данная статья входит в цикл статей о расчете параметров аннуитета. Перечень всех статей на нашем сайте об аннуитете размещен здесь .

В этой статье содержится небольшой раздел о теории аннуитета, краткое описание функций аннуитета и их аргументов, а также ссылки на статьи с примерами использования этих функций.

Немного теории

Аннуитет (иногда используются термины «рента», «финансовая рента») представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени (например, когда платежи производятся ежегодно равными суммами).

Каждый элемент такого денежного потока называется членом аннуитета , а величина постоянного временного интервала между двумя его последовательными элементами называется периодом аннуитета . В широком смысле, аннуитетом может называться как сам финансовый инструмент, так и сумма периодического платежа. Исторически вначале рассматривались равные ежегодные денежные поступления (период между платежами принимался равным одному году), что и послужило основой для именования денежного потока аннуитетом («год» на латинском языке — anno). В дальнейшем, в качестве периода стал выступать любой промежуток времени, но прежнее название сохранилось. Сейчас период аннуитета чаще всего равен одному месяцу.

Аннуитетную схему банки часто используют при кредитовании . Эта схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), т.е. равными суммами через равные промежутки времени , которые включают как выплату основного долга, так и процентный платеж за пользование кредитом.

На картинке ниже приведен пример погашения кредита (100 000 руб.) ежемесячными платежами в течение 5 лет при ставке 15%. Для погашения тела кредита и начисленных процентов потребуется произвести 60 платежей (5 лет*12мес в году). Сумма ежемесячного платежа = 2378,99руб. См. файл примера Лист Аннуитет (ПЛТ) . Как видно из графика платежей, банк в первые периоды получает платежи, идущие на погашение %, а тело кредита сокращается медленно (см. статью Сравнение графиков погашения кредита дифференцированными и аннуитетными платежами в MS EXCEL ).

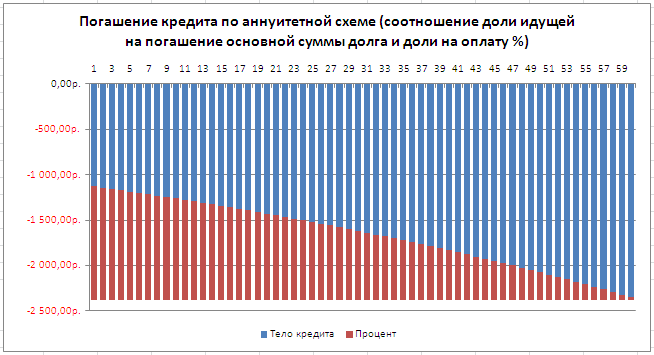
Если каждый элемент аннуитета имеет место в конце соответствующего периода, аннуитет называется аннуитетом постнумерандо (Ordinary Annuity); если в начале периода — аннуитетом пренумерандо (Annuity Due). Обычно используется аннуитет постнумерандо.

Примечание . В функциях MS EXCEL для указания типа аннуитета предусмотрен специальный необязательный параметр [тип] . По умолчанию тип =0  (выплаты в конце периода), что соответствует аннуитету постнумерандо. Если тип =1, то предполагается аннуитет пренумерандо (выплаты в начале периода).

Часто в расчетах используют понятие аннуитетный коэффициент (А):

A = -Ставка * (1+ Ставка)^Кпер / (1-(1+ Ставка)^ Кпер ) / (1+ Ставка*Тип)

где: Ставка — процентная ставка за период; Кпер — общее количество периодов выплаты; Тип – для аннуитета постнумерандо Тип=0, для пренумерандо Тип=1.

Чтобы вычислить член аннуитета (величину регулярного платежа) нужно использовать формулу =А*ПС, где ПС – это начальная сумма кредита. Специфика аннуитета (равенство денежных поступлений) позволяет вывести стандартизованные формулы, существенно упрощающие счетные процедуры. Об этих формулах и об их использовании в MS EXCEL и пойдет речь ниже.

Параметры функций аннуитета

Финансовые функции ПЛТ() , ОСПЛТ() , ПРПЛТ() , КПЕР() , СТАВКА() , БС() , ПС() , а также ОБЩДОХОД() и ОБЩПЛАТ() тесно связаны между собой, т.к. все они вычисляют параметры аннуитета и, соответственно, используют один и тот же набор аргументов. В этом можно убедиться, перечислив все функции вместе с аргументами:

ПЛТ(ставка; кпер; пс; [бс]; [тип]) ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) ПРПЛТ(ставка; период; кпер; пс; [бс]; [тип]) КПЕР(ставка; плт; пс; [бс]; [тип]) СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение]) БС(ставка; кпер; плт; [пс]; [тип]) ПС(ставка; кпер; плт; [бс]; [тип])

ПЛТ (английское название функции: PMT, от слова payment ). Регулярный платеж, осуществляемый каждый период. Платеж – постоянная величина, она не меняется в течение всего срока аннуитета. Ставка (англ.: RATE, interest). Процентная ставка за период , чаще всего за год или за месяц. Обычно задается через годовую ставку, деленную на количество периодов в году. При годовой ставке 10% месячная ставка составит 10%/12. Ставка не изменяется в течение всего срока аннуитета. Кпер (англ.: NPER). Общее число периодов платежей по аннуитету . Если кредит взят на 5 лет, а выплаты производятся ежемесячно, то всего 60 периодов (12 мес. в году * 5 лет) Бс (англ.: FV, future value). Будущая стоимость в конце срока аннуитета (по истечении числа периодов Кпер). Бс - требуемое значение будущей стоимости или остатка средств после последней выплаты. Например, в случае расчета аннуитетного платежа для полной выплаты ссуды к концу срока Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена. Пс (англ.: PV, present value). Приведенная стоимость , т.е. стоимость приведенная к определенному моменту (часто к текущему, т.е. настоящему времени). Если взят кредит и производятся регулярные выплаты по аннуитетной схеме, то Приведенная стоимость – это сумма кредита. Если планируется регулярно вносить равновеликие платежи на счет в банке (и период начисления % совпадает с периодом платежей), то Приведенную стоимость также нужно указывать = 0. Тип (англ.: type). Число 0 или 1, обозначающее, когда должна производиться выплата (и соответственно начисление процентов). 0 – в конце периода, 1 – в начале. Подробнее см. раздел Немного теории в начале статьи о постнумерандо и пренумерандо или статьи с примерами, указанные выше.

Все 6 аргументов (параметров аннуитета) связаны между собой выражением:

поэтому каждый из них может быть вычислен при условии, если заданы остальные параметры. Функции аннуитета помогают пользователю упростить вычисления, но все они основаны на Формуле 1.

Примечание . Формула 1 работает, если Ставка не равна 0. Если ставка равна 0, то вместо Формулы 1 действует гораздо более простое выражение: ПЛТ * Кпер + ПС + БС = 0 (в этом случае схема платежей перестает быть аннуитетом и превращается в беспроцентную ссуду).

О направлениях денежных потоков и знаках ПС, БС и ПЛТ

Вышеуказанная Формула 1 предполагает, что знаки денежных потоков (+/-) указываются с учетом их направления. Например, банк выдал кредит (ПС>0), клиент банка ежемесячно вносит одинаковый платеж (ПЛТ<0). Т.е. имеет место 2 направления движения денег: от банка к клиенту (ПС) и в банк от клиента (ПЛТ). Если схема погашения кредита учитывает единовременную выплату в конце погашения, то БС<0, т.к. этот платеж, как и ПЛТ направлен в банк от клиента . Функции MS EXCEL также учитывают направления платежей, поэтому функция ПЛТ() возвращает отрицательные значения, если ПС>0.

Тождество аннуитета

Если Тип=0, то для функций MS EXCEL справедливо тождество: ОБЩДОХОД(за все периоды) + ПС + БС = 0

Это тождество можно переписать в другом виде: СУММ(ОСПЛТ()) + ПС + БС = 0. В случае использования аннуитетной схемы погашения кредита (сумма кредита =ПС), выражение СУММ(ОСПЛТ()) вычисляет общую сумму платежей, идущих на оплату основной суммы долга (тело кредита). В случае полного погашения кредита БС=0, а тождество превращается в ПС=-СУММ(ОСПЛТ()).

Функции MS EXCEL для расчета параметров аннуитета

Теперь кратко рассмотрим функции MS EXCEL. Для того, чтобы нижесказанное было понятным, необходимо предварительно ознакомиться с теорией аннуитета, понятиями Будущая и Приведенная стоимость.

Функция ПЛТ(ставка; кпер; пс; [бс]; [тип]) рассчитывает величину регулярного платежа на основе заданных 5 аргументов.

Примечание . Английский вариант функции: PMT(rate, nper, pv, [fv], [type]), т.е. PayMenT – платеж.

Примечание . Вышеуказанные функции входят в надстройку «Пакет анализа». Если функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (с версии MS EXCEL 2007 надстройка «Пакет анализа» включена по умолчанию).

Для понимания работы формулы приведем эквивалентное ей выражение для расчета платежа:

Формула 2 есть не что иное, как решение Формулы 1 относительно параметра ПЛТ.

Примечание. В файле примера на листе Аннуитет (без ПЛТ) приведен расчет ежемесячных платежей без использования финансовых функций EXCEL.

Если процентная ставка = 0, то Формула 2 упростится до =(ПС + БС)/Кпер

Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 заметно упрощается:

В случае применения схемы аннуитета для выплаты ссуды платеж включает денежную сумму в счет погашения части ссуды и сумму для оплаты начисленных за прошедший период процентов, поэтому функция ПЛТ() связана с ОСПЛТ() и ПРПЛТ() соотношением ПЛТ = ОСПЛТ + ПРПЛТ (для каждого периода).

Примечание . В файле примера на листе Зависимости ПЛТ() приведены графики: Зависимость суммы платежа от размера ссуды, Зависимость суммы платежа от ставки, Зависимость суммы платежа от срока ссуды. Также в файле примера приведены некоторые задачи.

Функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) используется для вычисления регулярных сумм идущих на погашение основной суммы долга практически с теми же аргументами, что и ПЛТ() . Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент период , который определяет к какому периоду относится сумма.

Примечание . Английский вариант функции: PPMT(rate, per, nper, pv, [fv], [type]), т.е. Principal Payment – платеж основной части долга.

В случае применения схемы аннуитета для выплаты ссуды для каждого периода действует равенство: ОСПЛТ =ПЛТ – ПРПЛТ, т.к. платеж включает сумму в счет погашения части ссуды (ОСПЛТ) и сумму для оплаты начисленных за прошедший период процентов (ПРПЛТ). Сумму, идущую на погашение основной суммы долга также можно вычислить, зная  величину платежа (ПЛТ), период (Период), общее количество периодов (Кпер) и ставку (СТАВКА):

ОСПЛТ=ПЛТ*(1+СТАВКА)^(Период-Кпер-1)

Вышеуказанная формула работает при БС=0. При ТИП=1 (платеж в начале периода) и n=1 (первый платеж), ПРПЛТ=ПЛТ Если БС<>0, то формула усложнится:

Функцию ОСПЛТ() часто применяют при составлении графика платежей по аннуитетной схеме (см. Выплата основной суммы долга в аннуитетной схеме. Расчет в MS EXCEL )

Примечание . В файле примера на листе Аннуитет (без ПЛТ) определена аналитическая зависимость суммы идущей на погашение долга от номера периода.

Функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип]) используется для вычисления регулярных сумм идущих на погашение процентов за ссуду используется с теми же аргументами, что и ОСПЛТ() .

Примечание. Английский вариант функции: IPMT(rate, per, nper, pv, [fv], [type]), т.е. Interest Payment – выплата процентов.

В случае применения схемы аннуитета для выплаты ссуды для каждого периода действует равенство: ПРПЛТ =ПЛТ – ОСПЛТ

Сумму, идущую на погашение процентов за ссуду, можно вычислить зная: величину платежа (ПЛТ), период (Период), общее количество периодов (Кпер) и ставку (СТАВКА):

ПРПЛТ =ПЛТ*(1-(1+СТАВКА)^(Период-Кпер-1))

Вышеуказанная формула работает при БС=0. При ТИП=1 (платеж в начале периода) и n=1 (первый платеж), ПРПЛТ=0 Если БС<>0, то формула усложнится:

Соотношение выплат основной суммы долга и на погашение начисленных процентов за период хорошо демонстрирует график, приведенный в файле примера .

Функцию ПРПЛТ() часто применяют при составлении графика платежей по аннуитетной схеме (см. Аннуитет. Расчет в MS EXCEL выплаченных процентов за период ).

Функция КПЕР(ставка; плт; пс; [бс]; [тип]) позволяет вычислить количество периодов, через которое текущая сумма вклада (пс) станет равной заданной сумме (бс) при известной процентной ставке за период (ставка) и известной величине пополнения вклада (плт). При этом предполагается, сумма пополнения вклада вносится регулярно в каждый период, тогда же происходит и начисление процентов. Сумма пополнения вклада может быть равна 0 (вклад не пополняется, рост вклада осуществляет только за счет капитализации процентов). Бс (будущая стоимость) может быть =0 или опущена. Также функцию КПЕР() можно использовать для определения количества периодов, необходимых для погашения долга по ссуде (погашение осуществляется регулярно равными платежами, ставка не изменяется весь срок, на который выдана ссуда, процент начисляется каждый период на остаток ссуды).

Примечание . Английский вариант функции: NPER(rate, pmt, pv, [fv], [type]), т.е. Number of Periods – число периодов.

Эквивалентная формула для расчета платежа:

Если ставка равна 0, то: Кпер = (Пс + Бс) /ПЛТ

Подробнее про функцию можно прочитать в статье Аннуитет. Расчет в MS EXCEL количества периодов .

Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение]) возвращает процентную ставку по аннуитету.

Примечание . Английский вариант функции: RATE(nper, pmt, pv, [fv], [type], [guess]), т.е. Number of Periods – число периодов.

]]> Вот что написано на сайте MS ]]> : Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1. Если постараться решить это уравнение относительно параметра Ставка, то мы получим степенное уравнение (степень уравнения и, соответственно, число его корней будет зависеть от значения Кпер). В отличие от других параметров ПЛТ, БС, ПС и Кпер, найти универсальное решение этого уравнения для всевозможных степеней невозможно, поэтому приходится использовать метод итераций (по сути, метод подбора ). Чтобы облегчить поиск Ставки методом итераций, используется аргумент Предположение. Предположение - это приблизительное значение Ставки, т.е. прогноз на основании нашего знания о задаче. Если значение предположения опущено, то оно полагается равным 10 процентам. Значение Предположение также полезно в случае , если имеется несколько решений уравнения – в этом случае находится значение Ставки ближайшее к Предположению .

Подробнее про функцию можно прочитать в статье Аннуитет. Определяем процентную ставку в MS EXCEL .

Функция БС(ставка; кпер; плт; [пс]; [тип]) возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки. Например, если у Вас сейчас на банковском счете сумма ПС (ПС м.б. =0) и вы ежемесячно вносите одну и туже сумму ПЛТ, то функция вычислит остаток на Вашем банковском счете через Кпер месяцев (предполагается, что капитализация процентов происходит также ежемесячно с процентной ставкой равной величине СТАВКА).

Примечание . Английский вариант функции: FV(rate, nper, pmt, [pv], [type]), т.е. Future Value – будущая стоимость.

Вычисления в функции БС() производятся по этой формуле:

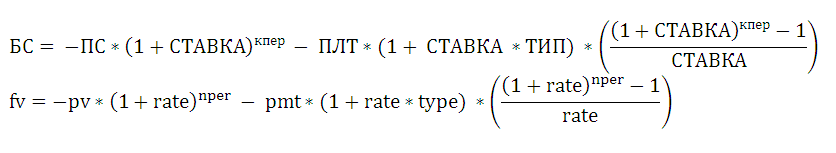
Если СТАВКА =0, то Будущую стоимость можно определить по формуле БС= - ПЛТ * Кпер + ПС

Подробнее про функцию можно прочитать в статье Аннуитет. Определяем в MS EXCEL Будущую Стоимость .

Функция ПС(ставка; кпер; плт; [бс]; [тип]) возвращает приведенную (к текущему моменту) стоимость инвестиций . Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на настоящий момент равноценна ряду будущих регулярных выплат ПЛТ за количество периодов Кпер. Также предполагается, что капитализация процентов происходит также регулярно с процентной ставкой равной величине СТАВКА.

Примечание . Английский вариант функции: PV(rate, nper, pmt, [fv], [type]), т.е. Present Value – будущая стоимость.

Вычисления в функции ПС() производятся по этой формуле:

Если СТАВКА =0, то Приведенную стоимость можно определить по формуле ПС=-БС-ПЛТ*Кпер

Подробнее про функцию можно прочитать в статье Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость

Функции ОБЩДОХОД() и ОБЩПЛАТ() Аргументы функций ОБЩДОХОД() и ОБЩПЛАТ() несколько отличаются от рассмотренных выше. Но на самом деле разница только в их названии: кол_пер – это кпер; нз – это пс. Нач_период и кон_период – это «начальный период» и «конечный период».

Функция ОБЩДОХОД(ставка; кол_пер; нз; нач_период; кон_период; тип) возвращает кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами ( нач_период и кон_период ).

Примечание . Английский вариант функции:  CUMPRINC(rate, nper, pv, start_period, end_period, type) returns the CUMulative PRincipal paid for an investment period with a Constant interest rate.

Подробнее про функцию можно прочитать в статье Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга .

Функция ОБЩПЛАТ(ставка; кол_пер; нз; нач_период; кон_период; тип) возвращает кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат ( нач_период и кон_период ).

Примечание . Английский вариант функции: CUMIPMT(rate, nper, pv, start_period, end_period, type) returns the CUMulative Interest paid on a loan between start_period and end_period.

Подробнее про функцию можно прочитать в статье Аннуитет. Расчет в MS EXCEL выплаченных процентов за период .

Общую сумму выплат по займу между двумя периодами (Нач_период и кон_период) можно найти сложив результаты возвращаемые ОБЩПЛАТ() и ОБЩДОХОД() с одинаковыми аргументами, что эквивалентно ПЛТ*(кон_период - Нач_период+1).