Аннуитет. Расчет периодического платежа в EXCEL. Погашение ссуды (кредита, займа)

Рассчитаем в MS EXCEL сумму регулярного аннуитетного платежа при погашении ссуды. Сделаем это как с использованием функции ПЛТ() , так и впрямую по формуле аннуитетов. Также составим таблицу ежемесячных платежей с расшифровкой оставшейся части долга и начисленных процентов.

При кредитовании банки наряду с дифференцированными платежами часто используют аннуитетную схему погашения . Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат.

Задача1

Определить величину ежемесячных равновеликих выплат по ссуде, размер которой составляет 100 000 руб., а процентная ставка составляет 10% годовых. Ссуда взята на срок 5 лет.

Разбираемся, какая информация содержится в задаче:

1. Заемщик ежемесячно должен делать платеж банку. Этот платеж включает: сумму в счет погашения части ссуды и сумму для оплаты начисленных за прошедший период процентов на остаток ссуды ;
2. Сумма ежемесячного платежа (аннуитета) постоянна и не меняется на протяжении всего срока, так же как и процентная ставка. Также не изменяется порядок платежей – 1 раз в месяц;
3. Сумма для оплаты начисленных за прошедший период процентов уменьшается каждый период, т.к. проценты начисляются только на непогашенную часть ссуды;
4. Как следствие п.3 и п.1, сумма, уплачиваемая в счет погашения основной суммы ссуды, увеличивается от месяца к месяцу.
5. Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
6. Проценты начисляются в конце каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0. Платеж должен производиться также в конце каждого периода;
7. Процент за пользование заемными средствами в месяц (за период) составляет 10%/12 (ставка);
8. В конце срока задолженность должна быть равна 0 (БС=0).

Расчет суммы выплаты по ссуде за один период, произведем сначала с помощью финансовой функции MS EXCEL ПЛТ() .

Примечание . Обзор всех функций аннуитета в статье найдете здесь .

Эта функция имеет такой синтаксис: ПЛТ(ставка; кпер; пс; [бс]; [тип]) PMT(rate, nper, pv, [fv], [type]) – английский вариант.

Примечание : Функция ПЛТ() входит в надстройку «Пакет анализа». Если данная функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (в MS EXCEL 2007/2010 надстройка «Пакет анализа» включена по умолчанию).

Первый аргумент – Ставка. Это процентная ставка именно за период, т.е. в нашем случае за месяц. Ставка =10%/12 (в году 12 месяцев). Кпер – общее число периодов платежей по аннуитету, т.е. 60 (12 мес. в году*5 лет) Пс - Приведенная стоимость всех денежных потоков аннуитета. В нашем случае, это сумма ссуды, т.е. 100 000. Бс - Будущая стоимость всех денежных потоков аннуитета в конце срока (по истечении числа периодов Кпер). В нашем случае Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена. Если этот параметр опущен, то он считается =0. Тип - число 0 или 1, обозначающее, когда должна производиться выплата. 0 – в конце периода, 1 – в начале. Если этот параметр опущен, то он считается =0 (наш случай).

Примечание : В нашем случае проценты начисляются в конце периода. Например, по истечении первого месяца начисляется процент за пользование ссудой в размере (100 000*10%/12), до этого момента должен быть внесен первый ежемесячный платеж. В случае начисления процентов в начале периода, в первом месяце % не начисляется, т.к. реального пользования средствами ссуды не было (грубо говоря % должен быть начислен за 0 дней пользования ссудой), а весь первый ежемесячный платеж идет в погашение ссуды (основной суммы долга).

Решение1 Итак, ежемесячный платеж может быть вычислен по формуле =ПЛТ(10%/12; 5*12; 100 000; 0; 0) , результат -2 107,14р. Знак минус показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые банк дал нам, -2107,14 – это деньги, которые мы возвращаем банку .

Альтернативная формула для расчета платежа (общий случай): =-(Пс*ставка*(1+ ставка)^ Кпер /((1+ ставка)^ Кпер -1)+ ставка /((1+ ставка)^ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка +1);1)

Если процентная ставка = 0, то формула упростится до =(Пс + Бс)/Кпер Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 также упрощается:

Вышеуказанную формулу часто называют формулой аннуитета (аннуитетного платежа) и записывают в виде А=К*S, где А - это аннуитетный платеж (т.е. ПЛТ), К - это коэффициент аннуитета, а S - это сумма кредита (т.е. ПС). K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1), где i=ставка за период (т.е. Ставка), n - количество периодов (т.е. Кпер). Напоминаем, что выражение для K справедливо только при БС=0 (полное погашение кредита за число периодов Кпер) и Тип=0 (начисление процентов в конце периода).

Таблица ежемесячных платежей

Составим таблицу ежемесячных платежей для вышерассмотренной задачи.

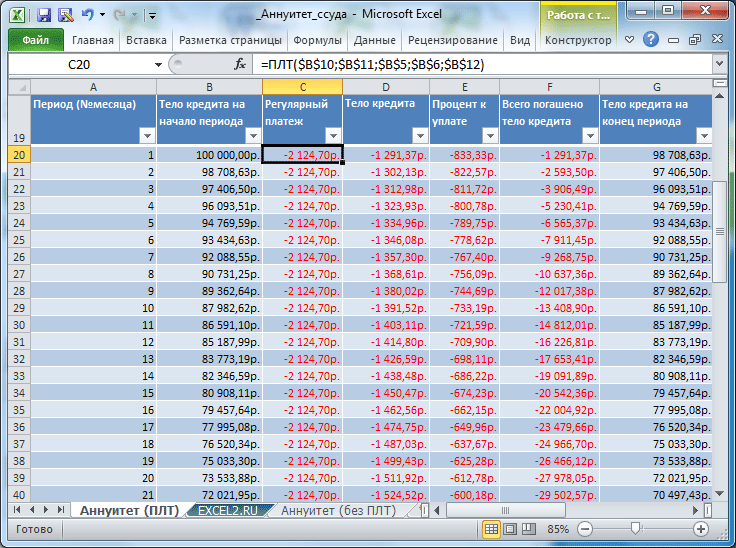
Для вычисления ежемесячных сумм идущих на погашение основной суммы долга используется функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) практически с теми же аргументами, что и ПЛТ() (подробнее см. статью Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга ). Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент период , который определяет к какому периоду относится сумма.

Для вычисления ежемесячных сумм идущих на погашение процентов за ссуду используется функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип]) с теми же аргументами, что и ОСПЛТ() (подробнее см. статью Аннуитет. Расчет в MS EXCEL выплаченных процентов за период ).

Примечание . Для определения суммы переплаты по кредиту (общей суммы выплаченных процентов) используйте функцию ОБЩПЛАТ() , см. здесь .

Конечно, для составления таблицы ежемесячных платежей можно воспользоваться либо ПРПЛТ() или ОСПЛТ() , т.к. эти функции связаны и в любой период: ПЛТ= ОСПЛТ + ПРПЛТ

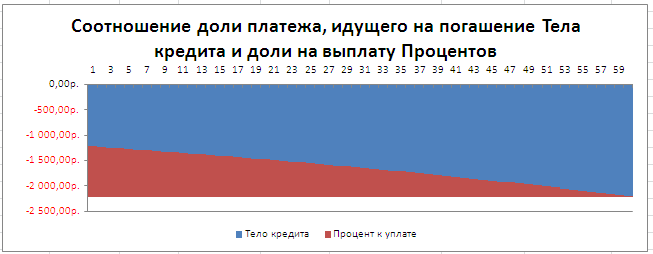
Соотношение выплат основной суммы долга и начисленных процентов хорошо демонстрирует график, приведенный в файле примера .

Примечание . В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад показано как рассчитать величину регулярной суммы пополнения вклада, чтобы накопить желаемую сумму.

График платежей можно рассчитать без использования формул аннуитета. График приведен в столбцах K:P файла примера лист Аннуитет (ПЛТ) , а также на листе Аннуитет (без ПЛТ) . Также тело кредита на начало и конец периода можно рассчитать с помощью функции ПС и БС (см. файл примера лист Аннуитет (ПЛТ), столбцы H:I ).

Задача2

Ссуда 100 000 руб. взята на срок 5 лет. Определить величину ежеквартальных равновеликих выплат по ссуде, чтобы через 5 лет невыплаченный остаток составил 10% от ссуды. Процентная ставка составляет 15% годовых.

Решение2 Ежеквартальный платеж может быть вычислен по формуле =ПЛТ(15%/12; 5*4; 100 000; -100 000*10%; 0) , результат -6 851,59р. Все параметры функции ПЛТ() выбираются аналогично предыдущей задаче, кроме значения БС, которое = -100000*10%=-10000р., и требует пояснения. Для этого вернемся к предыдущей задаче, где ПС = 100000, а БС=0. Найденное значение регулярного платежа обладает тем свойством, что сумма величин идущих на погашение тела кредита за все периоды выплат равна величине займа с противоположным знаком. Т.е. справедливо равенство: ПС+СУММ(долей ПЛТ, идущих на погашение тела кредита)+БС=0: 100000р.+(-100000р.)+0=0. То же самое и для второй задачи: 100000р.+(-90000р.)+БС=0, т.е. БС=-10000р.