Аннуитет. Определяем в EXCEL Будущую Стоимость

Определим Будущую стоимость инвестиции в случае аннуитета. Под инвестицией будем понимать как регулярные взносы, так и начальный взнос. Для этого будем использовать функцию БС() . Также выведем альтернативную формулу для расчета Будущей стоимости.

Будущая стоимость (Future Value), является суммой, в которую в будущем превратится определенная сумма денег, инвестированная ранее под известную процентную ставку. Она рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Будущей стоимости, также как и Текущей стоимости важен, так как, платежи, осуществленные в различные моменты времени, можно сопоставлять (сравнивать, складывать, вычитать) лишь после приведения их к одному временному моменту. Будущая стоимость инвестиций зависит от того, каким методом начисляются проценты: простые проценты , сложные проценты или аннуитет .

В MS EXCEL Будущая стоимость для аннуитета и для сложных процентов рассчитывается функцией БС() .

Примечание : в случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов (не аннуитет) используется функция БЗРАСПИС() .

Использование функции БС() в случае накопления вклада

Функция БС(ставка; кпер; плт; [пс]; [тип]) возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки. Например, если у Вас сейчас на банковском счете сумма ПС и вы ежемесячно дополнительно вносите одну и туже сумму ПЛТ, то функция вычислит сумму на Вашем банковском счете через Кпер месяцев. Теперь несколько замечаний:

1. Предполагается, что капитализация процентов происходит также периодически с процентной ставкой равной величине СТАВКА;
2. Процентная ставка указывается за период (если период равен месяцу, а задана годовая ставка =10%, то СТАВКА =10%/12);
3. По умолчанию аргумент Тип=0, т.е. пополняющие счет вклады делаются в конце каждого периода. Если Тип=1, то пополняющие счет вклады делаются в начале каждого периода;
4. Начальная сумма вклада ПС м.б. =0, но тогда суммы дополнительных взносов ПЛТ не должны быть  =0;
5. Суммы дополнительных взносов м.б. =0, но тогда Начальная сумма вклада ПС не должна быть =0.

Примечание . Английский вариант функции: FV(rate, nper, pmt, [pv], [type]), т.е. Future Value – Будущая Стоимость.

Расчеты в БС() производятся по этой формуле:

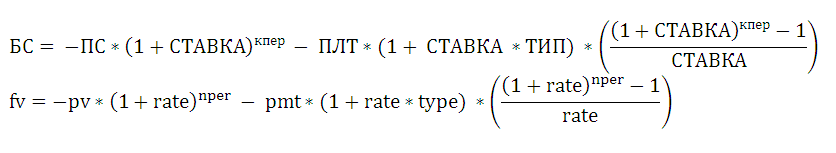
Из формулы видно, будущая стоимость состоит из 2-х составляющих: будущая стоимость инвестиции ПС (вычисляется по формуле сложных процентов ) и будущая стоимость периодических равновеликих взносов ПЛТ (вычисляется по формуле аннуитета ).

Примечание . При БС=0 (начальная инвестиция =0) Будущая стоимость не зависит от параметра Тип.

Вычислим Будущую стоимость в случае накопления вклада. Исходные данные приведены на рисунке ниже.

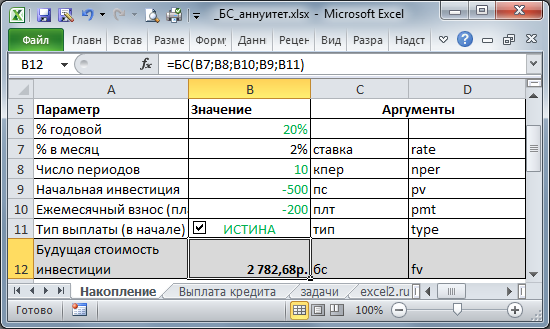
В результате расчетов получим следующий график накопления вклада (см. файл примера Лист Накопление ).

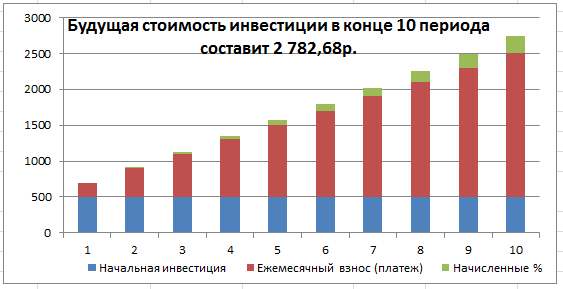
Примечание . Функцию БС() можно также использовать для вычисления баланса на конец периода (см. файл примера Лист Накопление, столбец G ). Для этого используйте выражение = БС(ставка; кпер; плт; [пс]; [тип])/ (1+ставка*тип)

Примечание . При Тип=1 (начисление процентов в начале периода), баланс на конец последнего периода не равен БС (как при Тип=0), т.к. учитывается начисление процентов на следующий день после окончания последнего периода! Т.е. к балансу на конец последнего периода прибавляется величина =БС(ставка; кпер; плт; [пс]; [тип])*ставка

Вывод формулы Будущей стоимости

Формула аннуитета может быть получена как сумма членов геометрической прогрессии, где знаменатель =(1+ставка). Выведем формулу аннуитета при Тип=0 в случае накопления вклада в течение Кпер периодов. Накопление вклада производится регулярными взносами (платежами) ПЛТ, начальная сумма вклада =0 (ПС). За период действует процентная ставка =Ставка. Итак, выводим:

1. Т.к. платеж вносится в конце периода, то в 1-й период проценты не начисляются (банк не использовал взнос). Баланс на конец периода =ПЛТ (взнос также сделан в конце периода).
2. В конце 2-го периода проценты начисляются на величину ПЛТ (на взнос, который был сделан в 1-м периоде). Баланс на конец 2-го периода =ПЛТ+ ПЛТ*ставка+ПЛТ= ПЛТ+ПЛТ*(1+ставка).
3. В конце 3-го периода проценты начисляются на величину ПЛТ+ ПЛТ *(1+ставка), т.е. на баланс начала 3-го периода (или на баланс конца 2-го периода, что естественно, то же самое). Баланс на конец 3-го периода = (ПЛТ+ ПЛТ *(1+ставка))*ставка+ (ПЛТ+ ПЛТ *(1+ставка))+ПЛТ=(ПЛТ+ ПЛТ *(1+ставка))*( 1+ставка) + ПЛТ= ПЛТ *(1+ставка)^2+ ПЛТ *(1+ставка)+ПЛТ.
4. Очевидно, что баланс в конце последнего периода (кпер)= ПЛТ *(1+ставка)^(кпер-1)+ ПЛТ *(1+ставка)^ (кпер -2)+… +ПЛТ *(1+ставка)^2+ ПЛТ *(1+ставка)+ПЛТ. Заметим, что ПЛТ = ПЛТ *(1+ставка)^0
5. Формула, полученная на предыдущем шаге, является суммой членов геометрической прогрессии и одновременно =БС: первый член геометрической прогрессии =ПЛТ, знаменатель =(1+ставка). Т.е. БС=ПЛТ*(1-(1+ставка)^ кпер)/(1-(1+ставка))= ПЛТ*(((1+ставка)^ кпер)-1)/ставка. Полученное уравнение с точностью до знака совпадает со вторым слагаемым формулы для вычисления БС (при Тип=0).

Как показано в файле примера (лист Накопление) при задании аргументов функции БС() у ПЛТ указывают знак минус (в этом случае БС>0). Противоположные знаки у ПЛТ и БС указывают на то, что мы имеем дело с разнонаправленными денежными потоками: БС – это деньги, которые банк вернет нам после окончания вклада, а -ПЛТ – это деньги, которые мы регулярно отдаем банку . Поэтому, окончательная формула для БС() (при ПС=0 и Тип=0): =- ПЛТ*(((1+ставка)^ кпер)-1)/ставка

Использование функции БС() в случае возврата кредита

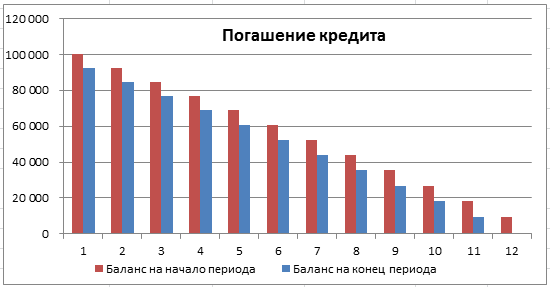
Функция БС() может быть использована также для нахождения остаточной стоимости ссуды по прошествии заданного количества периодов (см. файл примера Лист Выплата кредита ). Для этого используйте формулу =-БС(ставка; кпер; плт; [пс]; [тип])/ (1+ставка*тип)

При выплате кредита обычно предполагается, что по прошествии Кпер периодов (т.е. по истечению срока займа) Будущая стоимость кредита станет равна 0 (т.е. кредит будет полностью возращен).

Примечание : в файле примера приведено решение нескольких простых задач по определению Будущей стоимости.