Подбор параметра в EXCEL

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную - скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра .

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным .

Простейший пример

Найдем значение параметра b в уравнении 2*а+3*b=x , при котором x=21 , параметр а= 3 .

Подготовим исходные данные.

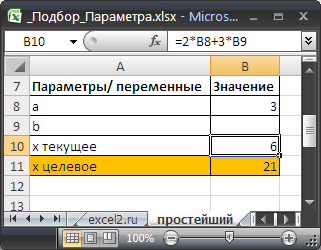
Значения параметров а и b введены в ячейках B8 и B9 . В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x ). Целевое значение x в ячейке B11 введено для информации.

Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …) .

В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b ).

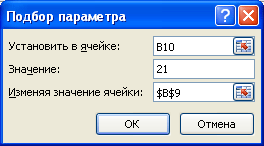
Нажмите ОК.

Инструмент Подбор параметра подобрал значение параметра b равное 5.

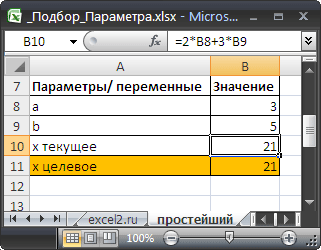
Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно .

Примечание : Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b , которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший .

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X - аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

Калькуляция, подбираем значение прибыли

Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

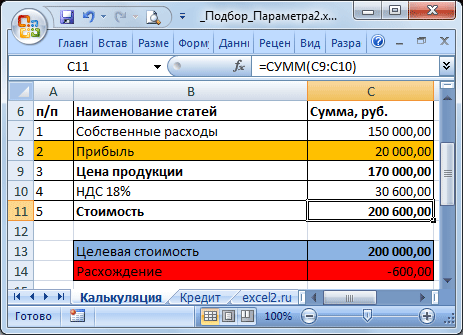
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13 ). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли ( С8 ), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение ( С14 ) равно 0.

В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11 ) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).

Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра .

Выделите ячейку С14 , вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).

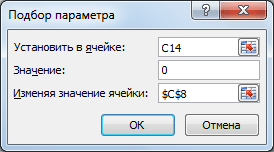
Нажмите ОК.

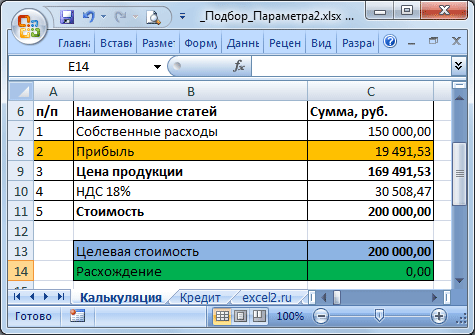
Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.

Подбор суммы кредита

Предположим, что нам необходимо определить максимальную сумму кредита , которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).

В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет ). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.

Введем в ячейку B 6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B 7 , % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).

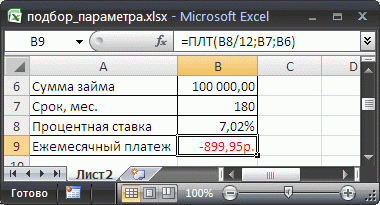
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:

• на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …;
• в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере - это ячейка B9 ;
• введите искомый результат в поле Значение . В данном примере он равен -1800 ;
• В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере - это ячейка B6 ;
• Нажмите ОК

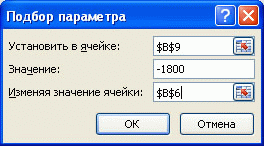
Что же сделал Подбор параметра ? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат - 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.

Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения . Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.

Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.