Аннуитет. Расчет в EXCEL количества периодов

Рассчитаем в MS EXCEL сколько времени потребуется для погашения кредита в случае равных ежемесячных платежей (по аннуитетной схеме). Процентная ставка и величина платежа - известны, начисление процентов за пользование кредитом – ежемесячное. Также в статье разберем случай накопления вклада.

Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат. В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа) показано как рассчитать величину регулярной суммы для погашения кредита или ссуды. Расчет количества периодов, необходимых для погашения кредита произведем сначала с помощью финансовой функции MS EXCEL КПЕР(), затем приведем расчет с помощью эквивалентной формулы (см. файл примера ).

Функция КПЕР(ставка; плт; пс; [бс]; [тип]) позволяет вычислить количество периодов, через которое текущая сумма вклада (пс) станет равной заданной сумме (бс) при известной процентной ставке за период (ставка) и известной величине пополнения вклада (плт). Бс ( будущая стоимость ) может быть =0 или опущена. Тип – это число 0 или 1, обозначающее, когда должна производиться выплата (и соответственно начисление процентов): 0 – в конце периода, 1 – в начале. Также функцию КПЕР() можно использовать для определения количества периодов, необходимых для погашения долга по ссуде.

Примечание . Обзор всех функций аннуитета найдете здесь .

Эквивалентная формула для расчета количества периодов:

Если ставка равна 0, то: Кпер = (Пс + Бс) /ПЛТ

Задача1

Сколько времени потребуется для погашения кредита 1 млн. рублей в случае равных ежемесячных взносов. Начисление процентов за пользование кредитом – ежемесячное, годовая процентная ставка = 10%. Ежемесячный платеж 50 000р.

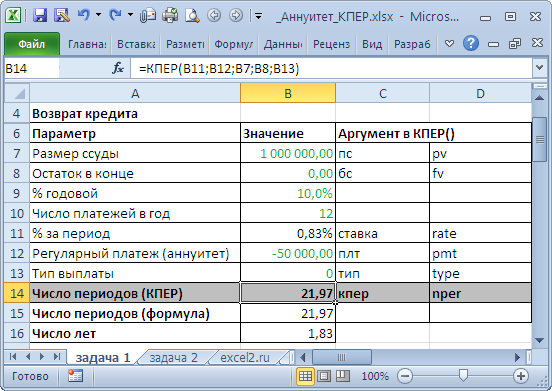
Решение 1 Так как погашение кредита производится ежемесячно (12 раз в году), то ставка за период составит 10%/12. Формула =КПЕР(10%/12;-50000;1000000;0;0) вернет количество периодов, после которых кредит будет возвращен в полном размере. Знак минус перед 2-м аргументом функции (величина ежемесячного платежа) показывает, что разнонаправленные денежные потоки должны иметь разные знаки (+1000000 – это деньги, которые банк дал нам, -50000 – это деньги, которые мы возвращаем банку ). Конечно, можно и наоборот: деньги, которые банк дал нам учитывать со знаком минус, а те деньги, которые мы отдаем банку учитывать со знаком +. Формула вернет 21,97, т.е. потребуется 22 месяца, чтобы полностью вернуть 1 млн. руб., возвращая ежемесячно по 50 тыс. руб. (последний платеж будет несколько меньше, о том, как его рассчитать – читайте ниже).

Расчет последнего платежа При расчете количества периодов погашения ссуды может получиться нецелое количество периодов. В этом случае, последний платеж будет несколько меньше, чем предыдущие. Найдем величину этого платежа. Учтем, что в последнем периоде нам будет необходимо погасить оставшуюся задолженность и заплатить % банку (% от суммы оставшейся задолженности). Найдем сначала количество полных периодов =ЦЕЛОЕ(КПЕР(10%/12;-50000;1000000;0;0)) и поместим результат в ячейку G21. Чтобы вычислить сколько было погашено основной суммы долга за все целые периоды можно использовать формулу =СУММПРОИЗВ(ОСПЛТ(10%/12;СТРОКА(ДВССЫЛ("1:"&G21)); КПЕР(10%/12;-50000;1000000;0;0);1000000;0;0)) (Альтернатива – используйте функцию ОБЩДОХОД() )

Примечание . Сумму платежа, идущую на оплату основной суммы долга в один определенный период, можно вычислить с помощью функции ОСПЛТ() . Складывая результат ОСПЛТ() для всех целых периодов с помощью функции СУММПРОИЗВ() получим сколько было погашено основной суммы долга.

Далее вычтем из суммы кредита выплаченную сумму за все целые периоды (с учетом знаков). Затем вычислим проценты за последний период = СУММПРОИЗВ(…)*10%/12 Сложим остаток основной суммы долга и проценты за последний (неполный) период (см. файл примера ). В результате получим -48487,18р. (это несколько меньше регулярного платежа -50000р.)

Если функция КПЕР() возвращает ошибку В некоторых случаях функция КПЕР() возвращает значение ошибки #ЧИСЛО! Разобраться, почему это происходит, можно, вспомнив альтернативную формулу (см. выше). Понятно, что логарифм числа может быть вычислен только для положительного числа, а это означает, что величина платежа ПЛТ должна быть больше величины ежемесячных процентов начисляемых на остаток тела кредита, т.е. больше ПС*СТАВКА (это справедливо только при БС=0 и ТИП=0). Оно и понятно, нам нужно ежемесячно не только оплачивать проценты, но и возвращать основную сумму долга.

Количество периодов, через которое будет погашено 80% кредита Сколько времени потребуется, чтобы погасить кредит не полностью, а например, на 80%? Записав формулу =КПЕР(10%/12;-50000;1000000;-1000000*(1-80%);0) получим, что для этого потребуется 17,88 периодов (месяцев). Величину БС = -1000000*(1-80%) мы нашли пользуясь тождеством для аннуитета (справедливо, если Тип=0): СУММ(ОСПЛТ(за все периоды)) + ПС + БС = 0 Из условий задачи ПС = 1000000 (начальная сумма кредита), выплаченная сумма кредита, т.е.  СУММ(ОСПЛТ(за все периоды)) равна -1000000*80%. Решая уравнение, получим, что БС = -1000000*(1-80%). БС в данном случае – это непогашенная сумма кредита (конечно, чтобы найти, что БС=20% от суммы кредита, не требует использования тождества. Но важен знак БС).

Задача2

Рассчитать, через сколько времени вклад размером 200 000 руб. достигнет 1 000 000 руб., если годовая процентная ставка по вкладу 10% годовых, начисление процентов производится ежеквартально, также ежеквартально вклад пополняется на 10 000 руб.

Решение2 Так как взносы и начисление процентов происходит ежеквартально (4 раза в год), то ставка за период составит 10%/4. Формула =КПЕР(10%/4;-10000;-200000;1000000;0) вернет количество периодов, после которых вклад достигнет 1 млн. руб., т.е. 34,31 квартал (см. файл примера, лист Задача2 ).