Аннуитет. Определяем процентную ставку в EXCEL

Пусть известна сумма и срок кредита, а также величина регулярного аннуитетного платежа. Рассчитаем в MS EXCEL под какую процентную ставку нужно взять этот кредит, чтобы полностью его погасить за заданный срок. Также в статье разберем случай накопления вклада.

Для расчета процентной ставки в аннуитетной схеме используется функция СТАВКА() .

Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение]) возвращает процентную ставку по аннуитету.

Примечание . Английский вариант функции: RATE(nper, pmt, pv, [fv], [type], [guess]), т.е. Number of Periods – число периодов.

]]> Вот что написано на сайте MS ]]> : Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1 (подробнее см. обзорную статью о функциях аннуитета ).

Если постараться решить это уравнение относительно параметра Ставка, то мы получим степенное уравнение (степень уравнения и, соответственно, число его корней будет зависеть от значения Кпер). В отличие от других параметров ПЛТ, БС, ПС и Кпер, найти универсальное решение этого уравнения для всевозможных степеней невозможно, поэтому приходится использовать метод итераций (по сути, метод подбора ). Чтобы облегчить поиск Ставки методом итераций, используется аргумент Предположение. Предположение - это приблизительное значение Ставки, т.е. прогноз на основании нашего знания о задаче. Если значение предположения опущено, то оно полагается равным 10 процентам. Значение Предположение также полезно в случае , если имеется несколько решений уравнения – в этом случае находится значение Ставки ближайшее к Предположению .

Задача1 – Выплата кредита

Определим под какую годовую ставку мы можем взять 100 000 руб., выплачивая ежемесячно 3000 руб. в течение 5 лет.

Примечание . Аннуитетная схема погашения кредита подробно рассмотрена в статье Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа) .

В условии задачи содержится следующая информация:

• Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
• Проценты начисляются в конце каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0;
• В конце срока задолженность должна быть равна 0 (БС=0).

В результате формула для вычисления годовой ставки будет выглядеть так =12*СТАВКА(12*5;-3000;100000;0;0) или =12*СТАВКА(12*5;-3000;100000) Знак минус у регулярного платежа показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые банк дал нам, -3000 – это деньги, которые мы возвращаем банку . Результат вычисления = 26,10%

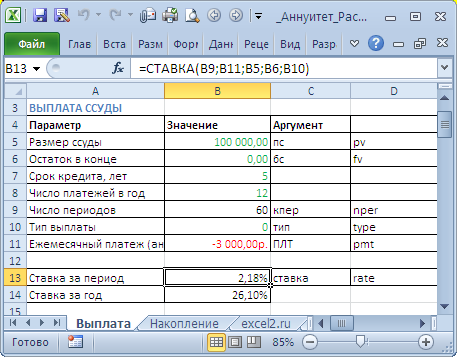
Формула может вернуть отрицательные значения ставки. Это происходит, когда сумма всех регулярных платежей недостаточна для погашения кредита даже при 0 ставке. Но, в нашем случае все в порядке: 60*(3000)=180000>100000. Отрицательная ставка означает, что банк выплачивает нам проценты за пользование кредитом, что является абсурдом. Это, конечно, ошибка (попробуйте например, в файле примера на Листе Выплата установить платеж =-1000).

Если задать платеж = 0 или того же знака, что и сумма кредита, то функция СТАВКА() вернет ошибку #ЧИСЛО! Это и понятно, при нулевых платежах погасить кредит невозможно.

Примечание . С помощью Подбора параметра можно найти величину регулярного платежа, который бы обеспечил выплату кредита при заданной процентной ставке (обратная задача). Но, по большому счету, в этом нет необходимости – для этого существует функция ПЛТ() .

Задача2 – Накопление суммы вклада

Определим, с какой годовой ставкой мы можем накопить 1 000 000 руб., внося ежемесячно по 10 000 руб. в течение 5 лет. (см. файл примера на Лист Накопление )

Примечание . Аннуитетная схема накопления целевой суммы подробно рассмотрена в статье Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад .

Формула для вычисления годовой ставки будет выглядеть так =12*СТАВКА(12*5;-10000;0;1000000) =19,38%

Здесь ПС=0, т.е. начальная сумма вклада =0 ( Приведенная Стоимость ). Целевой вклад = 1000000 (БС – Будущая Стоимость ).

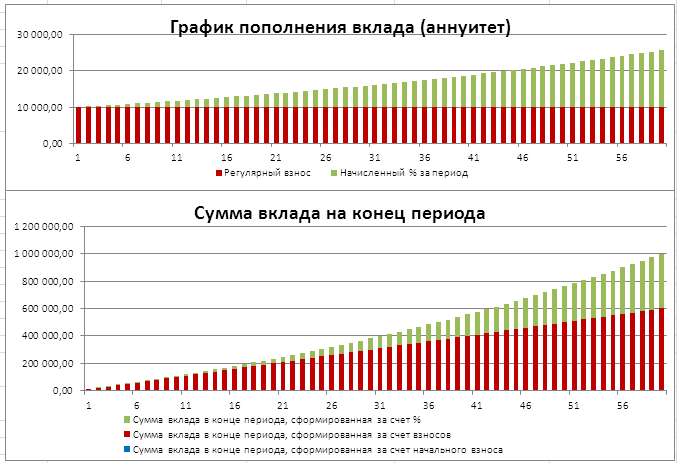
Если суммарное количество взносов будет > целевой стоимости (1000000), то ставка станет отрицательной, чтобы соблюсти наше требование БС=1000000.

Если задать величину пополнения = 0 или того же знака, что и целевая сумма, то функция СТАВКА() вернет ошибку #ЧИСЛО! Это и понятно, при нулевых взносах накопить ничего не получится. Взнос того же знака, что и целевая сумма, вероятно, означает, что банк платит нам. Но, это не возможно, т.к. начальная сумма вклада =0, поэтому выдается ошибка.