Контрольные карты являются инструментом статистического управления процессами (SPC - Statistical Process Control). В статье показано как создать Контрольные карты средних и размахов (виды контрольных карт Шухарта, совместное использование которых рекомендуется).

Примечание: Статья написана для подготовленного читателя, который знаком с разделами Описательная статистика и Статистический вывод. Для таких читателей или для тех, кто предпочитает вспомнить теорию, лежащую в основе контрольных карт, из других источников (например, прочитав ГОСТ Р ИСО 7870 или учебник по статистике), рекомендуется сразу перейти к разделу Построение контрольных карт.

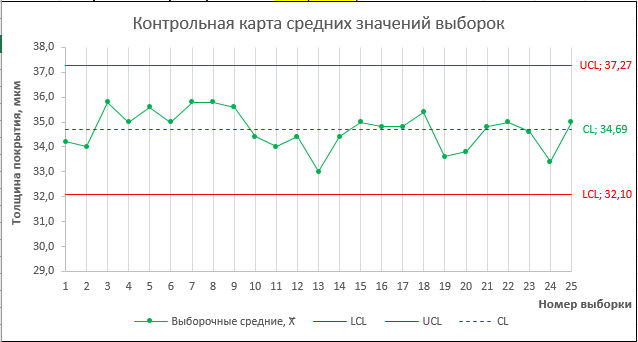
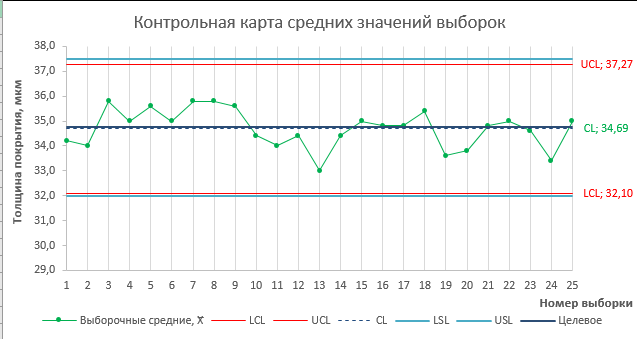
В данной статье мы будем строить Контрольную карту Средних значений и Контрольную карту Размахов. В итоге мы получим вот такой шаблон карты в MS EXCEL:

Немного о модели контрольных карт

В 1920-х годах доктор Уолтер А. Шухарт предложил следующую общую модель контрольных карт:

1) Пусть w это выборочная статистика, которая измеряет некоторую непрерывно изменяющуюся характеристику качества, представляющую интерес (например, толщину покрытия).  

2) Тогда элементы контрольной карты, а именно Центральная линия CL (Center Line), Верхняя контрольная граница UCL (Upper Control Limit) и Нижняя контрольная граница LCL (Lower Control Limit) определяются следующим образом:

CL = μ_w

UCL = μ_w + k * σ_w

LCL = μ_w - k * σ_w

где k - расстояние контрольных пределов от центральной линии, выраженное в единицах стандартного отклонения σ_w. Исторически сложилось так, что k=3 стало общепринятым стандартом в промышленности.

Примечание: Ниже предполагается, что w рассчитывается на основании выборки размера n. Данная статистика, как любая случайная величина, имеет некую функцию распределения со средним значением (обозначим μ_w)  и со стандартным отклонением σ_w. Пусть всего выборок будет m, т.е. для построения карты нам потребуется m*n измерений.

Теперь рассмотрим частный случай - построение Контрольной карты Средних значений. В этом случае выборочная статистика w, как очевидно из названия карты, будет являться средним значением выборки (будем обозначать это среднее как величину х̄ ). Именно эти выборочные средние мы будем отображать на контрольной карте данного типа (всего значений х̄  будет m). Чтобы не путаться также μ_w обозначим как μ_х̄ , а σ_w как σ_х̄.

CL =μ_х̄

UCL = μ_х̄ + k * σ_х̄

LCL = μ_х̄ - k * σ_х̄

Примечание: В файле примера σ_х̄. указана как σ_x-bar, чтобы можно было указать эту величину в ячейке EXCEL без лишних манипуляций.

Теперь определим элементы контрольных карт именно для нашей Контрольной карты Средних значений:

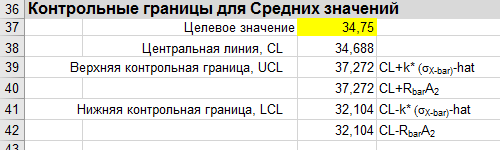
1) Центральная линия CL - это среднее значение процесса μ_х̄ , которое, как правило, неизвестно. Для нашей карты мы заменим его средним значением всех х̄  (обозначим х̄̄ ), которое является несмещенной оценкой истинного значения μ_х̄ .

2) Как видно из формул выше, для определения контрольных границ UCL и LCL необходимо знать стандартное отклонение σ_х̄, которое в общем случае не известно. Здесь, как и для μ_х̄, мы можем его заменить оценкой, полученной на основании имеющихся выборок. Оценку можно сделать с использованием среднего значения стандартных отклонений выборок s_i (это среднее значение обычно обозначают как s̄ ). Если выборки содержат 10 или менее значений, то вместо s̄ допускается использовать средний размах выборок (обозначим как R̄). В этой статье для определения контрольных границ UCL и LCL будем использовать именно размах (размах каждой выборки будем вычислять как разность максимального и минимального значения выборки). Далее покажем как оценить σ_х̄  через средний размах R̄.

Оцениваем неизвестные параметры распределений

Как было сказано выше, оценку стандартного отклонения σ_х̄  выполним через средний размах выборок R̄. Но, перед тем как двинуться дальше давайте уточним как мы получаем исходные данные, на основании которых будем строить контрольные карты.

Предположим для конкретики что у нас есть производственный процесс по нанесению покрытий. Мы хотим ответить на вопрос является ли наш процесс стабильным или нет. Для этого мы решили провести эксперимент по измерению толщины некого покрытия. Обозначим толщину как величину Х. Измерив n значений Х в некий момент времени, мы объединим их в выборку и вычислим х̄_i, также вычислим размах R_i. Понятно, что измеренные значения величины Х в выборке будут отличаться друг от друга, т.к. обычно процесс подвержен влиянию случайных причин (колебания температуры внешней среды, небольшие скачки напряжения в электросети, неоднородность материала, который используется для нанесения покрытия и пр.). Все эти непредсказуемые, неконтролируемые причины придают величине Х случайный характер. Продолжая измерения через определенные промежутки времени мы получим всего m значений х̄ и столько же размахов. Далее вычислим х̄̄ - среднее всех х̄  -  это нужная нам для построения Центральной линии оценка величины μ_х̄ .

Примечание: Построение эксперимента является отдельной задачей в статистике и в данной статье не рассматривается. При планировании эксперимента определяется размер выборки n, периодичность и условия измерений и много другое. Корректность эксперимента по получению данных определяет корректность сделанных статистических выводов.

Поскольку Х является случайной величиной, то она может быть описана функцией распределения с параметрами μ (среднее, т.е. наиболее типичное значение Х) и σ (стандартное отклонение, характеризующее разброс около среднего). Выборочное среднее (х̄), как было сказано выше, также является случайной величиной со своей функцией распределения (не обязательно совпадает с функцией распределения величины Х) с параметрами μ_х̄  и σ_х̄. Воспользовавшись Центральной предельной теоремой мы можем получить формулу для вычисления выборочного стандартного отклонения σ_х̄ =σ/√n. Однако, σ, точнее ее оценка, нам пока не известна. Оценку σ обозначим как σ-hat, т.е. "сигма с крышкой" или .

Теперь вспоминаем, что оценку стандартного отклонения можно сделать через средний размах R̄. Из теории известно, что существует статистическая зависимость между средним размахом R̄ для данных из нормального распределения и стандартным отклонением этого распределения. Вот эта зависимость: R̄ = d₂ * σ-hat или σ-hat = R̄ / d₂. Это соотношение зависит только от размера выборки n. Коэффициент d₂ для различных размеров выборки n затабулирован, в частности эти значения можно также найти в файле примера или, например, в ГОСТ Р ИСО 7870-2-2015. Следовательно, оценка для σ_х̄  может быть вычислена как R̄ / (d₂*√n). Таким образом, формулы для вычисления границ UCL и LCL Контрольной карты Средних значений следующие:

UCL = х̄̄  + 3 * R̄ / (d₂*√n)

LCL = х̄̄  - 3 * R̄ / (d₂*√n)

Фактически мы строим контрольную карту не для характеристики качества Х, а для выборочных средних х̄ .

Примечание: нужно обратить внимание, что при получении оценки σ через R̄ мы использовали предположение, что величина Х имеет нормальную функцию распределения. А, действительно ли это так? Это один из вопросов, на который нужно получить ответ при планировании эксперимента в каждом конкретном случае.

Теперь займемся вычислением границ и центральной линии Контрольной карты Размахов. Правда, возникает один логичный вопрос: А зачем ее строят дополнительно с Контрольной картой средних значений?

Дело в том, что вычислив границы UCL и LCL мы неявно предположили, что расстояние между границами UCL и LCL "стабильно" в ходе всего эксперимента. Но, ведь мы их сделали на основе точечных (усредненных по всем выборкам) оценок. Кстати, под словом "стабильный" процесс будем понимать такой процесс, при котором наблюдаемые отклонения в значительной степени находятся в пределах контрольных границ. Если посмотреть на формулы UCL и LCL, то их стабильность означает стабильность размахов выборок, т.е. R_i. Оценить эту стабильность можно с использованием контрольной карты, аналогичной той, что мы строили выше. В этом случае выборочная статистика w будет величиной размаха R, которая является случайной величиной со своим распределением, описываемым собственным средним значением μ_R и стандартным отклонением σ_R. Эти два параметра распределения также можно оценить. μ_R оценивают как R̄. Для оценки σ_R, не вдаваясь в подробности, используют выражение d₃*(R̄/d₂). Коэффициент d₃ для различных размеров выборки n затабулирован, как и d₂.

Как мы делали выше - определим элементы контрольных карт именно для нашей Контрольной карты Размахов:

1) Центральная линия CL - это среднее значение всех размахов, т.е. R̄.

2)

UCL = R̄ + 3 * d₃*(R̄/d₂) = R̄ * (1 + 3 * d₃/d₂) = R̄ * D₄

LCL = R̄ - 3 * d₃*(R̄/d₂) = R̄ * (1 - 3 * d₃/d₂) = R̄ * D3

Как легко догадаться, коэффициенты D₃ и D₄ для различных размеров выборки n затабулированы. 

Наконец, мы получили расчетные формулы для всех элементов обоих контрольных карт. Можно приступать к построению.

Построение контрольных карт

Сначала подготовим место для таблицы со значениями выборки (значения измерений толщины Х).

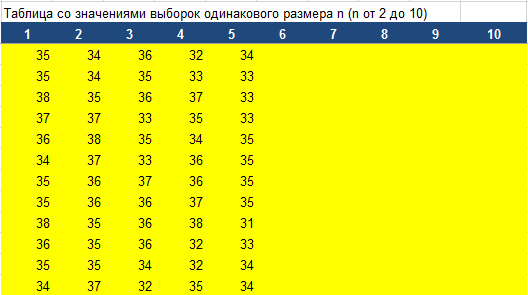
Размер выборки в нашем случае не должен превышать 10, поскольку мы оценивали стандартное отклонение случайной переменной Х через размах (см. выше).

Количество выборок для построения контрольной карты (определения границ) может быть разным, однако будем придерживаться рекомендаций Шухарта - возьмем 25 выборок.

Примечание: для обучающих целей значения выборки из нормального распределения можно сгенерировать с помощью формулы =ЦЕЛОЕ(НОРМ.ОБР(СЛЧИС();$C$37;$C$37/17)). Формула находится в ячейке P54. В ячейке C37 содержится некое целевое значение. Стандартное отклонение выражено в 1/17 от целевого значения (чтобы диапазон 6 сигма составлял примерно 35% от целевого). Про генерацию случайных величин можно почитать здесь.

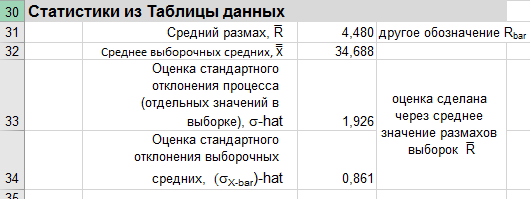
Теперь на основании значений выборок вычислим необходимые статистики - оценки параметров распределений.

Все вычисления делаются с помощью довольно простых формул:

• Размахи каждой выборки R_i =МАКС(E55:M55)-МИН(E55:M55)
• Выборочные средние х̄  =СРЗНАЧ(E55:N55)
• Средний размох R̄ =СРЗНАЧ(C55:C79)
• Среднее значение всех х̄  (т.е. х̄̄ ) =СРЗНАЧ(B55:B79)
• Оценка стандартного отклонения процесса (отдельных значений в выборке), σ-hat =C31/ВПР(C50;P31:R39;2;ИСТИНА) - здесь мы просто извлекаем из таблицы значение d₂, соответствующего n
• Оценка стандартного отклонения выборочных средних (оценка величины σ_х̄ ) =C33/КОРЕНЬ(C50)

Контрольные границы вычисляются также по простейшим формулам:

Далее строим контрольные карты с помощью Точечной диаграммы с несколькими рядами данных.

СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .

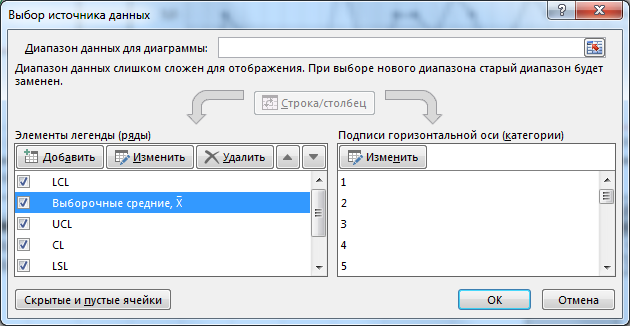
Если заданы границы спецификации, то можно их также отобразить на диаграмме.

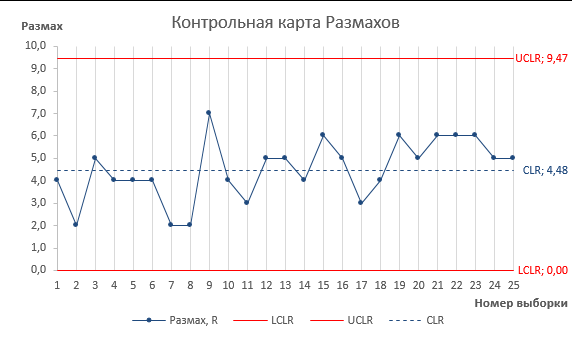
Аналогичным образом строится и Контрольная карта размахов.

Как видно из контрольных карт - процесс стабилен. Все выборочные средние и размахи хорошо укладываются в контрольные границы (+/- 3 стандартных отклонения).