Прогнозирование методом скользящего среднего в MS EXCEL
4 августа 2021 г.
- Группы статей
Сам метод скользящего среднего рассмотрен в статье Скользящее среднее в MS EXCEL, в которой показано как для этого использовать инструмент MS EXCEL Пакет анализа, а также линию тренда и формулы.
В этой статье рассмотрим не сам метод сглаживания, а его применение для прогнозирования. Как было сказано во вводной статье про прогнозирование, метод прогнозирования подбирается в соответствии с процессом, который генерирует значения временного ряда. Поэтому в файле примера используется как стационарные процессы, будем называть их постоянными, т.к. у них среднее и дисперсия постоянные (хотя фактически это белый шум со смещенным средним), и растущий тренд. Для оценки точности прогнозирования рассчитываются ошибки модели, строится интервал прогнозирования (на самом деле не интервал прогнозирования, а некий доверительный интервал на основе вычисленной ошибки). Так же оценивается адекватность модели.
Примечание: Конечно, прогнозировать процессы типа белого шума, бесперспективное занятие, но, во-первых в файле примера демонстрируются характеристики этого процесса (строится диаграмма рассеяния, функция автокорреляции, диаграмма разброса ошибок и пр.), а во-вторых таблицу с исходными значениями можно заменить и все характеристики будут пересчитаны в файле примера автоматически.
Построение исходного и сглаженного ряда
Для построения рядов можно использовать диаграмму типа График или Точечная. Выберем последний тип – Точечная (ниже будет пояснено почему Точечная в данном случае удобнее).
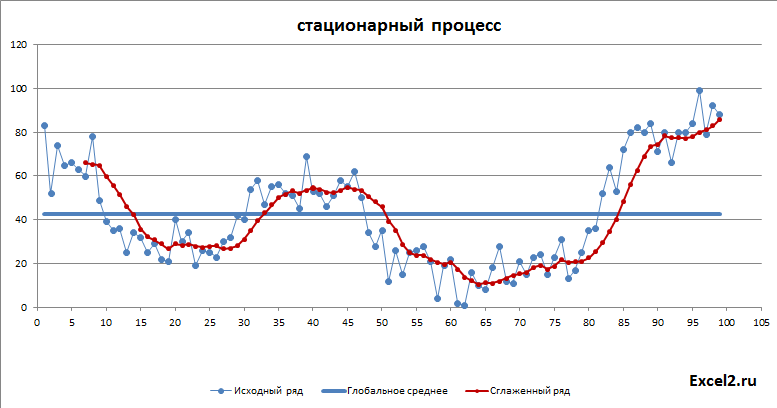
Для исходных рядов нам понадобится 4 столбца с данными (2 «постоянных» процесса, ряд с цикличностью и тренд). В файле примера на листе Исходный и сглаженный ряд это столбцы T:W.
Один из исходных рядов – динамический (столбец U, назовем его «постоянный» процесс с изменениями), т.е. его значения пересчитываются при любом изменении данных листа или после нажатии клавиши F9. Это сделано с помощью формулы =СЛУЧМЕЖДУ($T$10-2*$T$9;$T$10+2*$T$9)
За среднее значение этого ряда взято среднее значение ряда из столбца T =СРЗНАЧ(T13:T111), а диапазон изменения – 2 стандартных отклонения того же ряда =СТАНДОТКЛОН.В(T13:T112).
Такой автоматически генерирующийся ряд удобен для оценки модели – можно получить целый набор прогнозных значений, ошибок и доверительных интервалов. Фактически, конечно, функция СЛУЧМЕЖДУ() генерирует белый шум (с заданным смещением среднего относительно 0).
Примечание: Про функцию СЛУЧМЕЖДУ() можно почитать здесь. Эта функция генерирует непрерывное равномерное распределение, чтобы сгенерировать выборку из нормального или любого другого распределения см. эту статью.
Выбор нужно типа процесса организован с помощью группы переключателей, которая связана с ячейкой I11.

Значения выбранного исходного ряда подставляются в столбце В с помощью формулы =СМЕЩ(T13;;$I$11-1). Подробнее про функцию СМЕЩ() см. здесь.
Сглаженный ряд разместим рядом в столбце С, этот ряд будет формироваться для заданного периода усреднения (ячейка A7) с помощью формулы =ЕСЛИ(A13<$A$7;НД();СРЗНАЧ(СМЕЩ(B13;-$A$7+1;;$A$7)))
Примечание: Про построение сглаженного ряда см. Скользящее среднее в MS EXCEL.
Период усреднения для удобства задается с помощью элемента управления счетчик.
Осталось сформировать данные для линии среднего значений исходного ряда. Для этого понадобится только 2 точки (см. диапазон F43:G44).
Теперь все готово для построения диаграммы.
Примечание: для тех, кто не имеет большого опыта в построении диаграмм MS EXCEL предлагается прочитать эту статью.
Для тренда сглаженный ряд будет выглядеть так: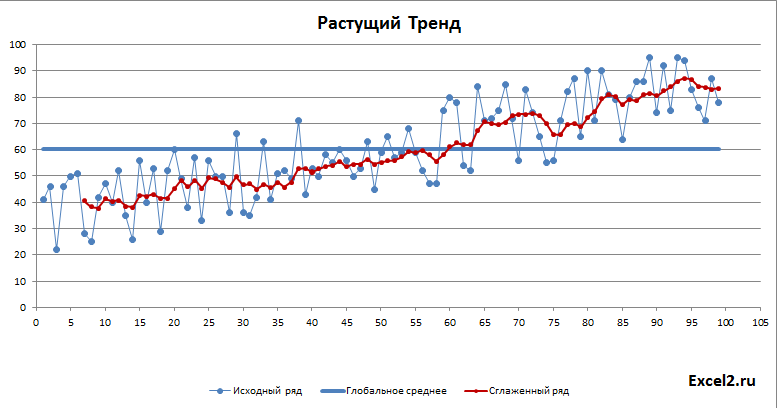
Расчет прогнозного значения
Напомним, что метод скользящего среднего состоит в вычислении средних значений на основе предшествующих значений исследуемого числового ряда. Пусть последнее значение ряда произошло в момент i.
В случае усреднения за 3 периода скользящее среднее в момент i равно:
Yскол.i=(Yi+ Yi-1+ Yi-2)/3
Именно так считает инструмент Пакета Анализа «Скользящее среднее». Понятно, что нас интересует прогноз в будущий момент времени i+1. Положим, что прогнозное значение ряда в момент i+1 равно Yпрогнозн.i+1= Yскол.i
В итоге получаем эквивалентную формулу
Yпрогнозн.i+1=(Yi+ Yi-1+ Yi-2)/3
Для наглядности прогнозное значение на диаграмме изобразим в виде горизонтальной линии зеленого цвета (длина линии ничего не значит). Для этого понадобится только 2 точки (см. диапазон F8:G9).
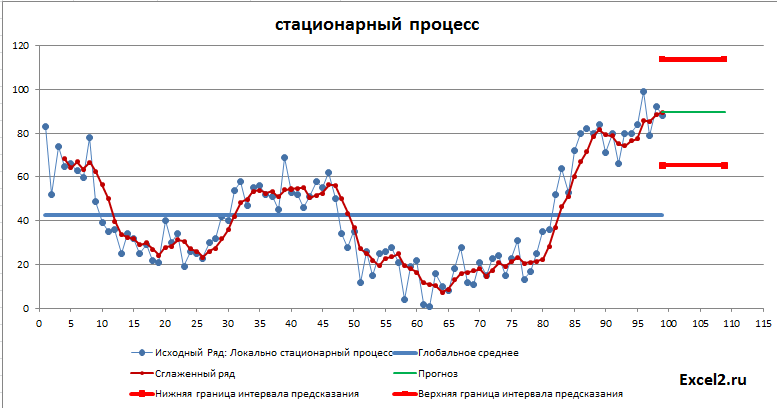
Хотя использование метода скользящего среднего для прогнозирования носит скорее академический, нежели практический интерес, все же покажем как построить что-то типа «интервала предсказания». Для построения интервала воспользуемся ошибкой, которая вычисляется в надстройке Пакет анализа по формуле:
=КОРЕНЬ(СУММКВРАЗН(ИР;СР)/m)
Где m – количество периодов усреднения
ИР - m последних значений Исходного Ряда (ИР)
СР - m последних значений Сглаженного Ряда (СР)
Т.е. данная стандартная ошибка вычисляется по формуле: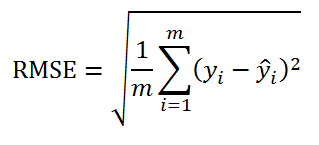
RMSE – это Root Mean Squared Error (среднеквадратическая ошибка).
В файле примера на листе «Прогнозное значение» эта ошибка вычислена по формуле
=КОРЕНЬ(СУММКВРАЗН(СМЕЩ($B$112;-A7;;A7);СМЕЩ($C$112;-A7;;A7))/$A$7)
A7 содержит количество периодов усреднения
СМЕЩ($B$112;-A7;;A7) – это ссылка на диапазон исходного ряда (последние m значений)
СМЕЩ($C$112;-A7;;A7) – это ссылка на диапазон сглаженного ряда
СУММКВРАЗН() вычисляет сумму квадратов разностей
Если вычислить ошибки прогнозирования в отдельном столбце D, то формула для RMSE упростится:
=КОРЕНЬ(СУММКВ(СМЕЩ($D$112;-A7;;A7))/$A$7)
Границы интервала (для заданного уровня значимости альфа) вычисляются как:
Верхняя граница = Yпрогнозн.i+1 + RMSE*tm-1,1-альфа/2
Нижняя граница = Yпрогнозн.i+1 - RMSE*tm-1,1-альфа/2
tm-1,1-альфа/2 - верхний α/2-квантиль распределения Стьюдента с m-1 степенью свободы (это просто число, которое показывает сколько ошибок RMSE нужно, чтобы «интервал предсказания» накрыл прогнозное значение с вероятностью 1-альфа).
Примечание: «Интервал предсказания» вычислен лишь по аналогии с построением доверительного интервала для оценки среднего, для которого у нас была статистическая модель. Для случая скользящего среднего корректность такого построения обосновывается отдельно. В данной статье «Интервал предсказания» построен лишь с целью демонстрации самого процесса построения интервалов предсказания.
Верхний α/2-квантиль вычислим по формуле =СТЬЮДЕНТ.ОБР.2Х(C8;A7-1)
в ячейке С8 находится альфа – уровень значимости (обычно 5%).
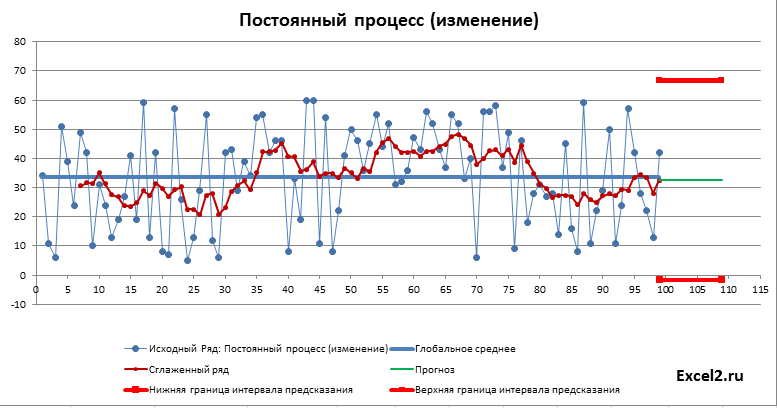
Как видно из диаграммы выше для нашего стационарного процесса (фактически белый шум) прогнозное значение ожидаемо находится около глобального среднего, а доверительный интервал охватывает весь диапазон изменений исходного ряда, т.е. будущее значение этого ряда может появиться на всем интервале, что фактически говорит нам о невозможности предсказания.
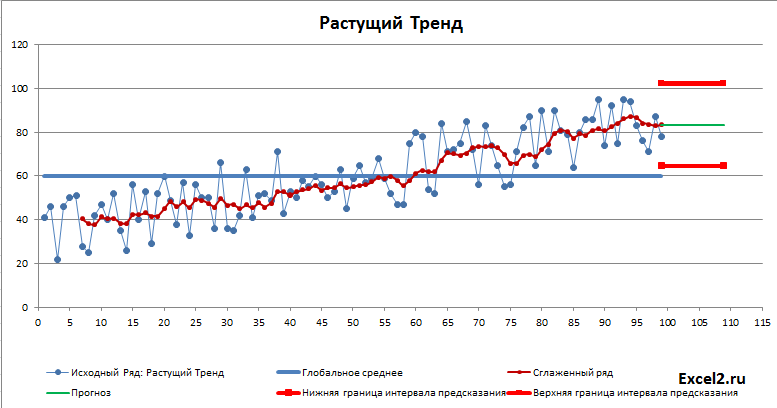
Как и следовало ожидать, для растущего тренда картинка существенно отличается: доверительный интервал уже в 2 раза меньше и прогнозное значение находится вдали от глобального среднего.
Автокорреляция исходного ряда
Исследуем исходный ряд на наличие автокорреляции. Подробно об автокорреляции см. отдельную статью.
Автокорреляция (Autocorrelation, Lagged correlation, Serial correlation) – корреляция значений временного ряда с собственными значениями, сдвинутыми по времени на один или несколько периодов (лагов). Ниже показана диаграмма содержащая исходный ряд и ряд сдвинутый на лаг k=4 (общее количество значений ряда N уменьшится на k, глобальное среднее на диаграмме оставлено как у исходного ряда).
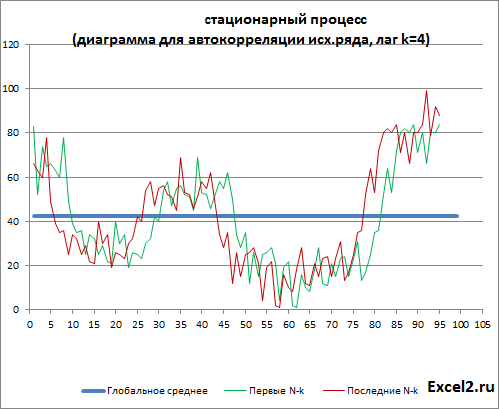
Примечание: Диаграмма построена на листе «Автокорреляция ИР» в файле примера. ИР – Исходный Ряд.
Для оценки автокорреляции используют 3 основных инструмента: график временного ряда (Time Series Plot), диаграмму рассеивания (Lagged Scatterplot) в зависимости от лага и функцию автокорреляции (Autocorelation Function, ACF).
Диаграмма рассеяния используется для отображения возможной взаимосвязи между двумя переменными.
В нашем случае будем исследовать корреляционную зависимость между двумя рядами данных, сдвинутых на лаг k относительно друг друга (см. диаграмму выше).
Для лага k=4 диаграмма рассеяния, очевидно, демонстрирует наличие линейной положительной корреляции.
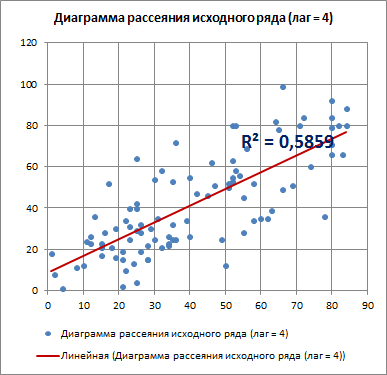
С помощью инструмента диаграммы «Линия тренда» построена линия регрессии и вычислим коэффициент детерминации R2. Ниже мы вычислим R2 с помощью формул, т.к. это просто квадрат коэффициента автокорреляции.
Примечание: Линия тренда подробно описана в разделе Построение линии регрессии статьи про Простую линейную регрессию.
Вычислим коэффициенты автокорреляции для лагов от 1 до 15.
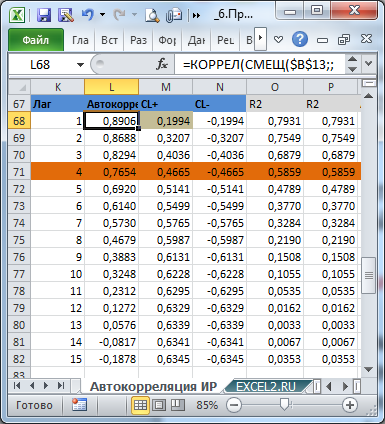
=КОРРЕЛ(СМЕЩ($B$13;;;$B$10-K68);СМЕЩ($B$13;K68;;$B$10-K68))
Два массива в аргументах функции КОРРЕЛ() – это просто 2 ряда, которые сдвинуты на лаг k (ячейка K68) относительно друг друга:
СМЕЩ($B$13;;;$B$10-K68)
СМЕЩ($B$13;K68;;$B$10-K68)
Зависимость коэффициента автокорреляции от лага – это функция автокорреляции (ACF). График ACF – это коррелограмма. Для стационарного процесса (у нас это «постоянный» процесс, фактически белый шум) коррелограмма имеет следующий вид:
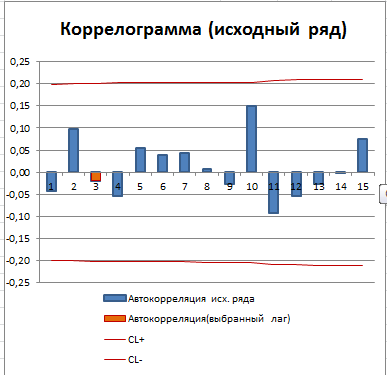
Для другого стационарного процесса (с апериодической цикличностью) коррелограмма имеет совершенно другой вид:
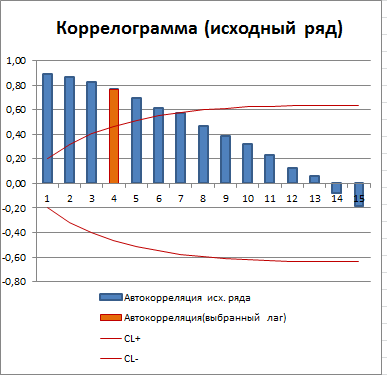
Все коэффициенты автокорреляции, которые выше границ доверительного интервала, являются статистически значимыми (про расчет доверительного интервала для ACF см. статью про Автокорреляцию). Диаграмма рассеяния для выбранного лага (столбец гистограммы, который выделен цветом) также подтверждает отсутствие автокорреляции.
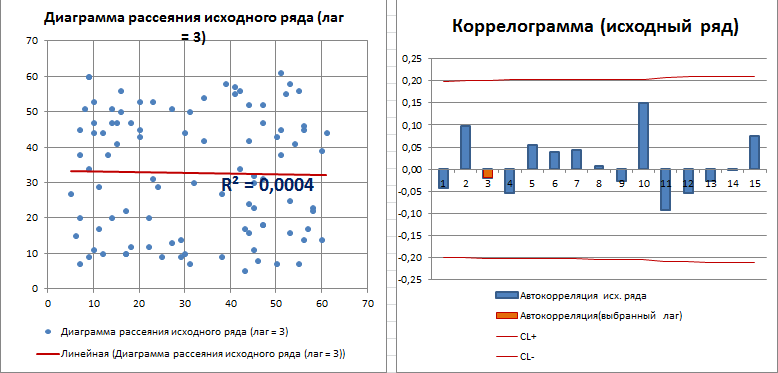
Коэффициент детерминации R2, указанный на диаграмме рассеяния можно рассчитать возведя в квадрат коэффициент корреляции или применив формулу
=КВПИРСОН(СМЕЩ($B$13;;;$B$10-K68);СМЕЩ($B$13;K68;;$B$10-K68))
для тех же массивов, полученных из исходного ряда.
Вычисление ошибок модели
Для прогнозирования значения временного ряда мы использовали модель скользящего среднего с определенным периодом усреднения m. Какое значение является лучшим для прогнозирования?
Критерием оптимальности m является минимизация ошибки модели.
Существует целый ряд формул для вычисления ошибок, но самой лучшей ошибкой для оценки точности модели является среднеквадратичная ошибка (RMSE), вычисленная нами ранее.
Кроме применяются еще несколько других ошибок:
• MAE (Mean Absolute Error, Средняя Абсолютная ошибка). В EXCEL вычисляется по формуле =СРЗНАЧ(ABS(СМЕЩ($D$112;-D10;;D10))). Сначала диапазон ошибок СМЕЩ($D$112;-D10;;D10) в столбце D берется по модулю, затем находится среднее значение. Эта ошибка менее чувствительна к одиночным выбросам, т.к. значения ошибок не возводятся в квадрат.
• MAPE (Mean Absolute Percentage Error, Средняя Абсолютная Процентная Ошибка). В EXCEL вычисляется по формуле =СРЗНАЧ(ABS(СМЕЩ($D$112;-D10;;D10)/СМЕЩ($B$112;-D10;;D10))) Вычисляется практически аналогично MAE, но вместо просто ошибки берется по модулю ее отношение к значению исходного ряда. Получается безразмерная величина. Подходит для исходных рядов с трендом или ярко выраженной сезонностью.
• ME (Mean Error, Средняя ошибка). Эта ошибка показывает имеет ли прогноз смещение. МЕ должна быть около 0. =СРЗНАЧ(СМЕЩ($D$112;-D10;;D10)). ME может быть положительной и отрицательной.
• MPE (Mean Percentage Error, Средняя Процентная ошибка). Вычисляется практически аналогично ME, но вместо просто ошибки берется ее отношение к значению исходного ряда. MPE может быть положительной и отрицательной. =СРЗНАЧ((СМЕЩ($D$112;-D10;;D10)/СМЕЩ($B$112;-D10;;D10)))
Все ошибки вычислены в файле примера на листе Ошибки модели в диапазоне M7:Q11.
Как было сказано выше, для построения «интервала предсказания» прогнозного значения использовалась среднеквадратичная ошибка (RMSE) причем вычисленная не для всего ряда, а лишь на периоде усреднения. Это соответствует формулам MS EXCEL в Пакете анализа. На обоих горизонтах расчета RMSE дает близкие значения, причем в зависимости от лага или значений ряда RMSE вычисленная на периоде усреднения m может давать непредсказуемо либо меньшее либо большее значение по сравнению с RMSE вычисленной для всего ряда (в этом можно убедиться проанализировав RMSE для динамически изменяемого постоянного процесса).
Проверка адекватности модели
На листе Ошибки модели построена диаграмма разброса ошибок и гистограмма ошибок. Эти диаграммы автоматически перестраиваются в зависимости от выбранного лага или типа исходного ряда.
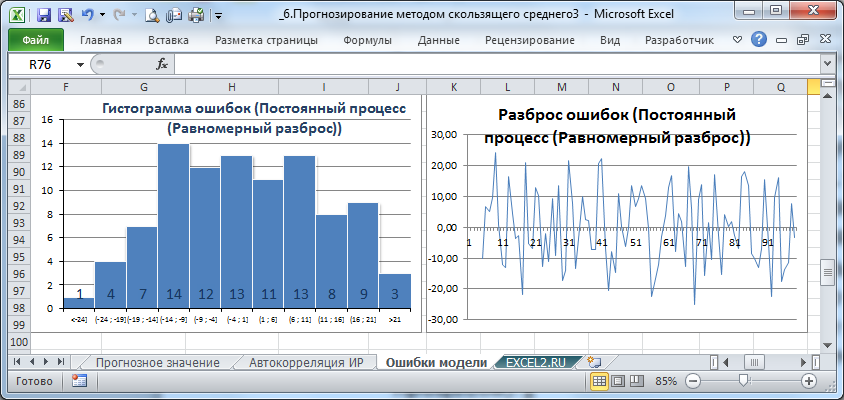
Диаграмму разброса ошибок можно построить на основе диаграммы MS EXCEL типа График. Специальных знаний построения диаграмм практически не требуется. Впрочем, как и для построения Гистограммы. Несколько сложнее построить таблицу исходных данных для гистограммы. Об этом подробно рассказано в статье Гистограмма распределения
Диаграмма разброса ошибок должна демонстрировать колебания ошибок около 0, а гистограмма - типичную выборку из нормального распределения. Проверить распределение ошибок на нормальность можно построить соответствующий график.
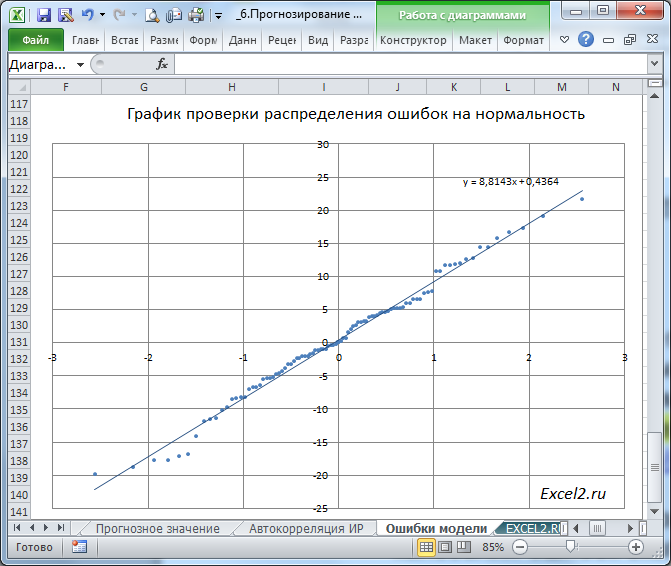
Подробнее о проверке распределения на нормальность см. в этой статье.
В заключение, по аналогии с проверкой исходного ряда на автокорреляцию можно вычислить автокорреляцию ошибок и построить диаграммы рассеяния и коррелограмм.
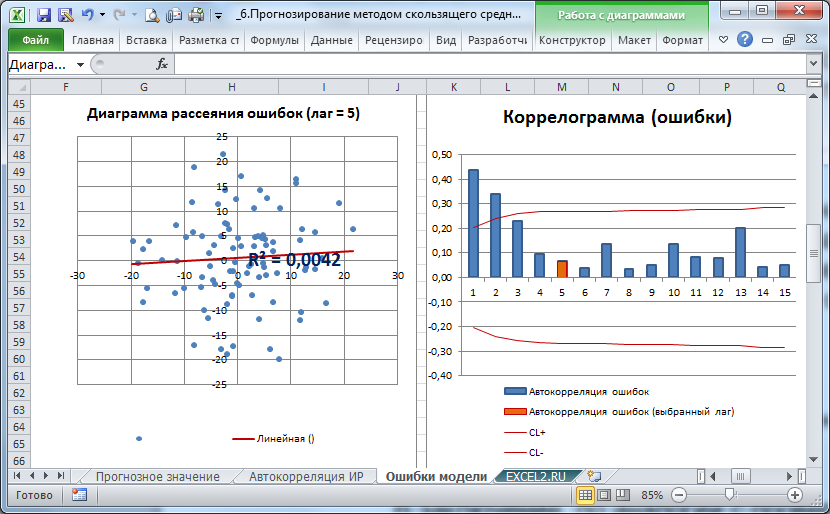
На картинке выше приведены диаграмма рассеяния и коррелограмм для ошибок «постоянного» процесса.
Примечание: На листе «скользящее среднее» объединены все диаграммы, о которых рассказывалось выше в статье.
Комментарии