В первом разделе статьи модели для прогнозирования временных рядов сравниваются с моделями, построение которых основано на причинно-следственных закономерностях.

Во втором разделе приведен краткий обзор трендов временных рядов (линейный и сезонный тренд, стационарный процесс). Для каждого тренда предложена модель для прогнозирования.
Затем даны ссылки на сайты по теории прогнозирования временных рядов и содержащие базы статистических данных.

Disclaimer:
Напоминаем, что задача сайта excel2.ru (раздел Временные ряды ) продемонстрировать использование MS EXCEL для решения задач, связанных с прогнозированием временных рядов. Поэтому, статистические термины и определения приводятся лишь для логики изложения и демонстрации идей. Сайт не претендует на математическую строгость изложения статистики. Однако в наших статьях:
•    ПОЛНОСТЬЮ описан встроенный в EXCEL инструментарий по анализу временных рядов (в составе надстройки Пакет анализа , различных типов Диаграмм ( гистограмма , линия тренда ) и формул);
•    созданы файлы примера для построения соответствующих графиков, прогнозов и их интервалов предсказания, вычисления ошибок, генерации рядов (с трендами и сезонностью ) и пр.

Модели временных рядов и модели предметной области

Напомним, что временным рядом (англ. Time Series) называют совокупность наблюдений изучаемой величины, упорядоченную по времени. Наблюдения производятся через одинаковые периоды времени. Другой информацией, кроме наблюдений, исследователь не обладает.

Основной целью исследования временного ряда является его прогнозирование – предсказание будущих значений изучаемой величины. Прогнозирование основывается только на анализе значений ряда в предыдущие периоды, точнее - на идентификации трендов ряда. Затем, после определения трендов, производится моделирование этих трендов и, наконец, с помощью этих моделей - экстраполяция на будущие периоды.

Таким образом, прогнозирование основывается на фактических данных (значениях временного ряда) и модели ( скользящее среднее , экспоненциальное сглаживание , двойное и тройное экспоненциальное сглаживание и др.).

Примечание : Прогнозирование методом Скользящее среднее в MS EXCEL подробно рассмотрено в одноименной статье .

В отличие от методов временных рядов, где зависимости ищутся внутри самого процесса , в «моделях предметной области» (англ. «Causal Models») кроме самих данных используют еще и законы предметной области.

Примером построения «моделей предметной области» ( моделей строящихся на основе причинно-следственных закономерностей, априорно известных независимо от имеющихся данных ) может быть промышленный процесс изготовления защитной ткани. Пусть в таком процессе известно, что прочность материала ткани зависит от температуры в реакторе, в котором производится процесс полимеризации (температура - контролируемый фактор). Однако, прочность материала является все же случайной величиной, т.к. зависит помимо температуры также и от множества других факторов (качества исходного сырья, температуры окружающей среды, номера смены, умений аппаратчика реактора и пр.). Эти другие факторы в процессе производства стараются держать постоянными (сырье проходит входной контроль и его поставщик не меняется; в помещении, где стоит реактор, поддерживается постоянная температура в течение всего года; аппаратчики проходят обучение и регулярно проводится переаттестация). Задачей статистических методов в этом случае – предсказать значение случайной величины (прочности) при заданном значении изменяемого фактора (температуры).

Обычно для описания таких процессов (зависимость случайной величины от управляемого фактора) являются предметом изучения в разделе статистики « Регрессионный анализ », т.к. есть основания сделать гипотезу о существовании причинно-следственной связи между управляемым фактором и прогнозируемой величиной.

Модели, строящиеся на основе причинно-следственных закономерностей, упомянуты в этой статье для того чтобы акцентировать, что их изучение предшествует теме «временные ряды». Так, часть методов, например «Регрессионный анализ» (используется метод наименьших квадратов - МНК ), используется при анализе временных рядов, но изучаются в моделях предметной области, поэтому неподготовленным «пытливым умам» не стоит игнорировать раздел статистики « Статистический вывод », в котором проверяются гипотезы о равенстве среднего значения и строятся доверительные интервалы для оценки среднего , и упомянутый выше «Регрессионный анализ».

Кратко о типах процессов и моделях для их прогнозирования

Выбор подходящей модели прогнозирования делается с учетом типа моделируемого процесса (наличие трендов). Рассмотрим основные типы процессов.

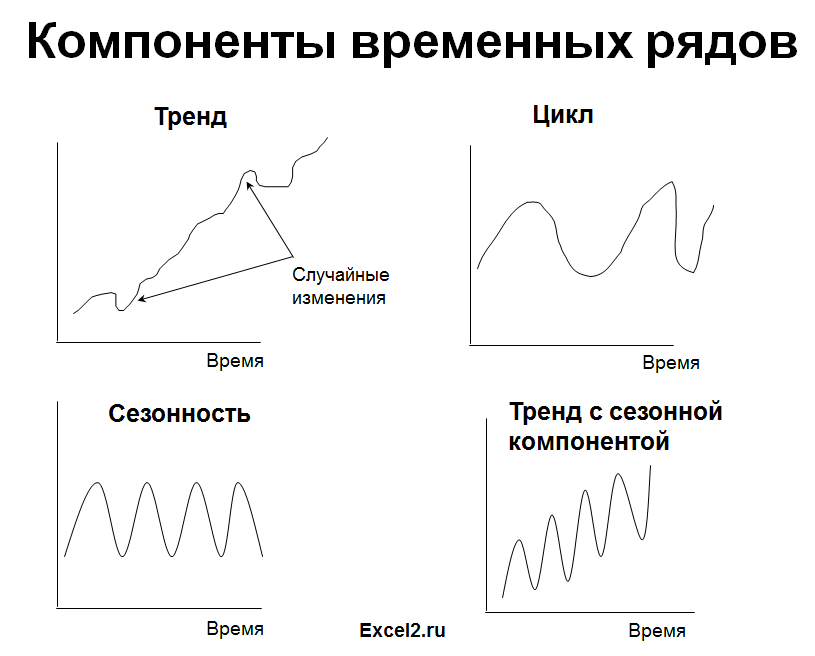
1. Стационарный процесс

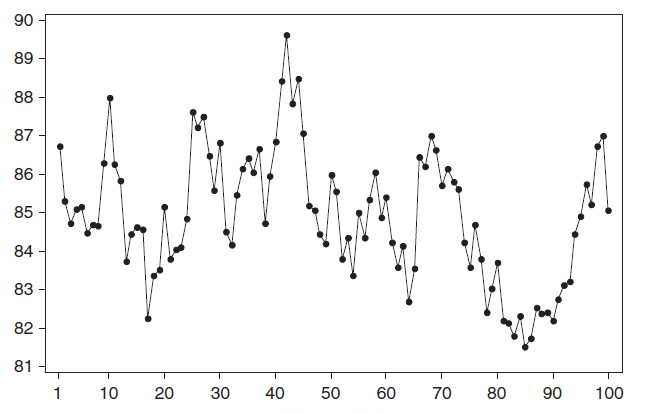
Стационарный процесс – это случайный процесс чьи характеристики не зависят от времени их наблюдения. Этими характеристиками являются среднее значение , дисперсия и автоковариация. В стационарном процессе не могут быть выделены предсказуемые паттерны. Соответственно ряды демонстрирующие тренд и сезонность - не стационарны. А вот ряд с цикличностью (апериодической) является стационарным, т.к. на долгосрочном временном интервале появление циклов предсказать невозможно.

Почему стационарный процесс важен? Так как стационарность подразумевает нахождение процесса в состоянии статистической стабильности, то такие временные ряды имеют постоянное среднее значение и дисперсию, которые определяются стандартным образом.

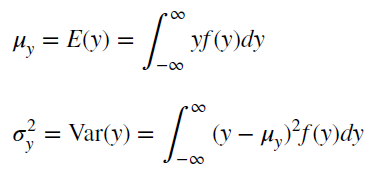
Также для стационарного процесса определяется функция автокорреляции – совокупность коэффициентов корреляции значений временного ряда с собственными значениями, сдвинутыми по времени на один или несколько периодов. Сдвиг на несколько временных периодов часто называется лагом (обозначается k).

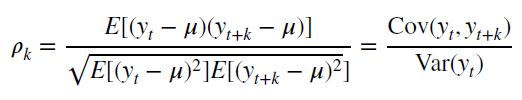
Функция автокорреляции является важным источником информации о временном ряде.

Примером стационарного процесса является колебания биржевого индекса, состоящего из стоимости акций нескольких компаний, около определённого значения (в период стабильности рынка).

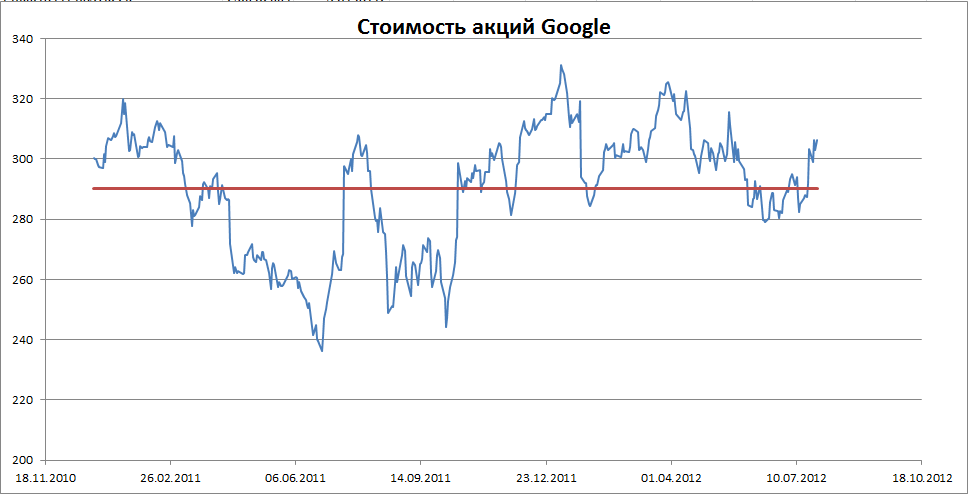
Примечание : график стоимости акций построен на реальных данных, см. файл примера Google .

Специальным видом стационарного процесса является белый шум. У этого процесса: среднее значений ряда равно 0, имеется конечная дисперсия и отсутствует корреляция между значениями исходного ряда и рядом сдвинутым на произвольное количество периодов (лагов). В MS EXCEL белый шум можно сгенерировать функцией СЛЧИС().

2. Линейный тренд

Некоторые процессы генерируют тренд (монотонное изменение значений ряда). Например, линейный тренд y=a*x+b, точнее y=a*t+b, где t – это время. Примером такого (не стационарного) процесса может быть монотонный рост стоимости недвижимости в некотором районе.

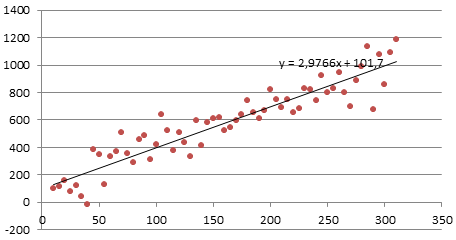
Для вычисления прогнозного значения можно воспользоваться методами Регрессионного анализа и подобрать параметры тренда: наклон и смещение по вертикали.

Примечание : Про генерацию случайных значений, демонстрирующих линейный тренд, можно посмотреть в статье Генерация данных для простой линейной регрессии в EXCEL .

3. Процессы, демонстрирующие сезонность

В сезонном процессе присутствует точно или примерно фиксированный интервал изменений, например, продажи некоторых товаров имеют четко выраженный пик в ноябре-декабре каждого года в связи с праздником.

Для прогнозирования вычисляется индекс сезонности, затем ряд очищается от сезонной компоненты. Если ряд также демонстрирует тренд, то после очистки от сезонности используются методы регрессионного анализа для вычисления тренда.

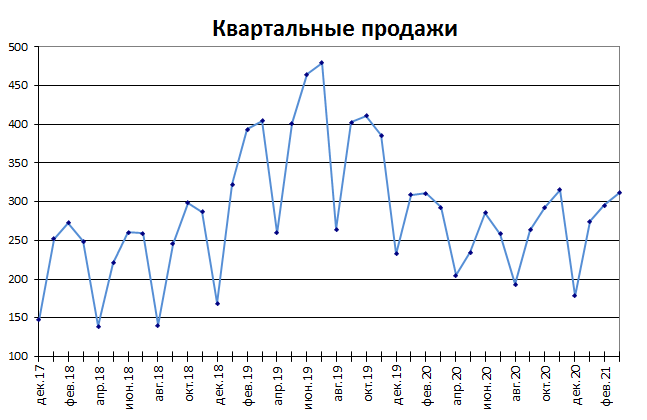
Примечание : Про генерацию случайных значений, демонстрирующих сезонность, можно посмотреть в статье Генерация сезонных трендов в EXCEL.

Часто на практике встречаются ряды, являющиеся комбинацией вышеуказанных типов тенденций.

О моделях прогнозирования

В качестве простейшей модели для прогноза можно взять последнее значение индекса. Этой модели соответствует следующий ход мысли исследователя: «Если значение индекса вчера было 306, то и завтра будет 306».

Этой модели соответствует формула Y _{прогноз(t)} = Y _t-1 (прогноз в момент времени t равен значению временного ряда в момент t-1).

Другой моделью является среднее за последние несколько периодов ( скользящее среднее ). Этой модели соответствует другой ход мысли исследователя: «Если среднее значение индекса за последние n периодов было 540, то и завтра будет 540». Этой модели соответствует формула Y _{прогноз(t)} =(Y _t-1 + Y _t-2 +…+Y _t-n )/n

Обратите внимание, что значения временного ряда берутся с одинаковым весом 1/n, то есть более ранние значения (в момент t-n) влияют на прогноз также как и недавние (в момент t-1). Конечно, в случае, если речь идет о стационарном процессе (без тренда), такая модель может быть приемлема. Чем больше количество периодов усреднения (n), тем меньше влияние каждого индивидуального наблюдения.

Третьей моделью для стационарного процесса может быть экспоненциальное сглаживание . В этом случае веса более ранних периодов будут меньше чем веса поздних. При этом учитываются все предыдущие наблюдения. Вес каждого последующего наблюдения больше на 1-α (Фактор затухания), где α (альфа) – это константа сглаживания (от 0 до 1).
Этой модели соответствует формула Y _{прогноз(t)} =α*Y _t-1 + α*(1-α)*Y _t-2 + α*(1-α)2*Y _t-3 +…)

Формулу можно переписать через предыдущий прогноз Y _{прогноз(t)} =α*Y _t-1 +(1- α)* Y _{прогноз(t-1)} = α*(Y _t-1 - Y _{прогноз(t-1)} )+Y _{прогноз(t-1)} = α*(ошибка прошлого прогноза)+ прошлый прогноз

При экспоненциальном сглаживании прогнозное значение равно сумме последнего наблюдения с весом альфа и предыдущего прогноза с весом (1-альфа). Этой модели соответствует следующий ход мысли исследователя: «Вчера рано утром я предсказывал, что индекс будет равен 500, но вчера в конце дня значение индекса составило 480 (ошибка составила 20). Поэтому за основу сегодняшнего прогноза я беру вчерашний прогноз и корректирую его на величину ошибки, умноженную на альфа. Параметр альфа (константа) я найду методом экспоненциального сглаживания».

Подробнее о методе прогнозирования на основе экспоненциального сглаживания можно найти в этой статье .

Полезный сигнал и шум

Из-за случайного разброса, присущему временному ряду, временной ряд представляют как комбинацию двух различных компонентов: полезного сигнала и шума (ошибки). Полезный сигнал следует одному из 3-х вышеуказанных типов процессов. Сигнал может быть смоделирован и соответственно спрогнозирован. Шум представляет собой случайные ошибки (со средним значением =0, отсутствием корреляции и с фиксированной дисперсией ).

Основной задачей моделирования идентификация полезного сигнала, имеющего определенный тренд, от непредсказуемого шума. Для этого как раз и используются Модели сглаживания.

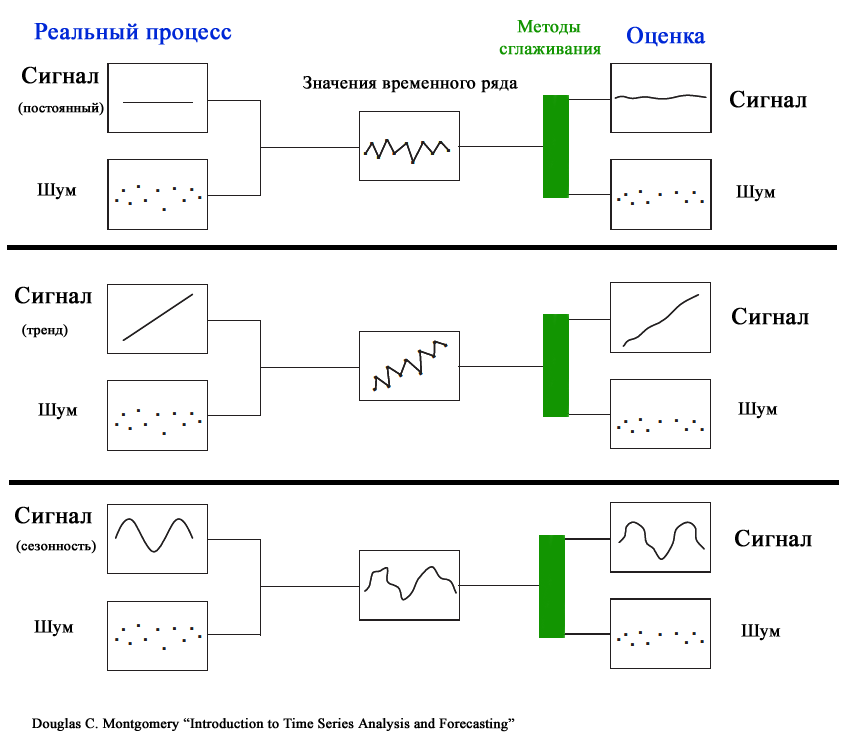
Ссылки на источники статистических данных и обучающие материалы

Все источники англоязычные.

Сайт о применении EXCEL в статистике
http://www.real-statistics.com/

Национальный Институт Стандартов и технологии
https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4.htm

Using R for Time Series Analysis
https://a-little-book-of-r-for-time-series.readthedocs.io/en/latest/src/timeseries.html#time-series-analysis

Учебник по прогнозированию временных рядов
https://otexts.com/fpp2/

Данные по болезням в Великобритании
https://ms.mcmaster.ca/~bolker/measdata.html

Курсы в Eberly College of Science (есть ссылки на базы данных)
https://online.stat.psu.edu/stat501/lesson/welcome-stat-501
https://online.stat.psu.edu/stat510/