Парный двухвыборочный t-тест для средних EXCEL
11 декабря 2016 г.
- Группы статей
- Статистический вывод
Рассмотрим использование MS EXCEL при проверке статистических гипотез о разнице средних значений 2-х распределений в случае неизвестных дисперсий (парный тест). Вычислим значение тестовой статистики t 0 , рассмотрим соответствующую процедуру «двухвыборочный t -тест», вычислим Р-значение (Р- value ). С помощью надстройки Пакет анализа сделаем «Парный двухвыборочный t-тест для средних».
Здесь рассмотрен специальный случай двухвыборочного t-теста , когда наблюдения случайных величин из двух распределений производятся не независимо, а парами.
Примечание : Процедура двухвыборочного t-теста также изложена в статьях Двухвыборочный t-тест с одинаковыми дисперсиями и Двухвыборочный t-тест с различными дисперсиями , где выборки из распределений считались независимыми.
СОВЕТ : При первом знакомстве с процедурой двухвыборочного t -теста может быть полезным освежить в памяти процедуру одновыброчного t-теста для среднего при неизвестной дисперсии .
СОВЕТ : Для проверки гипотез нам потребуется знание следующих понятий:
- дисперсия и стандартное отклонение ,
- выборочное распределение статистики ,
- уровень доверия/ уровень значимости ,
- нормальное распределение ,
- t-распределение Стьюдента и его квантили .
Приведем пример . Имеется 2 прибора измеряющих твердость металлических образцов. Необходимо проверить, что эти приборы показывают одинаковые результаты на одном и том же образце ( нулевая гипотеза ).
Если для испытания на приборах образцы отбирать случайным образом: половину для проверки на приборе №1, другую на приборе №2, и использовать для проверки нулевой гипотезы t-тест с одинаковыми (или различающимися) дисперсиями, то можно сделать ошибочное заключение. Дело в том, что металлические образцы могут быть изготовлены из различных заготовок, прошедших различную термообработку и, следовательно, они могут иметь различную твердость. Таким образом, наблюденная разность между средними значениями твердости, полученными на каждом из приборов (Х ср1 и Х ср2 ), будет также включать различие в твердости, обусловленную самими образцами. Другими словами, при таком методе исследования у нас имеется 2 источника неопределенности (случайности): несовершенство приборов и случайные колебания твердости самих образцов.
Чтобы исключить случайность, обусловленную различием образцов, и тем самым увеличить мощность t -теста , используют парные выборки . В нашем случае, измерения одного и того же образца будем проводить сначала на одном, затем на другом приборе (предполагается, что после измерения твердости на первом приборе, образец не портится).
Таким образом, процедура проверки гипотезы сводится к определению разности твердостей полученных приборами на одном и том же образце. Если приборы настроены одинаково, то среднее разностей должно быть около 0 (отклонение не должно быть статистически значимым).
Пусть имеется набор из n пар наблюдений (n образцов). Т.к. результат каждого наблюдения является случайной величиной (приборы не идеальны, присутствует случайная ошибка измерений), то эти случайные величины имеют распределения с неизвестными средними значениями μ 1 и μ 2 (измерения полученные на приборе №1 и №2, соответственно). Дисперсии этих распределений неизвестны (обозначим их σ 1 2 и σ 2 2 ).
Будем рассматривать не сами наблюдения, а их разницу. Обозначим D i – разницу измерений, полученную приборами №1 и №2 на i-м образце. Разницу между μ 1 и μ 2 , которую нам необходимо оценить, обозначим μ D .
Проведем проверку гипотезы о равенстве μ D заданному значению Δ 0 , т.е. парный t -тест (англ. The Paired t-Test). Если Δ 0 равно 0, то речь идет о проверке равенства средних двух распределений.
На самом деле, этот t -тест сводится к одновыборочному t-тесту :
- Нулевая гипотеза H 0 : μ D =Δ 0
- Альтернативная гипотеза H 1 : μ D <>Δ 0
Т.е. нам требуется проверить двухстороннюю гипотезу .
Тестовой статистикой является случайная величина t:
где D ср – среднее значение разностей, S d – стандартное отклонение этих разностей.
Как известно из статьи про одновыборочный t-тест , данная тестовая статистика , имеет t-распределение c n-1 степенью свободы. Значение, которое приняла эта t -статистика, обозначим t 0 .
Установим требуемый уровень значимости α (альфа) = 0,05 (допустимую для данной задачи ошибку первого рода , т.е. вероятность отклонить нулевую гипотезу , когда она верна).
Если вычисленное на основе выборок значение t 0 , в случае двухсторонней гипотезы , не попадет в область значений ограниченной нижним и верхним α/2-квантилями t - распределения с n–1 степенями свободы, то у нас будет основание отвергнуть нулевую гипотезу. Это утверждение эквивалентно случаю, когда D ср окажется вне пределов соответствующего доверительного интервала. В файле примера на листе Парный тест показана эквивалентность доверительного интервала и соответствующего t -теста.
Примечание : Верхний α/2-квантиль - этотакое значение случайной величины t n–1 , что P ( t n-1 >=t α/2 , n-1 ) =α/2. Верхний α/2-квантиль t - распределения с n -1 степенью свободы обычно обозначают t α /2, n-1 . Подробнее о квантилях распределений см. статью Квантили распределений MS EXCEL .
В нашем случае, необходимо будет вычислить только верхний α/2-квантиль, т.к. он равен соответствующему нижнему квантилю со знаком минус. Следовательно, условие отклонения нулевой гипотезы можно записать как |t 0 |>t α/2 , n-1 .
Чтобы в MS EXCEL вычислить значение t α/2 , n-1 для различных уровней значимости (10%; 5%; 1%) и степеней свобод можно использовать несколько формул: =СТЬЮДЕНТ.ОБР.2Х(α; n-1) =СТЬЮДЕНТ.ОБР(1- α/2; n-1) =-СТЬЮДЕНТ.ОБР(α/2; n-1) =СТЬЮДРАСПОБР(α; n-1)
Примечание : Подробнее про функции MS EXCEL, связанные с t - распределением см. статью t-распределение .
Итак, если при проверке двухсторонней гипотезы формула =ABS(t 0 ) вернет значение больше, чем результат формулы =СТЬЮДЕНТ.ОБР.2Х(α; n-1) , то это означает, что необходимо отвергнуть нулевую гипотезу (вычисления приведены в файле примера на листе Парный тест ) .
Для односторонней альтернативной гипотезы μ D >Δ 0 , нулевая гипотеза будет отвергнута в случае t 0 > t α , n-1 .
Для односторонней альтернативной гипотезы μ D <Δ 0 , нулевая гипотеза будет отвергнута в случае t 0 <-t α , n-1 .
Примечание : Вышеуказанные распределения не обязательно должны быть нормальными . Однако, требуется чтобы выполнялись условия применимости Центральной предельной теоремы . Если размеры выборок меньше 30, то для справедливости сделанных здесь выводов, необходимо, чтобы выборки были сделаны из нормального распределения .
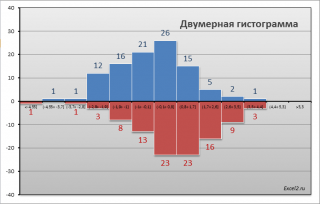
СОВЕТ : Перед проверкой гипотез о равенстве средних значений полезно построить двумерную гистограмму , чтобы визуально определить центральную тенденцию и разброс данных в обеих выборок .
Р-значение
При проверке гипотез, помимо t -теста, большое распространение получил еще один эквивалентный подход, основанный на вычислении p -значения (p-value).
Если p-значение меньше чем заданный уровень значимости α , то нулевая гипотеза отвергается и принимается альтернативная гипотеза . И наоборот, если p-значение больше α, то нулевая гипотеза не отвергается.
В случае двусторонней гипотезы p-значение равно суммарной вероятности, что t -статистика примет значение больше |t 0 | и меньше -|t 0 |.
Подробнее про p -значение см., например, статью про двухвыборочный z-тест .
В MS EXCEL p -значение для двухсторонней гипотезы в случае парного t -теста вычисляется по формуле: =2*(1-СТЬЮДЕНТ.РАСП(ABS(t 0 ); n-1;ИСТИНА))
Примечание : Вычисления приведены в файле примера на листе Парный тест .
Для односторонней гипотезы μ 1 -μ 2 >Δ 0 p -значение вычисляется по формуле: =1-СТЬЮДЕНТ.РАСП(t 0 ; n-1;ИСТИНА) В этом случае p-значение равно вероятности, что t -статистика примет значение больше t 0 .
Для односторонней гипотезы μ 1 -μ 2 <Δ 0 p -значение вычисляется по формуле: = СТЬЮДЕНТ.РАСП(t 0 ; n-1;ИСТИНА) В этом случае p-значение равно вероятности, что t -статистика примет значение меньше t 0 .
В файле примера на листе Парный тест показана эквивалентность проверки гипотезы через доверительный интервал , статистику t 0 ( t -тест) и p -значение .
В MS EXCEL есть функция СТЬЮДЕНТ.TEСT() , которая вычисляет p-значение для 3-х различных двухвыборочных t -тестов (см. следующий раздел статьи) . К сожалению, эта функция может быть использована только для проверки гипотез с Δ 0 =0, то есть для проверки гипотез о равенстве средних μ 1 =μ 2 . Об этом легко догадаться, т.к. среди ее параметров отсутствует параметр Гипотетическая разность средних , т.е. Δ 0 .
Функция СТЬЮДЕНТ.ТЕСТ()
Функция СТЬЮДЕНТ.ТЕСТ() используется для оценки различия двух выборочных средних . До MS EXCEL 2010 имелась аналогичная функция ТТЕСТ() .
Примечание : В английской версии функция носит название T.TEST(), старая версия - TTEST().
Функция СТЬЮДЕНТ.ТЕСТ() имеет 4 параметра. Первые два – это ссылки на диапазоны ячеек, содержащие выборки из 2-х сравниваемых распределений.
Третий параметр имеет название «хвосты». Этот параметр задает тип проверяемой гипотезы: односторонняя (=1) или двухсторонняя (=2). Если мы проверяем двухстороннюю гипотезу , то смотрим, не попало ли значение тестовой статистики в один из 2-х хвостов соответствующего t-распределения . Если мы проверяем одностороннюю гипотезу (имеется ввиду гипотеза μ 1 <μ 2 ), то «хвост» всего один.
Как было сказано выше, эта функция вычисляет p -значение для 3-х различных двухвыборочных t -тестов . За это отвечает четвертый параметр функции, который принимает значения от 1 до 3:
- Парный двухвыборочный t-тест для средних;
- Двухвыборочный t-тест с одинаковыми дисперсиями ;
- Двухвыборочный t-тест с разными дисперсиями .
Таким образом, p -значение для двухсторонней гипотезы (равные дисперсии ) вычисляется по формуле (см. файл примера ): =СТЬЮДЕНТ.ТЕСТ( выборка1 ; выборка2 ; 2; 1) или =2*(1-СТЬЮДЕНТ.РАСП(ABS(t 0 ); n-1;ИСТИНА))
Для односторонней гипотезы μ 1 <μ 2 p -значение вычисляется по формуле: =СТЬЮДЕНТ.ТЕСТ( выборка1 ; выборка2 ; 1; 1) или =СТЬЮДЕНТ.РАСП(t 0 ; n-1;ИСТИНА)
Для односторонней гипотезы μ 1 >μ 2 p -значение вычисляется по формуле: =1-СТЬЮДЕНТ.ТЕСТ( выборка1 ; выборка2 ; 1; 1) или =1-СТЬЮДЕНТ.РАСП(t 0 ; n-1;ИСТИНА)
Пакет анализа
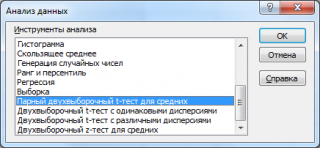
В надстройке Пакет анализа для проведения Парного двухвыборочного t -теста имеется одноименный инструмент: Парный двухвыборочный t -тест для средних (t-Test: Paired Two-Sample for Means).
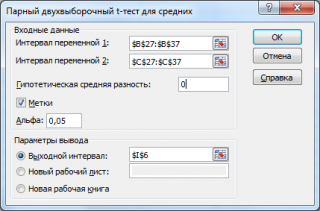
После выбора инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Пакет анализа ):
- интервал переменной 1 : ссылка на значения первой выборки . Ссылку указывать лучше с заголовком. В этом случае, при выводе результата надстройка выводит заголовки, которые делают результат нагляднее (в окне требуется установить галочку Метки );
- интервал переменной 2 : ссылка на значения второй выборки ;
- гипотетическая средняя разность : укажите значение Δ 0 , т.е. μ 1 -μ 2 . В нашем случае, введем 0;
- Метки: если в полях интервал переменной 1 и интервал переменной 2 указаны ссылки вместе с заголовками столбцов, то эту галочку нужно установить. В противном случае надстройка не позволит провести вычисления и пожалуется, что « входной интервал содержит нечисловые данные »;
- Альфа: уровень значимости ;
- Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
В результате вычислений будет заполнен указанный Выходной интервал.
Тот же результат можно получить с помощью формул (см. файл примера лист Пакет анализа ):
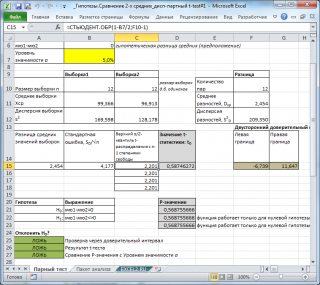
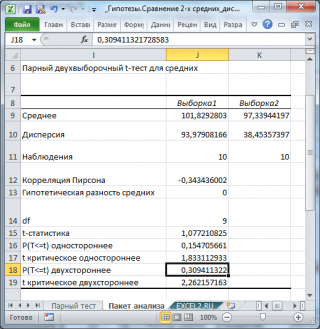
Разберем результаты вычислений, выполненных надстройкой:
- Среднее : средние значения обеих выборок Хср 1 и Хср 2 . Вычисления можно сделать с помощью функции СРЗНАЧ() ;
- Дисперсия : дисперсии обеих выборок. Вычисления можно сделать с помощью функции ДИСП.В()
- Наблюдения : размер выборок. Вычисления можно сделать с помощью функции СЧЁТ()
- Корреляция Пирсона : коэффициент корреляции двух выборок . Вычисления можно сделать с помощью функции КОРРЕЛ() или PEARSON()
- Df : число степеней свободы : n-1, где n размер выборок ;
- t -статистика : значение тестовой статистики t (в наших обозначениях – это t 0 ). Вычисление t 0 приведено в ячейке Е1 5 ;
- P(T<=t) одностороннее : р-значение в случае односторонней альтернативной гипотезы μ 1 -μ 2 >Δ 0 . Эквивалентная формула =1-СТЬЮДЕНТ.РАСП(t 0 ; n-1;ИСТИНА) ;
- t критическое одностороннее : Верхний α-квантиль t-распределения. Эквивалентная формула =СТЬЮДЕНТ.ОБР(1- α; n-1) ;
- P(T<=t) двухстороннее: р-значение в случае двухсторонней альтернативной гипотезы μ 1 -μ 2 <>Δ 0 . Эквивалентная формула =2*(1-СТЬЮДЕНТ.РАСП(ABS(t 0 ); n-1;ИСТИНА)) ;
- t критическое двухстороннее: Верхний α/2-Квантиль t-распределения . Эквивалентная формула =СТЬЮДЕНТ.ОБР(1- α/2; n-1) .
СОВЕТ : О проверке других видов гипотез см. статью Проверка статистических гипотез в MS EXCEL .
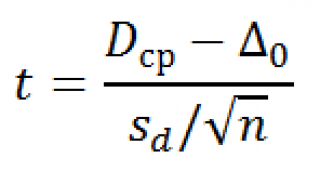
Комментарии