Гамма распределение. Непрерывные распределения в EXCEL
9 ноября 2016 г.
- Группы статей
- Распределения вероятностей
Рассмотрим Гамма распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ГАММА.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров распределения.
Гамма распределение (англ. Gamma distribution ) зависит от 2-х параметров: r (определяет форму распределения) и λ (определяет масштаб). Плотность вероятности этого распределения задается следующей формулой:
где Г(r) – гамма-функция:
если r – положительное целое, то Г(r)=(r-1)!
СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
Вышеуказанная форма записи плотности распределения наглядно показывает его связь с Экспоненциальным распределением . При r=1 Гамма распределение сводится к Экспоненциальному распределению с параметром λ.
Если параметр λ – целое число, то Гамма распределение является суммой r независимых и одинаково распределенных по экспоненциальному закону с параметром λ случайных величин x . Таким образом, случайная величина y = x 1 + x 2 +… x r имеет гамма распределение с параметрами r и λ.
Экспоненциальное распределение , в свою очередь, тесно связано с дискретным распределением Пуассона . Если Распределение Пуассона описывает число случайных событий, произошедших за определенный интервал времени, то Экспоненциальное распределение, в этом случае,описывает длину временного интервала между двумя последовательными событиями.
Из этого следует, что, например, если время до наступления первого события описывается экспоненциальным распределением с параметром λ, то время до наступления второго события описывается гамма распределением с r = 2 и тем же параметром λ.
Гамма распределение в MS EXCEL
В MS EXCEL принята эквивалентная, но отличающаяся параметрами форма записи плотности гамма распределения .
Параметр α ( альфа ) эквивалентен параметру r , а параметр b ( бета ) – параметру 1/λ . Ниже будем придерживаться именно такой записи, т.к. это облегчит написание формул.
В MS EXCEL, начиная с версии 2010, для Гамма распределения имеется функция ГАММА.РАСП() , английское название - GAMMA.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и интегральную функцию распределения (вероятность, что случайная величина X, имеющая гамма распределение , примет значение меньше или равное x).
Примечание : До MS EXCEL 2010 в EXCEL была функция ГАММАРАСП() , которая позволяет вычислить интегральную функцию распределения и плотность вероятности . ГАММАРАСП() оставлена в MS EXCEL 2010 для совместимости.
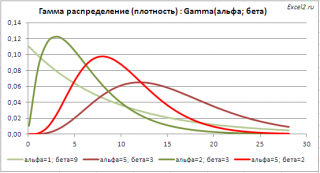
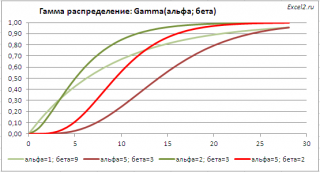
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Гамма распределение имеет обозначение Gamma (альфа; бета).
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Примечание : Для удобства написания формул в файле примера для параметров распределения альфа и бета созданы соответствующие Имена .
Примечание : Зависимость от 2-х параметров позволяет построить распределения разнообразных форм, что расширяет применение этого распределения. Гамма распределение , как и Экспоненциальное распределение часто используется для расчета времени ожидания между случайными событиями. Кроме того, возможно использование применение этого распределения для моделирования уровня осадков и при проектировании дорог.
Как было показано выше, если параметр альфа = 1, то функция ГАММА.РАСП() возвращает экспоненциальное распределение с параметром 1/бета . Если параметр бета = 1, функция ГАММА.РАСП() возвращает стандартное гамма распределение .
Примечание : Т.к. ХИ2-распределение является частным случаем гамма распределения , то формула =ГАММА.РАСП(x;n/2;2;ИСТИНА ) для целого положительного n возвращает тот же результат, что и формула =ХИ2.РАСП(x;n; ИСТИНА) или =1-ХИ2.РАСП.ПХ(x;n) . А формула =ГАММА.РАСП(x;n/2;2;ЛОЖЬ) возвращает тот же результат, что и формула =ХИ2.РАСП(x;n; ЛОЖЬ) , т.е. плотность вероятности ХИ2-распределения.
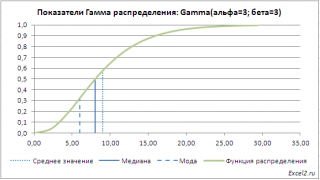
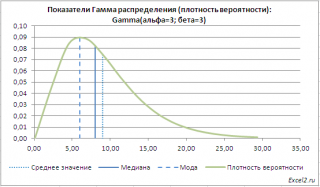
В файле примера на листе Графики приведен расчет Среднего значения (математического ожидания) гамма распределения равного альфа*бета и дисперсии (квадрата стандартного отклонения) равного альфа*бета 2 . Там же построены графики функции распределения и плотности вероятности с отмеченными значениями среднего , медианы и моды .
Генерация случайных чисел и оценка параметров
Для генерирования массива чисел, имеющих гамма распределение , можно использовать формулу
=ГАММА.ОБР(СЛЧИС(); альфа; бета) Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Если случайные числа содержатся в диапазоне B15:B214 , то оценку параметра альфа можно сделать с использованием формулы =СРЗНАЧ(B15:B214)^2/ДИСП.В(B15:B214)
Для оценки параметра бета используйте формулу =ДИСП.В(B15:B214)/СРЗНАЧ(B15:B214)
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
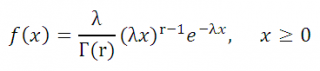
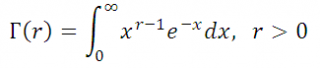
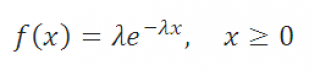
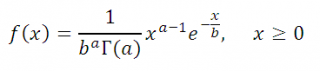
Комментарии