Генерация данных для простой линейной регрессии в EXCEL

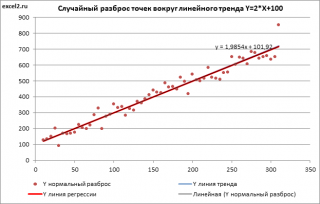
Сгенерируем массив данных для целей простой линейной регрессии. Линейный тренд зададим уравнением: Y = k * X + m .

Для академических целей бывает полезно сгенерировать в MS EXCEL значения двух переменных, которые демонстрируют приблизительно линейную взаимосвязь (см. статью про линейную регрессию ).

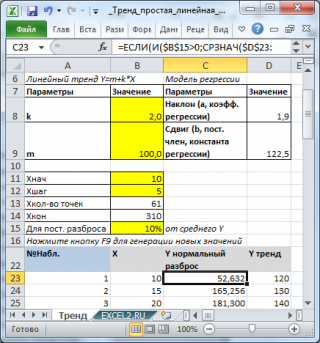
Для этого нам понадобятся следующие исходные данные:

• наклон k и сдвиг m для задания линии тренда: Y=k*X+m (не путать их с оценками параметров регрессионной модели );
• начальное значение Х и шаг изменения Х (шаг будет равномерный);
• величина разброса (в процентах от среднего значения Y).

Сначала сгенерируем массив значений Х и Y = k * X + m (см. файл примера столбцы B и D ).

Линию тренда построим на диаграмме типа Точечная по 2-м точкам, т.к. в этом случае линия выглядит на диаграмме ровнее, по сравнению с тем, если ее строить по всем точкам.

В принципе, линию тренда можно построить и на диаграмме типа График , однако, в этом случае может возникнуть проблема с линией регрессии, построенной с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Проблема касается корректного отображения уравнения тренда (подробнее см. в статье про Простую линейную регрессию в разделе Построение линии регрессии ).

Генерацию случайного разброса точек будем производить нормальному закону . Для этого необходимо использовать функцию НОРМ.ОБР() .

=ЕСЛИ(И($B$15>0;СРЗНАЧ($D$23:$D$83));

НОРМ.ОБР(СЛЧИС();D23;$B$15*ABS(СРЗНАЧ($D$23:$D$83)));

D23)

В качестве среднего значения (второй аргумент функции НОРМ.ОБР() ) будем брать текущее значение Y тренда ( D23 ). В качестве стандартного отклонения используем среднее значение Y, умноженное на заданный % отклонения. Подробнее о генерации случайных значений по нормальному закону см. в статье про случайные значения, распределенные по нормальному закону .

Для наглядности также построим линию регрессии (с помощью инструмента Линия тренда и с помощью формул (столбец F ), предварительно вычислив параметры модели).

Обе линии (регрессии и тренда) не обязательно будут совпадать.