Для построения статистических моделей часто требуются наборы случайных данных, которые бы содержали нужный тип тренда. Их можно найти в открытом доступе (например, в этой статье ), но иногда их удобно быстро сгенерировать самостоятельно.

Сезонные тренды на основе ломаных линий

Зададим сезонный тренд с помощью нескольких прямых линий (см. файл примера ).

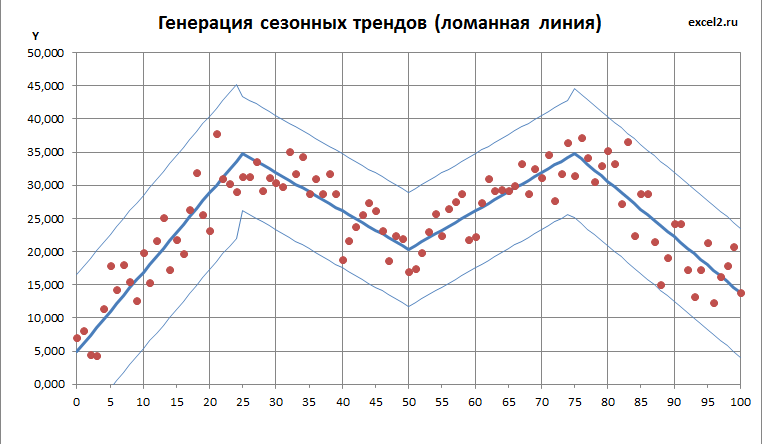
Как известно, уравнение прямой линии y=a*x+b. Чтобы задать прямую линию нужно 2 параметра: наклон прямой к оси Х (параметр а, он также является тангенсом угла наклона прямой к оси Х) и координата пересечения прямой с осью Y (параметр b).

В файле примера , вместо параметра b мы будем задавать координаты по оси Х, в которых происходит излом прямой линии – это удобнее. Для первой линии придется все же задать параметр b, для других отрезков ординату точки пересечения прямой линией оси Y (оси ординат), т.е. параметр b, будем вычислять. Наклон будем задавать, указывая угол в градусах (острый угол – восходящий тренд: 30, 45, 60 и т.п., отрицательные значения – для тупого угла (нисходящий тренд)).

Построение ломаной линии тренда и границ разброса

Для этого чтобы вычислить tg угла наклона (параметр а ) нам понадобится формула = TAN(РАДИАНЫ(G8)) . Функция TAN() воспринимает радианы, поэтому для перевода градусов в радианы используем функцию РАДИАНЫ() . Градусы в радианы можно перевести просто умножив значение в градусах на дробь ПИ()/180 .

Для разброса случайных значений вокруг линии тренда нам потребуется задать границы разброса. В файле примера в качестве меры разброса предложено использовать диапазон изменения величины Y первой линии тренда (для этого достаточно умножить тангенс угла наклона первой линии на диапазон изменения по Х первого отрезка). Используя вместо абсолютного значения диапазон изменения величины Y первой линии тренда, нам не потребуется вычислять величину разброса каждый раз, когда мы меняем тренда.

Примечание : диапазон изменения величины Y первой линии тренда не может быть равен 0, т.к. диапазон разброса будет также равен 0. Иными словами, первая линия не должна быть горизонтальной.

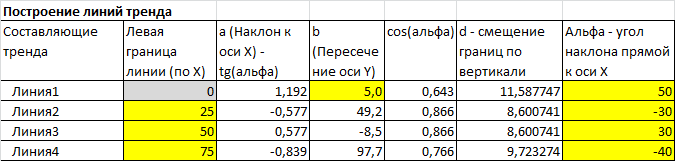
Чтобы иметь возможность менять границы разброса независимо от параметров первой линии тренда, в ячейке В14 введем коэффициент разброса K – это просто доля от диапазона изменения величины Y первого отрезка. Итак, пусть h - расстояние от линии тренда до верхней (или нижней) границы (в перпендикулярном к линии направлении), формула для вычисления h=a*∆x*K

Остается еще одна проблема – для разных линий, имеющих разный наклон нужно чтобы границы разброса отстояли от линии тренда на одну и туже величину h (в перпендикулярном к линии направлении). Для этого для каждой линии будем вычислять проекцию h на ось Y, назовем ее величиной d. Для этого используем формулу =h*COS(РАДИАНЫ(G8)), в ячейке находится G8 находится величина h.

Примечание : Для того чтобы на диаграмме EXCEL границы разброса отстояли от разных линий тренда визуально на одну и туже величину требуется, чтобы диаграмма имела одинаковый масштаб по Х и по Y. Если по Х откладывается время, а по Y, например, стоимость акции, то физический смысл «равенства» масштабов не понятен. Можно вообще пренебречь изменением границ разброса по Y в зависимости от угла наклона прямой – в этом случае не требуется вычислять величину d, просто используйте величину h. В файле примера масштабы осей совпадают и введен поправочный коэффициент COS(РАДИАНЫ(G8)) , поэтому диапазон разброса у всех отрезков ломаной линии тренда одинаков (это видно на рисунке выше).

С границами определились, переходим к построению точек, имитирующих разброс около линии тренда. Разброс значений случайной величины будем осуществлять с помощью нормального и равномерного распределения . Про генерацию случайных чисел можно прочитать здесь .

Равномерный разброс

Про равномерный разброс написана целая статья, здесь только укажем, что нам понадобится функция СЛУЧМЕЖДУ() , которая возвращает случайное целое число между заданных границ. Границы мы вычислили в предыдущем разделе, окончательная формула выглядит так: = СЛУЧМЕЖДУ(J19*10;K19*10)/10 , где J19 содержит координату Y нижней границы для заданного Х, а K19 – верхней. Умножение и деление на 10 нужно, чтобы результат возвращался не в целых числах, а с точностью до десятых. В этом случае точки будут размещаться более естественно, без стратификации (это зависит от диапазона изменения Y в каждой конкретной задаче).

Примечание : вместо функции СЛУЧМЕЖДУ() можно использовать СЛЧИС() , возвращающей случайное вещественное число от 0 до 1 .

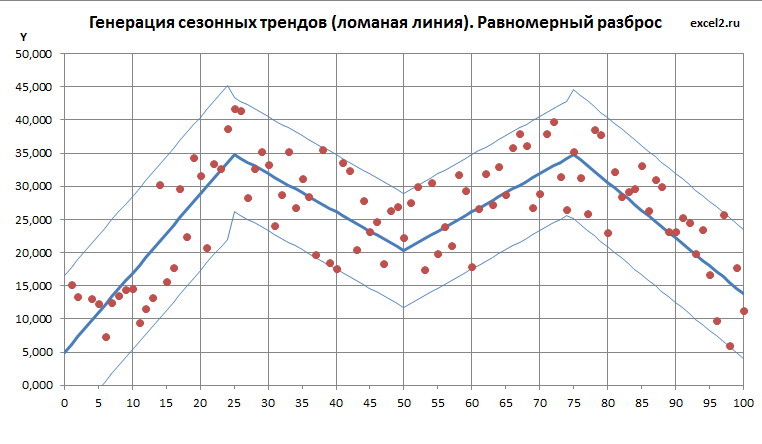
Как видно на картинке выше точки случайных значений равномерно распределены между границами, ни одна точка не может выйти за границы (вероятность этого события равна 0). Это принципиальное отличие от разброса по нормальному закону.

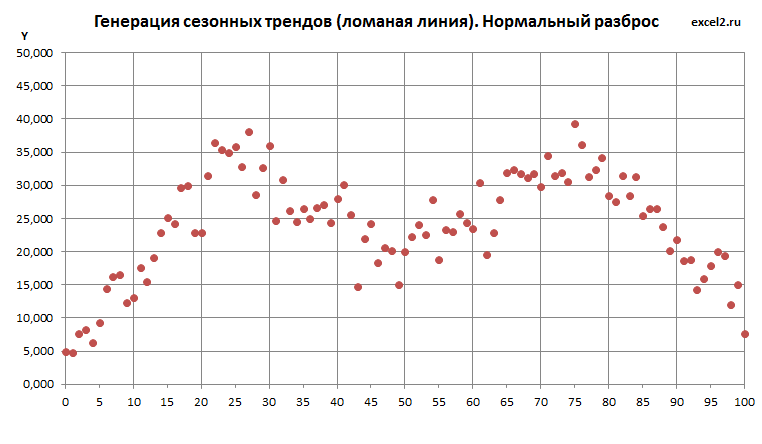
Нормальный разброс

Про нормальный разброс также написана целая статья . Нам понадобится функция НОРМ.ОБР() , которая возвращает значение случайной величины имеющей нормальное распределение (для указанного среднего и стандартного отклонения , а также заданной вероятности). В качестве среднего нужно взять линию тренда, точнее координату Y линии тренда для заданного Х. Т.к. известно, что 99,7% значений такой случайной величины находится на расстоянии не более 3 сигма  от среднего (сигма - стандартное отклонение), то в качестве стандартного отклонения логично взять 1/3 расстояния от тренда до границы (d).

Формула для генерации значений, имеющих нормальный разброс, выглядит так:
= НОРМ.ОБР(СЛЧИС();I19;ВПР(A19;$B$8:$F$11;5)/3)

Функция СЛЧИС() задает вероятность (от 0 до 1) того, что случайная величина, распределенная по заданному нормальному закону, менее или равна величине возвращаемой формулой. Подробнее про обратные функции см. в статье про квантили распределения . Функция ВПР() просто возвращает расстояние от тренда до границы.

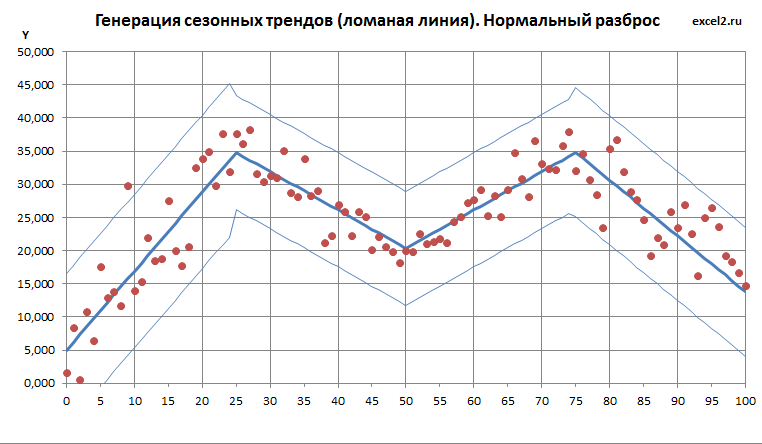
Как видно на картинке выше, точки случайных значений в основном находятся ближе к линии тренда, однако вероятность выхода точек за границы не равна 0 (точка с Х=9). Это принципиальное отличие от разброса по равномерному закону (см. предыдущий график).

Для отображения различных законов распределения в файле примера использован Элемент управления Переключатель .

Для скрытия тренда и/ или границ разброса использован Элемент управления Флажок .

После каждого изменения на листе (ввод значения, нажатие клавиши F9 или вставка значения в ячейку) функция СЛЧИС() заново генерирует новое значение, поэтому точки на диаграмме автоматически перестраиваются. Чтобы этого избежать отключите автоматический пересчет листа (в MS EXCEL 2010 это вкладка Формулы, группа Вычисления, кнопка Параметры вычислений).

Сезонные тренды на основе периодических функций

Построим сезонный тренд на основе 2-х периодических функций (синус) с добавлением линейного тренда.

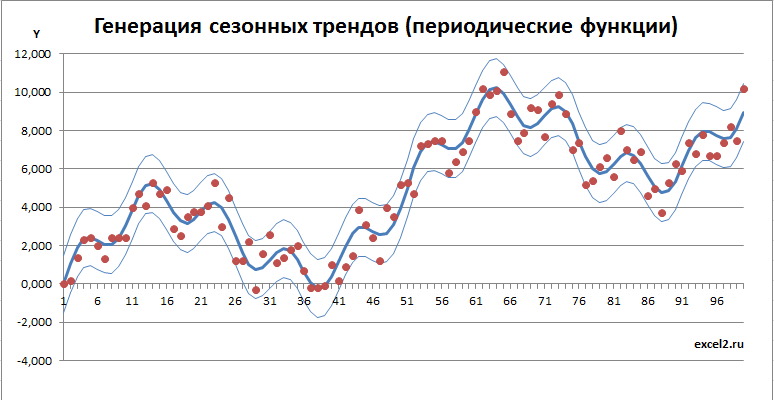
Всего будет 3 составляющих тренда:
•    Краткосрочный (на оси Х укладывается 8-10 циклов)
•    Долгосрочный (2-4 цикла с увеличенной амплитудой по сравнению с краткосрочным)
•    Линейный (восходящий или нисходящий)

Как и для тренда на основе ломаной линии разброс будет сделан по 2-м законам: равномерному и нормальному (см. файл примера ).

Краткосрочный тренд можно задать с помощью функции синус:
=SIN(2*ПИ()/100*A16*$B$7)

В ячейке B7 укажем число периодов функции синус, которое должно укладываться на всей оси Х диаграммы. 2*ПИ() – это значение периода функции синус. Деление на 100 (количество точек на диаграмме в файле примера, равномерно распределенных по оси Х) необходимо, чтобы на диаграмме разместилось целое количество периодов (для целых значений в ячейке В7, конечно). В целом, конечно, это больше для красоты.

Примечание : Чтобы на диаграмме в файле примера отображался только краткосрочный тренд установите 0 в ячейке С8 (масштаб долгосрочного тренда) и в ячейке В11 (наклон линейного тренда).

Долгосрочный тренд можно задать с помощью аналогичной формулы:
=$C$8*SIN(2*ПИ()/100*A16*$B$8)

В ячейке С8 указан масштаб долгосрочного тренда относительно амплитуды краткосрочного (равного 1).

Линейный тренд можно получить путем умножения координаты Х на константу.

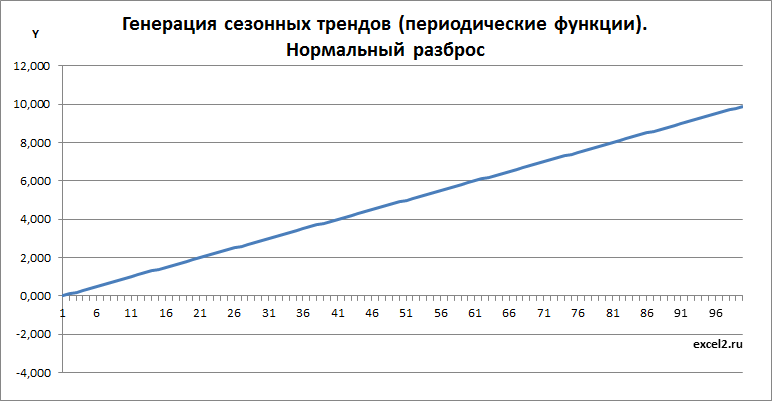
Арифметическая сумма трех составляющих тренда дает специфический тренд:

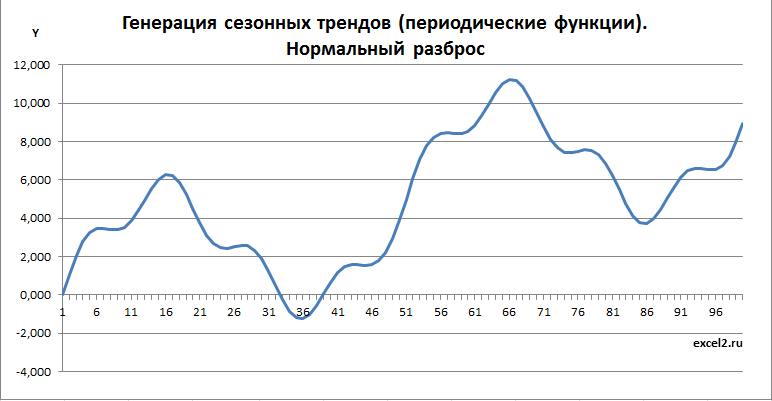
Добавив границы и точки, соответствующие случайным значениям, получим вот такую картинку.

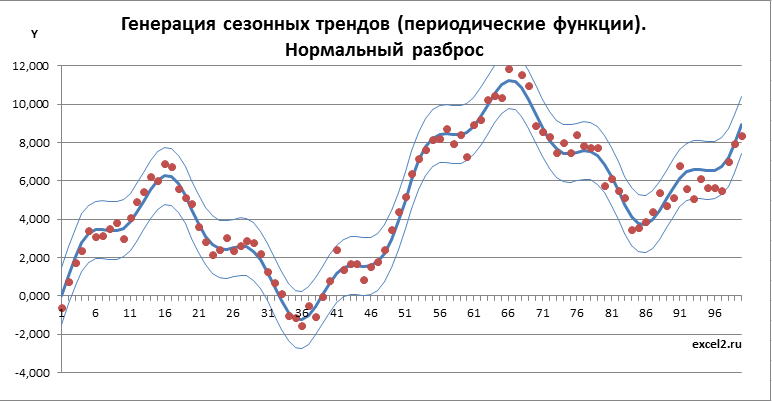
Если убрать границы, линию тренда, а также маркеры точек и соединить их линиями, то получим вот такой сезонный тренд.

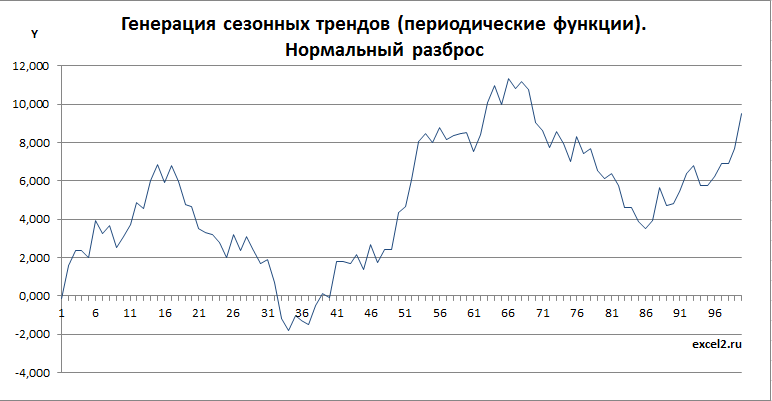
Добавив нужное количество точек и подобрав соотношение между краткосрочным и долгосрочным трендом, уверен, можно получить вполне реалистичную картинку, наподобие графика индекса S&P 500.