Краткое описание модели

Построим в MS EXCEL модель производственной линии, состоящей из 5 единиц оборудования. Каждая единица обрабатывает детали и передает дальше по цепочке пока не будет изготовлена готовая продукция.

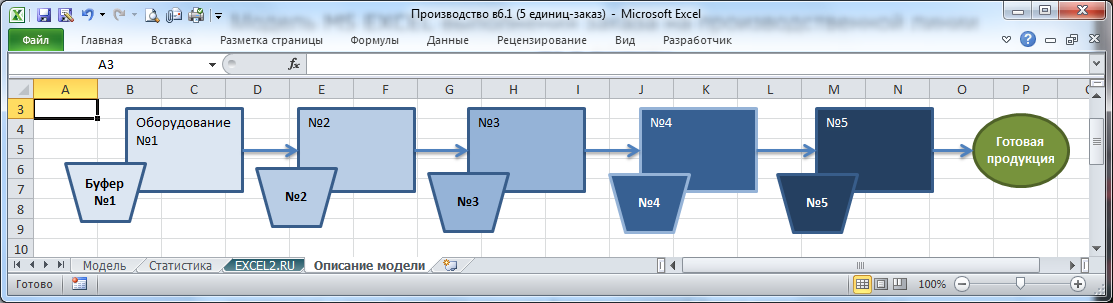
Оборудование может простаивать из-за поломки (задается вероятность выхода из строя оборудования и случайная величина длительности простоя ), также существует ненулевая вероятность получить брак при производстве деталей (совсем как в жизни).

Задается производительность оборудования (шт деталей/ час), как правило одна из единиц меньше по производительности, чем остальные. Эта единица называется Узким местом (bottleneck).

Поступивший заказ на изготовление N штук готовой продукции анализируется: вычисляется прогнозное время выполнения заказа и оценивается потребность в исходном сырье.

После нажатия кнопки "Запуск производства" сырье запускается в производство (выполняется программа на языке программирования VBA), на каждом временном шаге определяется работоспособность оборудования (не случилась ли поломка в соответствии с заданной вероятностью), а также вычисляется количество годных и бракованных изделий. Годные изделия, т.е. НЗП (незавершенное производство) передаются на следующий передел. Между оборудованием введены буферы для хранения НЗП. После завершения заказа выводится детальная информация о работе каждого оборудования и всей линии в целом (время простоя, полезная работа, количество брака и годных деталей, фактически потребленное сырье и время изготовления заказа). Строятся диаграммы.

Производительность линии определяется оборудованием с наименьшей производительностью (с учетом % брака) - Узким местом . Задача модели обеспечить Узкое место достаточным НЗП, чтобы оно не простаивало. Так как другие единицы оборудования имеют избыточную производительность, то в случае их бесперебойной работы буферы после них будут переполняться - в реальном производстве это будет приводить к увеличению инвестиций в оборотные средства. Поэтому модель позволяет ввести критический уровень буфера, после которого он перестает пополняться (предшествующая единица оборудования временно приостанавливает работу). Кроме того, модель минимизирует остаточный НЗП в системе (тот который остается после завершения выполнения заказа). Это достигается предварительным расчетом потребности в исходном сырье (статистический расчет при заданной вероятности брака и простоя).

Данная упрощенная модель работает только с единичным заказом, работа программы завершается сразу после того как этот заказ выполнен.

Набор статистики и оценка величин

У модели 2 основных задачи - оценить время исполнения заказа и спрогнозировать потребность в сырье для его выполнения. Поскольку обе этих величины являются случайными величинами (так как заданы ненулевые вероятности простоя и брака), то вычислить их точно невозможно. Можно лишь дать оценку среднего значения этих случайных величин. Для этого нужно оценить среднее и дисперсию неизвестного распределения этой случайной величины (см. эту статью о точечных оценках ).

Оценить среднее время исполнения заказа и среднее значение потребности в сырье можно, в принципе, обычными формулами зная % брака и вероятность простоя (это также реализовано в модели). Но, гораздо точнее набрать статистику и оценить эти величины статистическими методами. Кроме того, у нас появится возможность построить интервальную оценку (например, "Заказ будет выполнен в течение 120 часов с 95% вероятностью").

Для набора статистики модель прогоняет несколько десятков раз производство данного заказа и вычисляет среднее время выполнение заказа (количество прогонов задается в желтой ячейке Q6), а также время за которое заказ будет выполнен, скажем, с 95% вероятности. Аналогичные вычисления производятся и для оценки потребности в сырье.

Эти дополнительные вычисления с лихвой окупаются: после завершения "реального" производства с оцененным количеством исходного сырья, в НЗП остается (в среднем) материал примерно равный производительности системы за 1 шаг времени (как правило, в буфере перед последней единицы оборудования). Также мы знаем точность нашего предсказания времени изготовления заказа и можем, например, не только дать точечную оценку этой величины, но и построить доверительный интервал .

После изменения любого параметра системы (вероятность брака и простоя, длительность простоя, величина заказа, производительность оборудования) необходимо заново запускать набор статистики.

Как работать с программой

Программу можно скачать, нажав кнопку Файл примера внизу или вверху статьи.

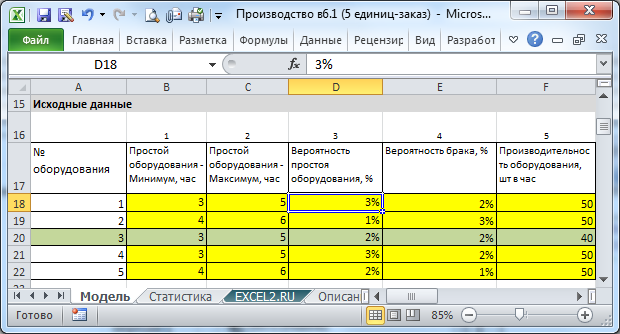
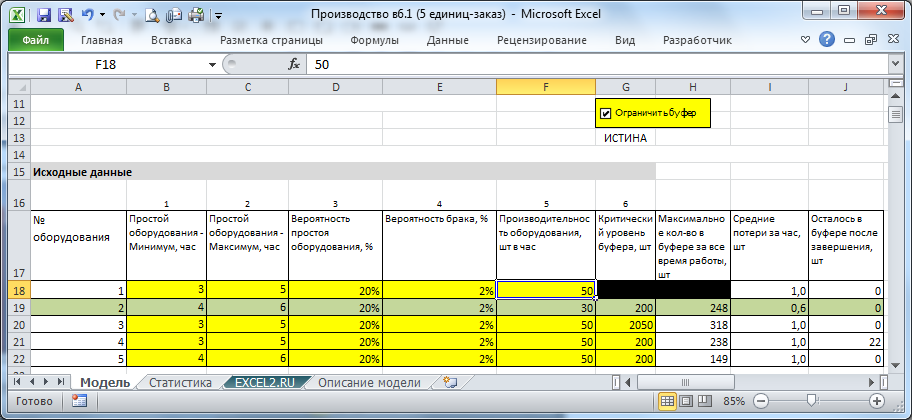
Шаг1: заполнить таблицу B18:G22 с исходными данными

Ячейки, которые требуют заполнения - выделены желтым. Основные данные, это конечно "Производительность оборудования, шт в час". При разработке модели предполагалось, что производительность оборудования отличается на 20-30%, максимум на 50%. Иначе, какой смысл объединять в производственную линию столь разное оборудование? При этом одна из единиц имеет минимальную производительность (узкое место) и определяет производительность всей системы. Можно, конечно задать всем машинам одинаковую производительность, или задать разницу по производительности в 200-300%  или определить 2 узких места - программа будет работать, но алгоритм затачивался именно на 1 узкое место.

Как было сказано выше, в модели полагается, что оборудование может простаивать, например из-за поломки, остановки на ремонт или отсутствия персонала (но не из-за отсутствия материала для обработки). В это время полезной работы не совершается. Вероятность такого простоя задается в % (на каждом временном шаге есть небольшая, например 2-3 %, вероятность того что машина работать не будет). Длительность простоя задается в часах (задается диапазон, например от 3 и до 5 часов). Конечно, в модели можно задавать любые разумные значения, но устанавливать вероятность более 20% вряд ли имеет смысл - что это за оборудование, если оно постоянно простаивает?

Даже если поломка не случилась, производственника ждет еще одна напасть - брак. Вероятность этого события также может быть любой разумной от 0 до 20%. Можно и больше задать, модель выдержит, но возникнет вопрос "Есть ли у Вас технология?".

Для того, чтобы наиболее производительные машины не производили горы незавершенной продукции, которые Узкое место не сможет перерабатывать в том же темпе, в программе можно задать "Критический уровень буфера, шт" выше которого предшествующая машина останавливает свое производство (на Узкое место это естественно не распространяется). Как только уровень НЗП понизится ниже этого уровня - машина вновь заработает. Данную опцию можно отключать с помощью флажка.

Также необходимо указать размер заказа - количество продукции, которое нужно изготовить. Обычно размер заказа выбирается таким образом, чтобы он был выполнен за 100-800 циклов (часов).

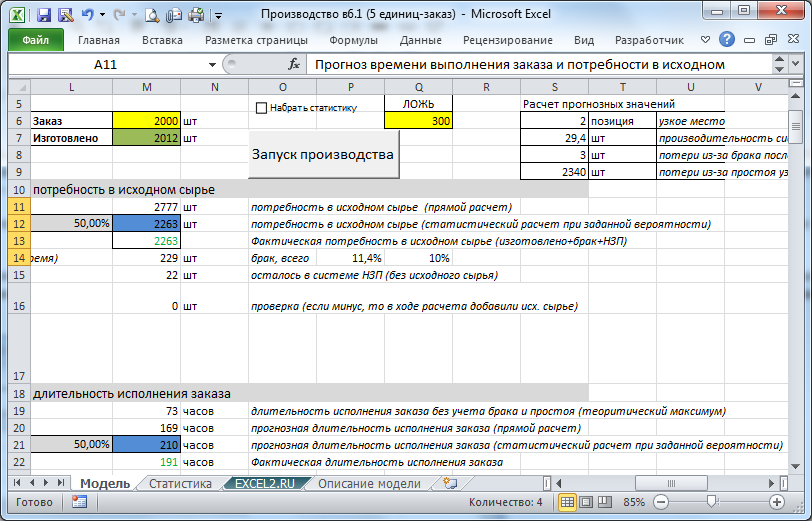
Шаг2. Набор статистики

Для того, чтобы оценить время выполнения заказа и потребность в исходном сырье потребуется набрать статистику, т.е. "прогнать" модель несколько десятков раз с заданными параметрами (вероятности брака и простоя, а также величины заказа). Поскольку в модели присутствуют случайные величины, каждый раз будут получаться слегка различные значения времени выполнения заказа и количества исходного сырья.

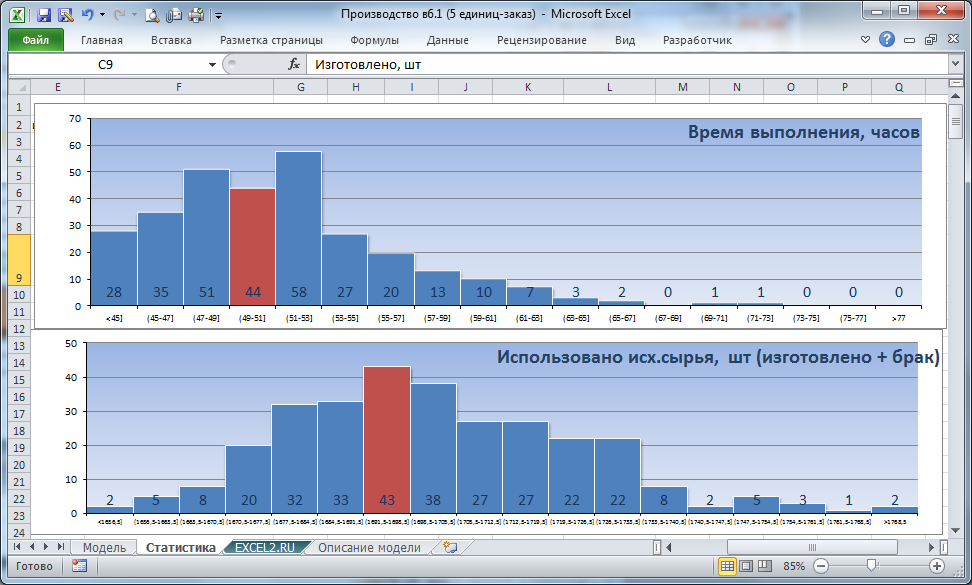
Для набора статистики нужно установить флажок "Набрать статистику" (связанная с ней ячейка Q5 отобразит значение ИСТИНА) и нажать кнопку Запуск производства. Через 5-7 секунд расчеты будут завершены и на листе Статистика будут построены гистограммы - это оценка плотности распределения случайных величин время выполнения заказа и количество исходного сырья.

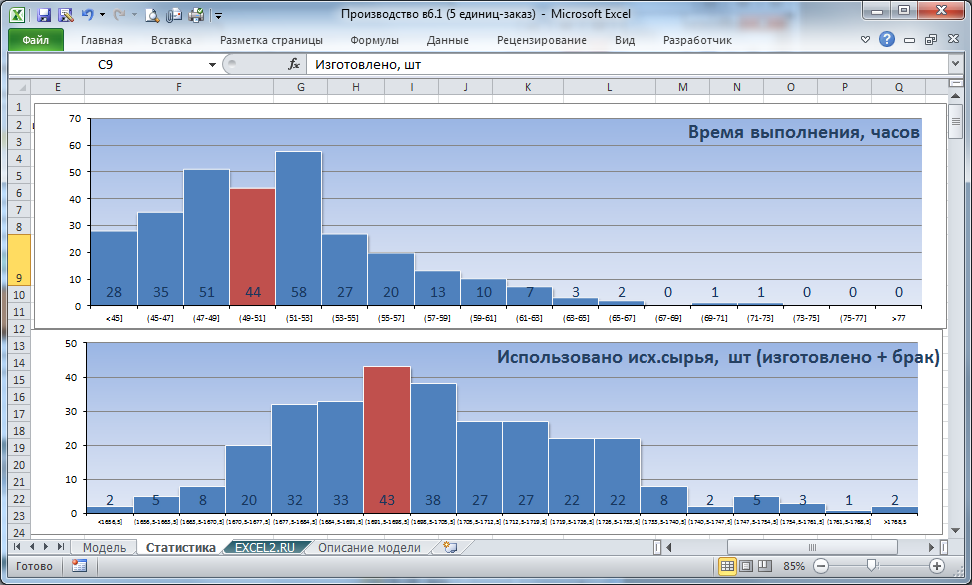
Теперь у нас есть не только средние значения этих величин, но и стандартное отклонение , позволяющего оценить степень разбросов около среднего .

Шаг3. Расчет и отображение результатов

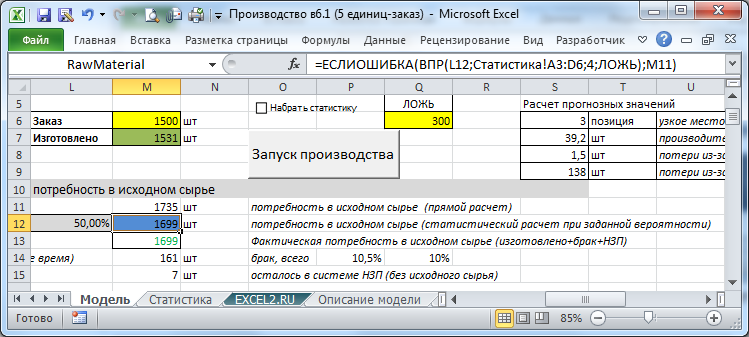
После завершения набора статистики переходим к моделированию. Для моделирования производственного процесса нужно снять флажок "Набрать статистику" (связанная с ней ячейка Q5 отобразит значение ЛОЖЬ) и нажать кнопку Запуск производства.

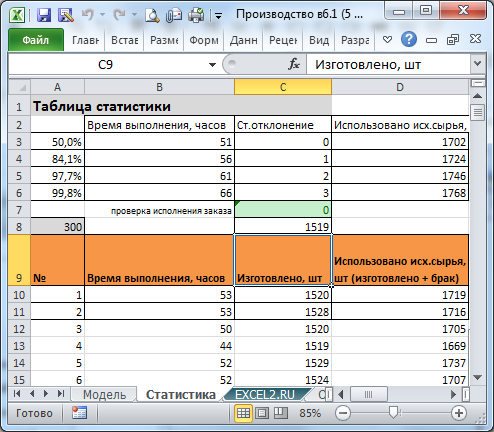
Как видно из картинки выше, прогнозные величины время выполнения заказа и количество исходного сырья (в синих ячейках) совпадают или близки к фактическим (зеленые ячейки и ячейки с числами, выделенные зеленым цветом шрифта). Так заказ выполнен с небольшим превышением в 5 шт, прогнозная потребность в исходном сырье совпала точно, а время исполнения отклонилось на 20 часов от среднего (258 против 278 прогнозных часов). Почему потребность в исходном сырье совпала, а время выполнения на 7% меньше? Дело в том, что стандартное отклонение величины количество исходного сырья составляет 24,6 шт (см. лист Статистика), что составляет 0,7% от среднего, а стандартное отклонение величины время выполнения заказа составляет 9% от среднего. Т.е. разброс второй величины значительно больше, что снижает точность прогнозирования. Почему разброс величины время выполнения заказа на порядок больше? Дело в том, что на разброс величины количество исходного сырья влияет только % брака, а на разброс величины время выполнения заказа влияет еще и вероятность простоя, а также случайная длительность простоя.

Подобные рассуждения о результатах модели позволяют определить факторы уже реальной производственной системы, на которые нужно воздействовать, чтобы повысить точность оценки предсказания/ исполнения заказа, сократить срок исполнения заказа или снизить НЗП. В нашем случае, для повышения точности прогнозирования заказа (и сокращения времени исполнения), очевидно, нужно снижать вероятность простоя. Для построения целевого ориентира программа позволяет смоделировать идеальную производственную систему, в которой нет простоев и/или брака.

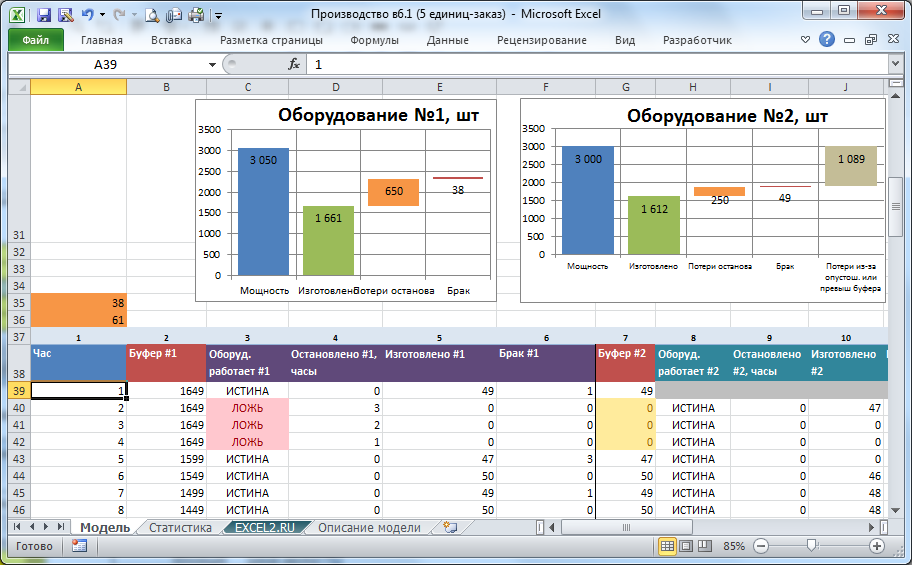
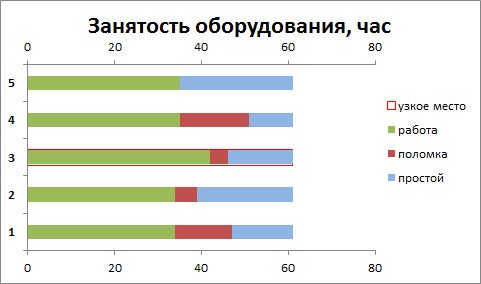
После завершения расчета на листе Модель для каждой единицы отображаются диаграммы, позволяющие оценить чем занималась конкретная единица в течение всего времени производства.

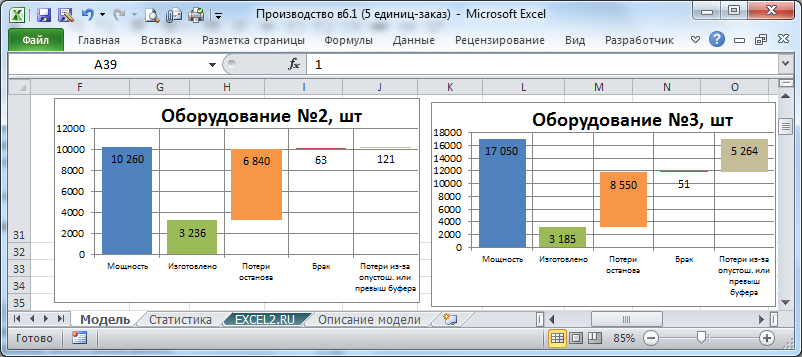
На диаграмме выше видно как различается работа "узкого места" (№2) и оборудования с более высокой производительностью (№3). Если узкое место не работало только из-за вынужденного останова, то оборудование №3 простаивало из-за опустошения предшествующего буфера или из-за превышения объемов наработанного НЗП в последующем буфере.

Также на листе доступна детальная расшифровка работы по каждому часу.

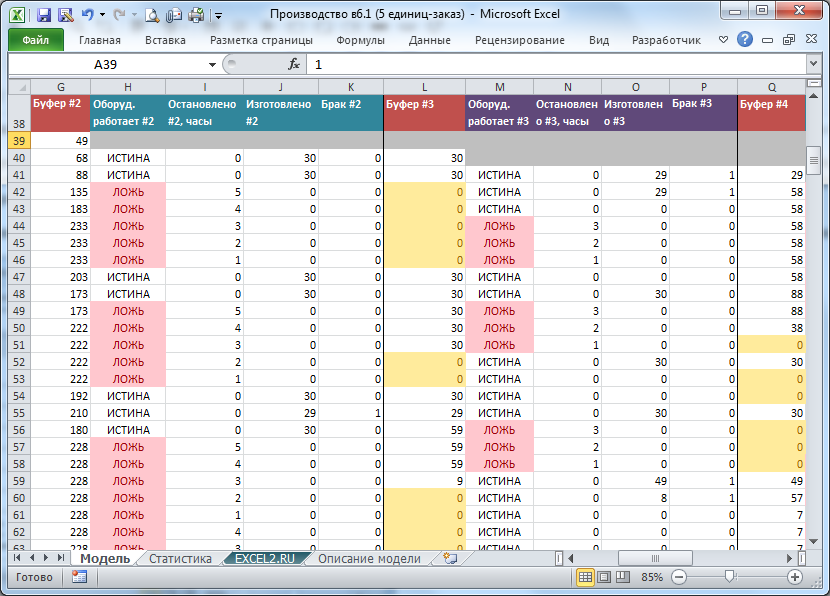
Реализация модели в MS EXCEL

Модель полностью построена на решениях MS EXCEL подробно описанных на сайте excel2.ru:

• построение диаграмм ,
• работа с функциями ,
• условное форматирование ,
• выпадающие списки ,
• именованные диапазоны ,
• элементы управления формы
• гистограмма распределения .

Так же рекомендуется иметь представление об Описательной статистике и Функции распределения .

Что дальше?

Данная программа имеет демонстрационные цели. Дальнейшее совершенствование возможно в следующих направлениях:

• вместо 1 заказа можно обрабатывать несколько, с указанием желаемого времени изготовления;
• реализовать систему "вытягивания" (в производство запускает ровно столько изделий, сколько востребовано заказами);
• сделать несколько различных продуктов, использовать разные типы полуфабрикатов;
• ввести операцию сборки изделия из разных полуфабрикатов и настраиваемую длину производственных цепочек;
• учесть рабочее время оборудования и наличие персонала;
• ввести в модель стоимостные параметры (цена ресурсов, стоимость 1ч работы оборудования;
• предложить варианты оптимизации производственной системы (максимизация пропускной способности системы, максимизация прибыли за период и т.д.)

Примечание : если требуется использовать данную модель для расчета производственной линии состоящей из двух, трех или четырех единиц оборудования, то нужно сделать производительность лишних единиц в разы больше, чем остальных.