Логнормальное распределение. Непрерывные распределения в EXCEL
8 ноября 2016 г.
- Группы статей
- Распределения вероятностей
Рассмотрим Логнормальное распределение. С помощью функции MS EXCEL ЛОГНОРМ .РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по логнормальному закону, произведем оценку параметров распределения, среднего значения и стандартного отклонения.
Если случайная величина Х имеет логнормальное распределение (англ. Lognormal distribution ) , то её логарифм Y=LN(X) имеет нормальное распределение . Справедливо и обратное утверждение: если случайная величина Y имеет нормальное распределение , то случайная величина X=EXP(Y) имеет логнормальное распределение . Из свойства логарифма следует, что X>0 (случайная величина Х, распределенная по логнормальному закону, может принимать только положительные значения).
Связь между нормальным и логнормальным распределениями.
Как известно, нормальное распределение чаще всего рассматривается как подходящая модель для описания такого процесса, когда действует большое число независимых случайных причин. Например, при производстве кускового мыла, вес каждого куска немного отличается от заданного в силу множества случайных причин, действующих на процесс: колебания температуры, состава исходного сырья, скачки напряжения на оборудовании и др. В этом случае плотность распределения случайной величины «вес мыла» имеет симметричную, колоколообразную форму.
Однако, в некоторых случаях наблюдения показывают, что случайная величина имеет заметно скошенное (несимметричное) распределение (см. раздел Ассиметричность в статье Описательная статистика в MS EXCEL ), и, соответственно, не может быть описана нормальным распределением . Скошенные распределения имеют место когда, случайные величины не могут быть отрицательными или имеется другая естественная граница (не может быть меньше определенного значения). Логнормальное распределение является одним из примеров скошенного распределения .
В чем же состоит различие в процессах, приводящих к нормальному или логнормальному распределениям? Оба распределения имеют место, когда на описываемый объект воздействует множество случайных и независимых факторов. Если воздействия каждого из факторов складываются, т.е. имеется аддитивный характер их взаимодействия, то имеет место нормальное распределение (см. статью про Центральную предельную теорему ).
Если воздействия каждого из факторов не складываются, а перемножаются, т.е. имеется мультипликативный характер взаимодействия, что часто соответствует Логнормальному распределению. Факторы также независимы как и в случае нормального распределения, но эффект от их воздействия накапливается в объекте в зависимости от предыдущего их количества.
Чтобы это пояснить, рассмотрим процесс износа подшипника. Понимание физического процесса позволит построить адекватную статистическую модель (распределение) и, в данном случае, оценить средний срок его работы до поломки.
Износ подшипника происходит из-за множества случайных независимых факторов: несовершенства формы шариков подшипника, внешних ударов, попадания грязи и пр. Пусть в определенный момент происходит случайное событие, например, удар, который приводит к микродефекту внешнего кольца удерживающего шарики, но поломка подшипника еще не происходит. Понятно, что с деформированным кольцом разрушение подшипника ускорится (например, за счет повышенного истирания). Теперь рассмотрим два вида взаимодействия воздействующих факторов: аддитивный и мультипликативный.
В первом случае, считается, что микродефекты просто складываются и поломка подшипника происходит при превышении некого порогового их воздействия (суммирование микродефектов). Т.е. в этой модели не учитывается, что каждый последующий микродефект воздействует уже не на новый подшипник, а на поврежденный.
Во втором случае (мультипликативное взаимодействие), каждый последующий микродефект воздействует на подшипник пропорционально его текущему состоянию. Т.е. одно и тоже воздействие будет приводить к разным последствиям (дефектам) в случае нового или уже поврежденного подшипника.
Как было сказано выше, модель аддитивного взаимодействия случайных факторов приводит к нормальному распределению (в данном случае она не применима для оценки срока работы подшипника). В нашем случае более адекватной моделью является модель мультипликативного взаимодействия, когда учитывается не только случайное воздействие фактора, но и состояние самой системы, на которую действует фактор. Мультипликативный эффект от всех случайных независимых воздействий на подшипник аккумулируется до тех пор пока не произойдет его разрушение.
Попытаемся вышесказанное изложить с помощью формул. По аналогии с ЦПТ и учитывая свойство логарифма LN ( x 1* x 2*…* xn )= LN ( x 1)+ LN ( x 2)+… +LN(x n ) , можно предположить, что если x1, x2, x3, … xn – случайные независимые величины, и y = x 1* x 2* x 3* … * xn , то случайная величина LN(y) будет распределена по нормальному закону . Если это условие выполняется, т.е. LN ( y ) ~ N (μ;σ) , то y имеет логнормальное распределение с параметрами μ и σ .
Примерами, когда имеет место логнормальное распределение могут служить следующие ситуации:
- сбой из-за химических реакций или деградации, таких как коррозия или диффузия, которые являются частой причиной отказа полупроводникового элемента;
- время до разрушения в металлах при условии роста усталостных трещин.
Ниже приведена функция плотности логнормального распределения :
СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
Обратите внимание, что хотя μ и σ являются параметрами распределения, они НЕ являются средним значением (обозначим среднее значение как μ Х ) и стандартным отклонением (обозначим стандартное отклонение как σ Х ) этого распределения (по аналогии с нормальным распределением ).
Ниже приведены формулы для расчета среднего и стандартного отклонения логнормального распределения .
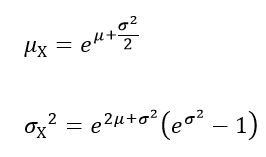
Примечание : μ и σ являются параметрами нормального распределения LN(y) и, соответственно, его средним и стандартным отклонением .
Вычисление параметров логнормального распределения через известное матожидание ожидание и дисперсию
Зная среднее и стандартное отклонение логнормального распределения можно вычислить его параметры:
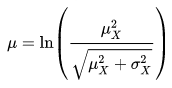
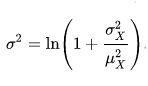
Логнормальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Логнормального распределения имеется функция ЛОГНОРМ.РАСП() , английское название - LOGNORM.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по логнормальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Логнормальное распределение имеет обозначение Ln N (μ; σ ).
Примечание : До MS EXCEL 2010 в EXCEL была функция ЛОГНОРМРАСП() , которая также позволяет вычислить кумулятивную (интегральную) функцию распределения , но не позволяет вычислить плотность вероятности . ЛОГНОРМРАСП() оставлена в MS EXCEL 2010 для совместимости. В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции распределения (использованы функции НОРМ.СТ.РАСП() и НОРМ.РАСП() .
Примечание : Для удобства написания формул в файле примера созданы Имена для параметровраспределения: μ и σ .
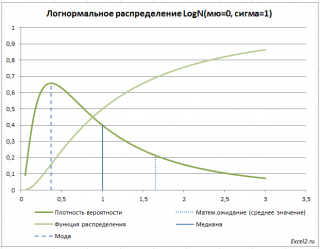
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Генерация случайных чисел
Для генерирования массива чисел, распределенных по логнормальному закону , можно использовать формулу =ЛОГНОРМ.ОБР(СЛЧИС();μ; σ ) . Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Оценку для μ (μ - параметр распределения, но не среднее ) можно сделать с использованием формулы:
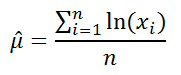
или с помощью формулы =LN(СРГЕОМ(B16:B215)) , если значения массива размещены в диапазоне B16:B215 .
Оценку для
σ
(
σ
- параметр распределения, но не
стандартное отклонение
) можно сделать с использованием формулы:
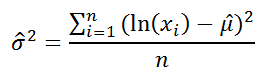
Задачи
Задача1. Время жизни лазера имеет логнормальное распределение с μ=5 и σ =1 час. Какова вероятность того, что лазер проработает >400 часов? Из определения интегральной функции распределения вычислим вероятность того, что лазер проработает меньше 400 часов. Это можно вычислить с помощью формулы (см. файл примера лист Задачи ): =ЛОГНОРМ.РАСП(400;5;1;ИСТИНА)=0,16
Тоже значение получим из формулы =НОРМ.РАСП(LN(400);5;1;ИСТИНА)
Теперь найдем вероятность того, что лазер проработает больше 400 часов: =1- ЛОГНОРМ.РАСП(400;5;1;ИСТИНА)
Задача2. Учитывая условие Задачи1, вычислить какой срок жизни будет у 99% лазеров? Если совокупность лазеров достаточно велика, то можно считать, что вопрос « Какой срок жизни x будет у 99% лазеров? » эквивалентен вопросу « Какой срок жизни x будет у случайно взятого лазера с вероятностью 99%? », т.е. вероятность, того что X> x равна 99%, где Х – случайная величина, соответствующая времени жизни лазера. Другими словами, после прошествия какого периода времени можно будет с уверенностью 99% сказать, что лазер еще работает. Здесь удобно перейти к дополнительному событию: вероятности того, что лазер сломается. Таким образом, в задаче нам необходимо вычислить значение х (время жизни), при котором 1% (1-99%) лазеров сломается, т.е. X< x .
Как и в предыдущей задаче, для формулировки условия задачи воспользуемся определением интегральной функции распределения : вероятность того, что лазер проработает меньше x часов равна 1%. Для вычисления х в MS EXCEL 2010 существует функция ЛОГНОРМ.ОБР() .
Формула =ЛОГНОРМ.ОБР(1-99%;5;1) вернет значение 14,49 часов, т.е. после 14,49 часов с начала работы 99% лазеров будут еще работать.
Примечание : пользователям более ранних версий MS EXCEL можно посоветовать для расчетов воспользоваться формулами =EXP(НОРМОБР(1-99%;5;1)) или =ЛОГНОРМОБР(1-99%;5;1) .
Задача3. Учитывая условие Задачи1, вычислить среднее и стандартное отклонение времени жизни лазера. Для заданных параметров логнормального распределения среднее значение времени жизни лазера =EXP(5+(1*1)/2)=244,69 часов, а стандартное отклонение =КОРЕНЬ((EXP(1*1)-1)*EXP(2*5+1*1))=320,75 часов.
Обратите внимание, что для логнормального распределения , как для типичного скошенного распределения, стандартное отклонение существенно больше среднего .
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
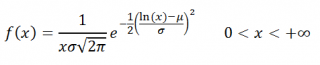
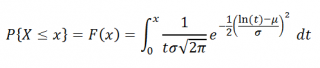
Комментарии