Комбинаторика в EXCEL

Обзорная статья, в которой приведены основные функции MS EXCEL для вычисления количества перестановок, сочетаний и размещений. Рассмотрены варианты комбинаций без повторений и с повторениями (выборка с возвращением).

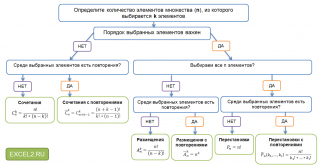
Чтобы не запутаться в терминологии комбинаторики, в ее формулах и обозначениях, предлагаем воспользоваться нижеследующей диаграммой:

В разделе Комбинаторика вы можете найти статьи, касающиеся теории:

Перестановки без повторений: Комбинаторика в MS EXCEL

Перестановки с повторениями: Комбинаторика в MS EXCEL

Размещения без повторений: Комбинаторика в MS EXCEL

Размещения с повторениями: Комбинаторика в MS EXCEL

Сочетания без повторений: Комбинаторика в MS EXCEL

Сочетания с повторениями: Комбинаторика в MS EXCEL

Комбинации элементов из нескольких множеств: Комбинаторика в MS EXCEL

Для вычисления количества перестановок в MS EXCEL имеется функция ФАКТР(n), также можно использовать функцию ПЕРЕСТ(n;n) с одинаковыми аргументами, равными количеству элементов множества. Для вычисления количества размещений имеется функция ПЕРЕСТ(n;k), для сочетаний используйте функцию ЧИСЛКОМБ(n;k). Подробности применения этих функций см. в вышеуказанных статьях.