Комбинации элементов из нескольких множеств: Комбинаторика в EXCEL

Пусть имеется несколько множеств — {A1, A2, A3, А4 ...}, {B1, B2, B3, ...}, {C1, C2, ...}, количество элементов в которых может быть различно. Требуется составить все возможные комбинации элементов этих множеств таким образом, чтобы в комбинации присутствовал только один элемент из каждого множества: (A1, B1, C1), (A1, B2, C1), (A1, B2, C2), … Также подсчитаем в MS EXCEL количество таких комбинаций.

Начнем со множеств, состоящих из последовательностей целых чисел без повторов с шагом =1. Например, {1; 2; 3; 4} или {-1; 0; 1; 2; 3}. В файле примера создана форма для 4-х множеств, состоящих из 6 элементов (максимум).

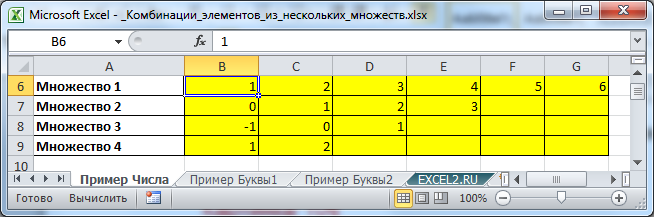
В пределах одного множества все элементы должны быть разными, а элементы, принадлежащие разным множествам, могут повторяться. Количество элементов во множествах может быть различным.

Число различных комбинаций, содержащих по одному элементу из каждого множества, равно произведению количеств элементов каждого множества. Например, как следует из картинки выше, число комбинаций =6*4*3*2=144.

С помощью простых формул можно найти все эти 144 комбинации (см. файл примера лист Пример Числа )

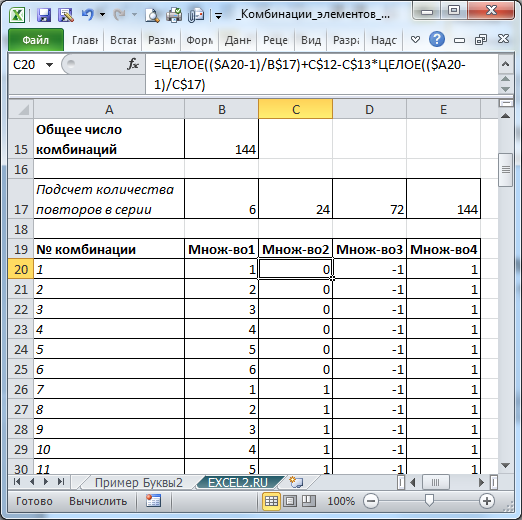
Изменяя количество элементов во множествах, будут автоматически изменяться число комбинаций и сами комбинации (необходимо следить, чтобы количество строк с формулами было достаточным для отображения всех комбинаций).

При необходимости, в файле примера можно легко увеличить как количество множеств, так и количество элементов в каждом из множеств. Для этого нужно скопировать формулы в ячейки справа.

Примечание : Если все множества идентичны (состоят из одинаковых элементов), то задача сводится к Размещению с повторениями . Действительно, пусть в каждом из k множеств по n элементов. Произведение количеств элементов (n) k раз, равно n^k, что равно количеству Размещений с повторениями.

Множества, состоящие из букв (символов)

Если необходимо составить комбинации нечисловых элементов, например, взяв множества {A, Б, В}; {Й, Ц, А}, то вышеуказанный подход также можно использовать. Для этого произвольным образом нужно сопоставить буквам последовательные числовые значения.

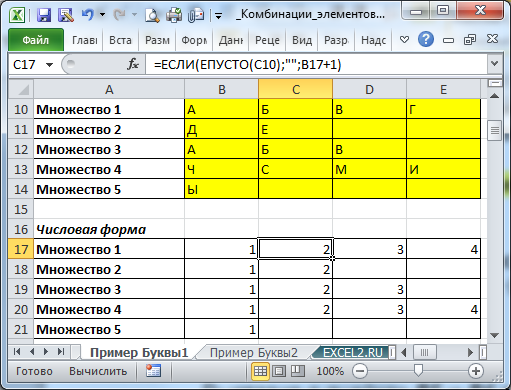
После того, как все комбинации для числовых эквивалентов будут построены, необходимо сделать обратное преобразование: каждому числу сопоставить соответствующую букву (см. лист Пример Буквы1 ).

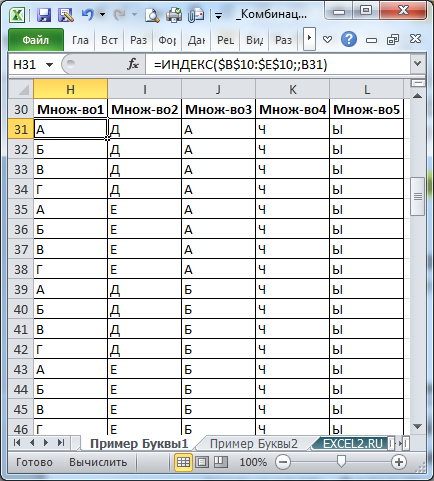
Примечание : Существует и прямой подход, изложенный на сайте ]]> https://sites.google.com/site/e90e50fx/home/combinatorics-using-excel-formulas-and-examples#TOC-Combine-elements-of-different-sets ]]> (см. лист в файле примера Пример Буквы2 ). Правда, для этого необходимо создать зубодробительную формулу массива .