Перестановки с повторениями: Комбинаторика в EXCEL

Подсчитаем в MS EXCEL количество перестановок с повторениями из n элементов. С помощью формул выведем на лист все варианты таких перестановок (английский перевод термина: permutations of multisets).

Напомним, что Перестановкой множества из n элементов называется расположение элементов в определенном порядке. Число Перестановок n элементов равно n! (факториал) (см. статью Перестановки без повторений: Комбинаторика в MS EXCEL ). Для вычисления факториала в MS EXCEL есть специальная функция ФАКТР() .

Обычно, перестановки рассматривают для множества с неповторяющимися элементами, например для {1; 2; 3; 4; 5; 6}. Всего перестановок в этом случае 6!=720. Вариантами перестановок являются  {1; 2; 3; 4; 5; 6};  {2; 1; 3; 4; 5; 6};  {5; 2; 3; 4; 1; 6};  {3; 2; 1; 5; 4; 6} и т.д., всего 720.

Если элементы множества повторяются, например, {1; 1; 1; 2; 4; 4}, то количество перестановок равно 6!/(3!1!2!) (6 – это общее количество элементов множества, 3 – это количество повторов числа 1; 1 – т.к. число 2 в единственном экземпляре, а 2 – это 2 повтора числа 4). Т.е. всего 60 перестановок, что существенно меньше, чем для того же количества элементов без повторений.

Для небольшого количества элементов в EXCEL возможно отобразить все варианты комбинаций с помощью всего нескольких формул. Например, для множества из 7 элементов {1; 1; 2; 2; 3; 3; 3} вариантов перестановки будет всего 210.

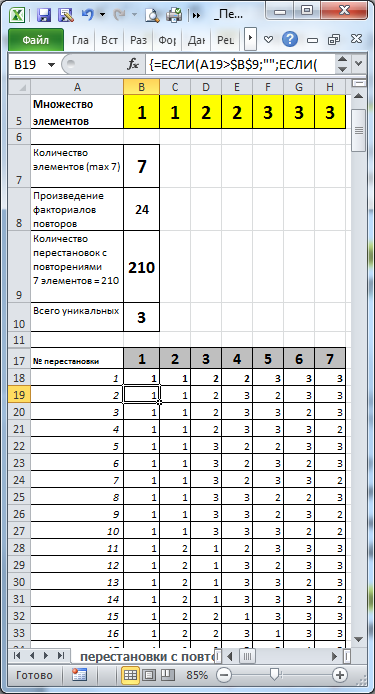
В файле примера организован вывод всех Перестановок с повторениями для заданного множества (максимум 7 элементов) и подсчет количества таких перестановок.

Также в файле примера даны рекомендации как увеличить количество элементов множества и на отдельном листе приведен пример увеличения множества с 7 до 8 элементов (указано какие столбцы добавлять и какие формулы копировать). Написания или изменения формул не требуется.

Перед увеличением количества элементов вычислите количество комбинаций, т.к. количество комбинаций очень быстро растет при росте размера множества элементов. Так для 15 элементов количество комбинаций превышает 1 триллион (если повторов нет). Фактически в книге EXCEL пределом будет размещение нескольких десятков тысяч комбинаций, т.к. в файле использованы ресурсоемкие формулы массива, вычисление которых требует времени.

Если множество состоит из букв, например, слово MISSISSIPPI, то можно подсчитать количество анаграмм (слов, состоящих из тех же букв): 11!/(1!4!4!2!) (11 – это общее количество букв, 1 – одна буква M; 4 – это 4 повтора буквы I, а вторая 4 – это 4 повтора буквы S, 2 – это 4 повтора буквы P).

Примечание : О Размещениях можно прочитать в статье Размещения без повторений: Комбинаторика в MS EXCEL , а о Сочетаниях в статье Сочетания без повторений: Комбинаторика в MS EXCEL .