Сочетания с повторениями: Комбинаторика в EXCEL

Подсчитаем в MS EXCEL количество Сочетаний с повторениями из n по k (выборка с возвращением). Также с помощью формул выведем на лист соответствующие варианты Сочетаний (английский перевод термина: combinations with repetition).

Сочетания с повторениями (выборка с возвращением) — это Сочетание n объектов по k в предположении, что каждый объект может участвовать в сочетании несколько раз .

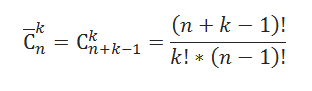
Примечание : О Сочетаниях без повторений (без возвращения элементов) можно прочитать в статье Сочетания без повторений: Комбинаторика в MS EXCEL

Например, из множества содержащего 3 (n) различных элемента ( a, b, c ) можно сформировать 6 =ФАКТР(3+2-1) / (ФАКТР (3-1) * ФАКТР (2)) упорядоченных наборов по 2 (k) элемента: аа, ab, ac, bb, bc, сс . В отличие от Сочетаний без повторений наборы аа, bb и сс допустимы. В отличие от Размещений наборы ac и ca считаются одинаковыми (порядок не важен).

В отличие от Сочетаний без повторений , k может быть меньше или больше n. Например, из множества содержащего 2 (n) различных элемента ( a, b ) можно сформировать 4 =ФАКТР(2+3-1) / (ФАКТР (2-1) * ФАКТР (3)) упорядоченных наборов по 3 (k) элемента (т.е. 4 сочетания с повторениями из 2 по 3): ааa, аab, abb, bbb.

В файле примера MS EXCEL приведен подсчет количества Сочетаний с повторениями и созданы формулы для вывода всех Сочетаний для заданных n и k.

Задавая с помощью элементов управления Счетчик количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания с повторениями.

Задача

В магазине платки 4-х цветов продаются вперемешку в огромной корзине. Женщина не может определиться с выбором, и поэтому решается довериться случаю – выбрать не глядя 3 платка. Определить число различных вариантов покупки 3-х платков.

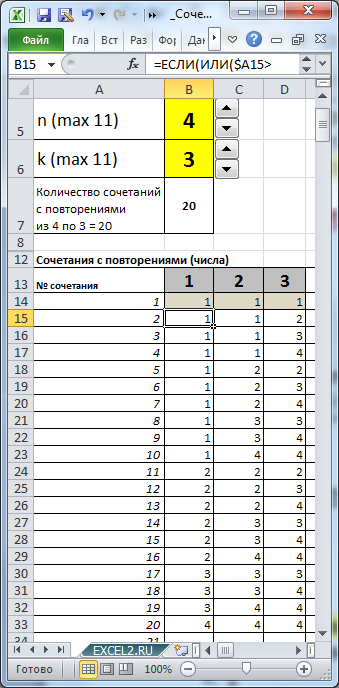
Так как не важно, в какой последовательности женщина будет выбирать платки, то нам нужно определить число Сочетаний с повторениями покупки 3-х платков 4-х возможных цветов. Т.е. n=4, а k=3. Оказывается, что таких вариантов =(4+3-1)!/(4-1)!/3! равно 20.

Воспользуемся файлом примера , чтобы убедиться, что мы решили задачу правильно.

По аналогии с решением задачи в статье Размещения без повторений сопоставим произвольным образом 4-м различным цветам числовые значения: 1; 2; 3; 4.

Выставив в ячейках В5 и В6 значения 4 и 3 соответственно, определим все варианты размещений.

Примечание : О Перестановках можно прочитать в статье Перестановки без повторений: Комбинаторика в MS EXCEL , а о Размещениях в статье Размещения без повторений: Комбинаторика в MS EXCEL .