Размещения без повторений: Комбинаторика в EXCEL

Подсчитаем в MS EXCEL количество Размещений из n по k и с помощью формул выведем на лист соответствующие варианты размещений (английский перевод термина: partial permutation или sequence without repetition).

Размещением (partial permutation) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.

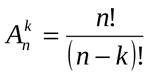
Например, из множества содержащего 3 (n) различных элемента ( a, b, c ) можно сформировать 6 упорядоченных наборов по 2 (k) различных элемента (т.е. 6 размещений из 3 по 2): ab, ac, ba, bc, ca, cb . В отличие от Размещений с повторениями повторы элементов в наборах не допускаются, т.е. наборы аа , bb и сс не допустимы. В отличие от Сочетаний наборы ac и ca считаются различными (важен порядок). Очевидно, что k =< n , т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются).

Примечание : О Размещениях с повторениями (с возвращением элементов) можно прочитать в статье Размещения c повторениями: Комбинаторика в MS EXCEL . Для вычисления количества Размещений в MS EXCEL имеется специальная функция ПЕРЕСТ() . Чтобы подсчитать количество Размещений из 3 (n) по 2 (k) нужно записать формулу =ПЕРЕСТ(3;2) Примечание : Название функции ПЕРЕСТ() не соответствует общепринятой терминологии в комбинаторике на русском языке, по сути подсчитывая количество Размещений (хотя, справедливости ради, нужно отметить, что Перестановки она тоже считает при n=k). Причиной расхождения, вероятно, является калька с английского названия функции PERMUT(), т.е. permutation (перестановка). Примечание : Если k=n, то количество Размещений из n по n равно числу Перестановок из n элементов, т.е. n!=ФАКТР(n)=ПЕРЕСТ(n;n).

В файле примера MS EXCEL приведен подсчет количества Размещений с помощью функции =ПЕРЕСТ(n;k) и альтернативной формулы =ФАКТР(n)/ФАКТР(n-k).

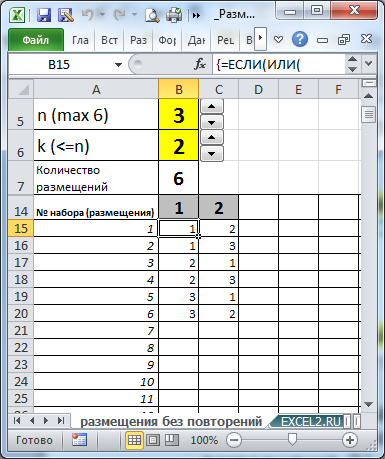
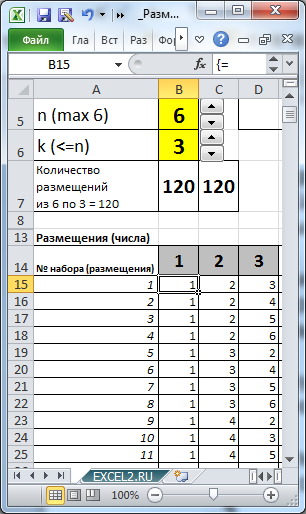
Кроме того, в файле примера создана универсальная формула для вывода всех Размещений для заданных n и k. Задавая с помощью элементов управления Счетчик количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формулы массива можно вывести все Размещения. Например, для n=3 (соответствующее множество равно {1; 2; 3}) и к=2 можно сформировать 6 пар размещений.

Задача

6 машин разных марок участвуют в гонках на выживание: LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo. Определить число возможных вариантов распределения 3-х призовых мест между участниками.

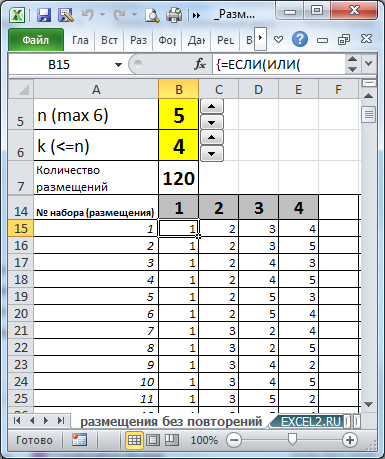
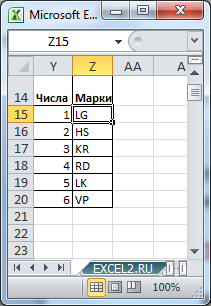
Нам нужно определить число размещений 6 машин на 3-х призовых местах (понятно, что порядок размещения машин на призовых местах важен). Т.е. n=6, а k=3. Оказывается, что таких вариантов =ПЕРЕСТ(6;3) равно 120. Воспользуемся файлом примера , чтобы наглядно убедиться, что мы решили задачу правильно. Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …

Выставив в ячейках В5 и В6 значения 6 и 3, определим все варианты размещений машин на призовых местах.

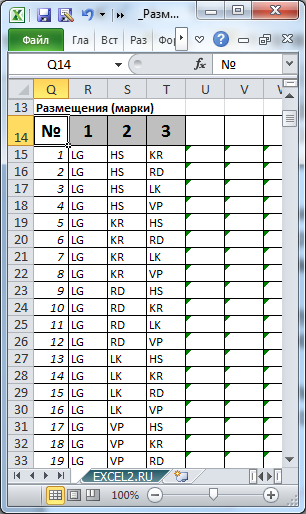
В столбцах Q:T числовым значениям сопоставлены марки машин.

Примечание : О Перестановках можно прочитать в статье Перестановки без повторений: Комбинаторика в MS EXCEL , а о Сочетаниях в статье Сочетания без повторений: Комбинаторика в MS EXCEL . Примечание : В данной статье рассмотрена выборка элементов из одного массива, в котором содержится n элементов. В статье Комбинации элементов из нескольких множеств составлены все возможные комбинации элементов таким образом, чтобы в комбинации присутствовал один и только один элемент из каждого множества.