Доверительный интервал для разницы средних значений 2-х распределений (дисперсии неизвестны, но равны) в EXCEL
9 декабря 2016 г.
- Группы статей
- Статистический вывод
Построим доверительный интервал для разницы средних значений 2-х распределений в случае неизвестных, но равных дисперсий.
Имеется две независимых случайных величины. Эти случайные величины имеют распределения с неизвестными средними значениями μ 1 и μ 2 . Дисперсии этих распределений неизвестны, но равны между собой ( дисперсию обозначим σ 2 ). Из этих распределений получены две выборки размером n 1 и n 2 (в общем случае размеры выборок также могут быть не равны между собой).
Формулировка задачи. Нас интересует разница средних значений этих распределений: μ 1 - μ 2 . Мы делаем предположение, что эта разница равна Δ 0 , т.е. Δ 0 = μ 1 - μ 2 . От нас требуется дать точечную оценку для Δ 0 и построить для нее двухсторонний доверительный интервал .
СОВЕТ : Для построения Доверительного интервала нам потребуется знание следующих понятий:
- дисперсия и стандартное отклонение ,
- выборочное распределение статистики ,
- уровень доверия/ уровень значимости ,
- нормальное распределение ,
- t-распределение Стьюдента и его квантили .
Примечание : Если заданное значение Δ 0 равно 0, то мы предполагаем, что средние этих распределений совпадают.
Примечание : Процедура построения доверительного интервала более подробно изложена в статье Доверительный интервал для оценки разницы средних значений 2-х распределений (дисперсии известны) .
Точечной оценкой для μ 1 - μ 2 является разница между средними значениями, вычисленными на основании выборок из этих (независимых) распределений, т.е. Хср 1 - Хср 2 .
На основании свойств дисперсии имеем, что VAR(Хср 1 -Хср 2 )= VAR(Хср 1 )+ VAR(Хср 2 ) = σ 1 2 /n 1 + σ 2 2 /n 2 =σ 2 (1/n 1 +1/n 2 ).
Следовательно , статистика Хср 1 -Хср 2 имеет нормальное распределение N(μ 1 - μ 2 ; σ 2 (1/n 1 +1/n 2 ).
Т.к. дисперсия σ 2 нам неизвестна, то вместо нее используем ее оценку: так называемую объединенную оценку дисперсии s p 2 (pooled estimate of variance).
В случае неизвестной дисперсии, статистика Хср 1 -Хср 2 имеет t-распределение с n 1 +n 2 –2 степенями свободы (см. статью про построение доверительного интервала для среднего в случае неизвестной дисперсии ).
По аналогии с доверительным интервалом для среднего (дисперсия неизвестна) запишем выражение для вычисления двухстороннего доверительного интервала для μ 1 - μ 2 , заменив σ 2 на ее оценку s p 2 :
где t α/2, n1+n2-2 – верхний α/2-квантиль t -распределения с n 1 +n 2 –2 степенями свободы .
Примечание : Верхний α/2 -квантиль - это такое значение случайной величины t n1+n2–2 , что P ( t n1+n2–2 >=t α/2, n1+n2–2 )= α /2. Подробнее о квантилях распределений см. статью Квантили распределений MS EXCEL .
Чтобы в MS EXCEL вычислить значение t α /2, n1+n2–2 для различных уровней значимости (10%; 5%; 1%) и степеней свободы можно использовать несколько формул: =СТЬЮДЕНТ.ОБР.2Х(α; n1+n2–2) =СТЬЮДЕНТ.ОБР(1- α /2; n1+n2–2) =-СТЬЮДЕНТ.ОБР( α /2; n1+n2–2) =СТЬЮДРАСПОБР( α ; n1+n2–2)
Примечание : Подробнее про функции MS EXCEL, связанные с t - распределением см. статью t-распределение .
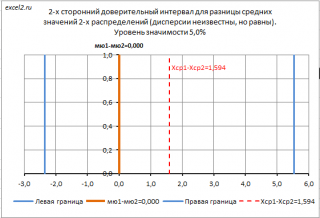
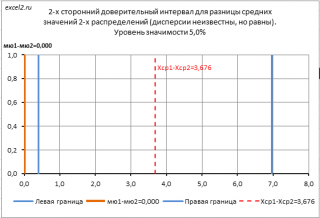
В файле примера на листе Двухсторонний приведен пример построения двухстороннего доверительного интервала .
Доверительный интервал построен относительно Хср 1 - Хср 2 . Если гипотетическое значение разности μ 1 - μ 2 не попадает в интервал, то это является основанием для отклонения соответствующей нулевой гипотезы . Подробнее о проверке гипотез о разнице средних значений 2-х распределений (дисперсии неизвестны, но равны) см. статью Двухвыборочный t-тест с одинаковыми дисперсиями в MS EXCEL .
В файле примера на листе Односторонний также приведены расчеты границ односторонних доверительных интервалов .
Примечание : Распределения, из которых берутся выборки , не обязательно являются нормальными . Однако, требуется чтобы выполнялись условия применимости Центральной предельной теоремы . Если размеры выборок меньше 30, то для справедливости сделанных здесь выводов, необходимо, чтобы выборки были сделаны из нормального распределения .
СОВЕТ : О построении других доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .
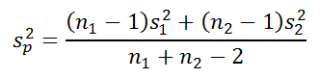
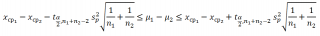
Комментарии