Взаимосвязь некоторых распределений в EXCEL
6 ноября 2016 г.
- Группы статей
- Комбинаторика
- Распределения вероятностей
Рассмотрим взаимосвязь Биномиального распределения, распределения Пуассона, Нормального распределения и Гипергеометрического распределения. Определим условия, когда возможна аппроксимация одного распределения другим, приведем примеры и графики.
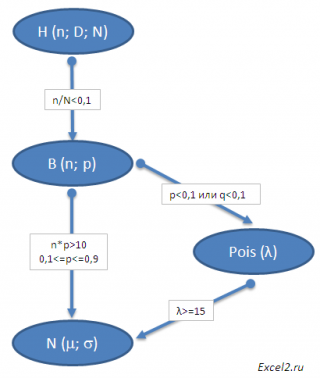
Схема взаимосвязи 4-х распределений случайных величин выглядит так:
- Биномиальное распределение B(n;p),
- Распределение Пуассона Pois(λ),
- Нормальное распределение N(μ;σ) и
- Гипергеометрическое распределение H(n;D;N)
Формулы приближенного вычисления разрабатывались для упрощения и ускорения вычислений в условиях отсутствия или дороговизны времени вычислительных машин. Учитывая современные возможности компьютеров, аппроксимация для этих целей сейчас стала бессмысленна. Однако, примеры, рассмотренные ниже, полезны для понимания условий применения того или иного распределения при решении реальных практических задач и понимания взаимосвязи различных распределений между собой.
Аппроксимация Гипергеометрического распределения Биноминальным распределением
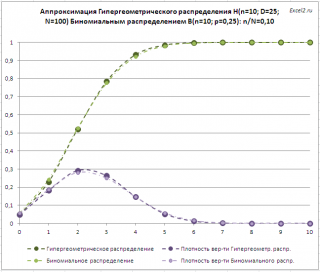
В случае, когда размер совокупности N Гипергеометрического распределения гораздо больше размера выборки n (т.е., N >> n или n/N<<1), то данное распределение хорошо аппроксимируется Биномиальным распределением с параметрами n (количество испытаний) и p = D / N (вероятность успеха в одном испытании). Как видно на картинке ниже, уже при n/N=0,1 Гипергеометрическое распределение достаточно хорошо аппроксимируется Биномиальным.
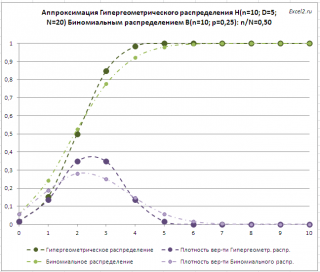
При n/N=0,5 – оба распределения существенно отличаются (см. файл примера, лист Гипергеом-Биномин ):
Почему же при N>>n имеет место хорошая аппроксимация? Дело в том, что в случае Гипергеометрического распределения выборка производится без возвращения , т.е., результат каждого последующего испытания зависит от результатов предыдущих испытаний, что является нарушением условия применимости Биномиального распределения . По мере уменьшения отношения n/N предыдущие испытания все меньше и меньше влияют на исход последующих, тем самым обеспечивая выполнение условий эксперимента по Схеме Бернулли , лежащей в основе Биномиального распределения , что в свою очередь приводит к совпадению результатов этих двух распределений.
Связь Распределения Пуассона и Биномиального распределения
Распределение Пуассона с параметром λ( лямбда) является предельным случаем Биномиального распределения , при условии, если:
- параметр n Биномиального распределения стремится к бесконечности;
- вероятность успеха p стремится к 0;
- произведение n * p =λ достаточно мало и постоянно.
Строгое доказательство этого утверждения называется теоремой Пуассона , а приближенная формула – формулой Пуассона .
Примечание : Вывод формулы Пуассона основан на известном пределе
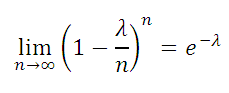
Можно сформулировать условия, когда приближение распределением Пуассона работает хорошо:
- p <0,1 (чем меньше p и больше n , тем приближение точнее);
- p >0,9 (учитывая, что q =1- p , вычисления в этом случае необходимо производить через q (а х нужно заменить на n - x ). Следовательно, чем меньше q и больше n , тем приближение точнее).
Примечание : Если 0,1<=p<=0,9, а n*p>10, то Биномиальное распределение можно аппроксимировать Нормальным распределением . Подробнее, см. раздел Аппроксимация Биномиального распределения Нормальным распределением .
Для пояснения связи этих двух распределений рассмотрим задачу.
Задача
Известно, что среднее количество звонков, поступающих на телефонную станцию в течение 1 часа, равно 50. Необходимо произвести расчет вероятности количества вызовов, поступивших на станцию за 1 час.
Т.к. звонки делаются независимо, а средняя частота звонков постоянна, то вероятность количества звонков, поступивших на станцию за 1 час, можно смоделировать распределением Пуассона с параметром λ=50.
Теперь взглянем на ситуацию не с позиции телефонной станции, а с позиции поступления отдельных звонков, и построим модель на основе Биномиального распределения с параметрами n и p .
В основе Биномиального распределения лежит Схема Бернулли . Испытание в нашем случае будет состоять из регистрации факта поступления 1 звонка на станцию за определенный период времени. Напомним, что для применения Схемы Бернулли должны быть выполнены следующие 3 условия:
- Каждое испытание должно иметь только два исхода , условно называемых «успехом» и «неудачей». Для нашего случая – поступил звонок или нет;
- Результат каждого эксперимента не должен зависеть от результатов предыдущих экспериментов (независимость испытаний). Для нашего случая это обеспечивается предположением о независимости звонков от разных абонентов (звонят не сговариваясь).
- Вероятность успеха p должна быть постоянной для всех испытаний. В нашем случае вероятность регистрации звонка не зависит от того когда он был сделан: в начале периода наблюдения (часа) или в конце.
Предположим, что сначала решили, что в течение часа будет проведено 100 наблюдений (n=100). Т.е. каждые 36 секунд (1час= 3600сек) будет фиксироваться факт поступления звонка, причем звонок должен быть единственным за период наблюдения (требования условия 1 ). Но, это условие может быть и не выполнено, т.к. в течение 36 секунд может поступить 2 и более звонка. Это следует, из того что вероятность p поступления 1 звонка в течение данного периода наблюдения достаточно высока и равна 0,5=50%: в час поступает 50 звонков, т.е. в среднем 1 звонок за 3600сек/50=72 сек. Кроме того, параметр распределения Пуассона λ = n * p , следовательно p =50/100=0,5 .
Поэтому, чтобы соблюсти условие 1 применимости Биномиального распределения , необходимо сократить период наблюдения, увеличив n, тем самым исключив возможность регистрации за период наблюдения более 1 звонка.
Увеличим размер выборки n до 1000. Теперь факт поступления звонка будет фиксироваться каждые 3,6 сек=(1час=3600сек)/1000. В этом случае вероятность «успеха» p в одном испытании по Схеме Бернулли будет равна 50 звонков /1000 интервалов=0,05 . Теперь мы выполнили все 3 условия необходимые для применения приближения Биномиального распределения распределением Пуассона (см. начало статьи) .
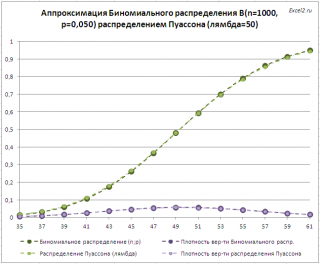
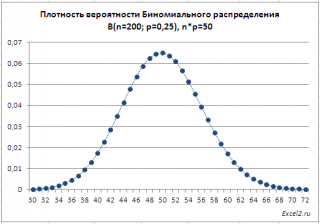
При n=1000 обе модели ( распределение Пуассона и Биномиальное распределение ) должны давать одинаковый результат. Следовательно, формулы =БИНОМ.РАСП(x;n;p;ИСТИНА) и =ПУАССОН.РАСП(x;n*p;ИСТИНА) должны возвращать примерно одинаковые значения для одних и тех же х . Это видно на картинке ниже (см. файл примера лист Биномин-Пуассон ).
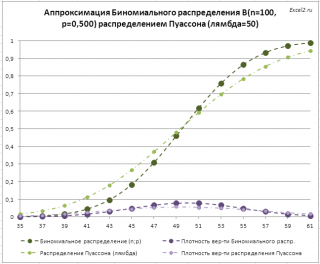
По мере уменьшения размера выборки n (при этом будет пропорционально увеличиваться вероятность p , т.к. будет расти интервал наблюдения за поступившими звонками), то приближение будет все менее точным (из-за нарушения условия 1 применимости Биномиального распределения ).
Например, при n=100, оба распределения будут существенно отличаться (для удобства изменения интервала в файле примера использован элемент управления Счетчик ).
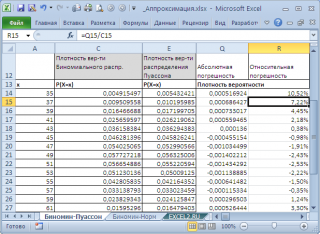
О точности приближения. Как было показано выше, из формулы Пуассона следует, что при увеличении n разность между величинами, вычисленными по формулам ПУАССОН.РАСП() и БИНОМ.РАСП() стремится к нулю. Однако, следует учитывать, что формула Пуассона гарантирует только малую абсолютную погрешность, а относительная погрешность, может быть сколь угодно большой.
Например, для n=1000 и p=0,05 (λ=50) относительная погрешность при вычислении плотности вероятности составляет несколько процентов (см. файл примера лист Биномин-Пуассон ).
При уменьшении n (и, соответственно, увеличении p ), относительная погрешность существенно возрастает и может стать неприемлемой.
Аппроксимация Биномиального распределения Нормальным распределением
Если параметры Биномиального распределения B(n;p) находятся в пределах 0,1<=p<=0,9 и n*p>10, то Биномиальное распределение можно аппроксимировать Нормальным распределением.
При n*p>10 форма графика плотности вероятности Биномиального распределения близка к колоколообразной форме Нормального распределения .
Напомним, что математическое ожидание (среднее) Биномиального распределения равно n*p, а дисперсия = n*p*q. Нормальное распределение с параметрами:μ= n*p,σ =КОРЕНЬ(n*p*q) хорошо аппроксимирует соответствующее Биномиальное распределение .
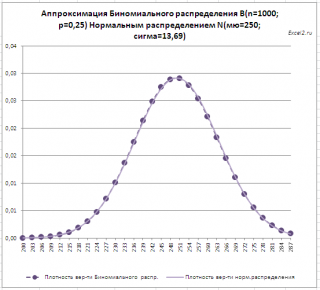
Как видно из рисунка выше, формулы =БИНОМ.РАСП(x;n;p;ЛОЖЬ) и =НОРМ.РАСП(х;n*p;КОРЕНЬ(n*p*(1-p));ЛОЖЬ)
возвращают примерно одинаковые результаты: относительная погрешность составляет примерно 1% (см. файл примера лист Биномин-Норм, столбец S ).
Приложение : Строгое математическое доказательство, обосновывающее возможность этого приближения, называется локальной теоремой Муавра-Лапласа, которая является следствием более общей Центральной предельной теоремы .
Приближение также можно осуществить через интегральную функцию нормального распределения , введя так называемую поправку на дискретность, вследствие того, что аппроксимируемое Биномиальное распределение является дискретным , а Нормальное распределение – непрерывным распределением . Поправка заключается в том, что для оценки вероятности биномиальной случайной величины принять некое значение х, вычисляется вероятность случайной величины, распределенной по соответствующему нормальному закону , принять значение в диапазоне от x-0,5 до x+0,5. В файле примера это реализовано с помощью формулы: =НОРМ.РАСП(x+0,5;n*p;КОРЕНЬ(n*p*(1-p));ИСТИНА)- НОРМ.РАСП(x-0,5;n*p;КОРЕНЬ(n*p*(1-p));ИСТИНА)
Результаты вычислений по обеим формулам (через плотность вероятности и интегральную) практически совпадают: для μ=250 относительная разница составляет доли процента.
Изначально формулы приближенного вычисления разрабатывались для упрощения вычислений. Хотя в современных условиях это уже не актуально, использование аппроксимирующего распределения, в некоторых случаях может упростить ход решения задачи. Поясним на примере.
Задача . Производственный процесс изготавливает десятки тысяч микросхем в день. В среднем, 10% микросхем – бракованные (доля дефектных равна 0,1). Регулярно, контролер качества отбирает партию определенного размера и тестирует микросхемы. Нужно определить, размер партии n , при котором наблюденная частота f = x брак / n с вероятностью 0,95 отличается от доли дефектных изделий 0,1 не более чем на 0,02.
Решение1 . Вероятность обнаружить в контрольной партии размера n определенное число х бракованных микросхем при доли дефектных p=0,1 соответствует модели Биномиального распределения .
По условиям задачи вероятность отклонения частоты f в обе стороны от ожидаемого значения 0,1 должна быть меньше 5% (1-0,95). Вероятность отклонения частоты f только в одну сторону, например в сторону превышения, должна быть меньше 5%/2=2,5%. Эта вероятность является альфа-риском (риском отклонить гипотезу, что оцениваемая доля бракованных p не больше заданного нами порогового значения). Поэтому, мы можем оценить наибольшее значение x, при котором с вероятностью 0,975 диапазон отклонения f от p еще не будет превышать 0,02. Для этого расчета в MS EXCEL можно использовать функцию БИНОМ.ОБР() или КРИТБИНОМ() для MS EXСEL 2007 и более ранних версий.
В качестве аргументов функции БИНОМ.ОБР() нужно указать размер выборки n, вероятность «успеха» p (т.е. обнаружения брака) и альфа-риск . Для расчетов в файле примера на листе Биномин-Норм создана форма, в которой, с использованием инструмента Подбор параметра, можно подобрать размер выборки n. В результате расчетов получим, что выборка должна быть не меньше 875 микросхем.
Решение2 . Учитывая, что для данных значений n и p возможно использовать приближение нормальным распределением с параметрами μ=n*p и σ =КОРЕНЬ(n*p*(1-p)) , решим задачу другим способом.
Ожидаемое количество бракованных изделий в партии размера n равно n*p. В соответствии с условиями задачи, количество бракованных изделий должно лежать в пределах [n*p-0,02*n; n*p+0,02*n] с вероятностью 95%. Воспользовавшись нормальным распределением , вычислим вероятность, того что количество бракованных микросхем будет находиться в этом диапазоне. Это можно сделать с помощью выражения: =НОРМ.РАСП(n*p+0,02*n; n*p; КОРЕНЬ(n*p*(1-p)); ИСТИНА) – НОРМ.РАСП(n*p-0,02*n; n*p; КОРЕНЬ(n*p*(1-p)); ИСТИНА)
Это выражение, при определенном n, должно равняться заданной вероятности 95%. Подбор n также сделаем с использованием инструмента Подбор параметра (в параметрах MS EXCEL установите количество итераций=1000, а точность 0,0001 или точнее). Найденное решение будет равно 864, что близко к результату, полученному с использованием Биномиального распределения . Причем ход решения даже прозрачней, чем в первом варианте решения.
Примечание : Решение задачи близко по сути с определением доверительного интервала .
Аппроксимация распределения Пуассона Нормальным распределением
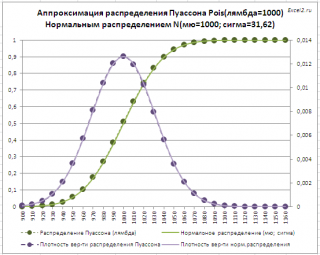
При значениях λ >15 , Распределение Пуассона хорошо аппроксимируется Нормальным распределением со следующими параметрами: μ=λ , σ 2 =λ .
Для λ =1000 относительная погрешность составляет менее 1%. Расчеты приведены в файле примера на листе Пуассон-Норм .
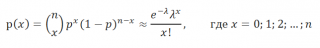
Комментарии