Гипергеометрическое распределение. Дискретные распределения в EXCEL
7 ноября 2016 г.
- Группы статей
- Распределения вероятностей
Рассмотрим Гипергеометрическое распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ГИПЕРГЕОМ.РАСП() построим графики функции распределения и плотности вероятности. Приведем пример аппроксимации гипергеометрического распределения биномиальным.
Определение . Рассмотрим совокупность, состоящую из N элементов. Известно, что элементы в этой совокупности принадлежат разным классам, например, часть элементов зеленого цвета, другая часть – красного, третья – черного и т.д. Нас интересует только определенный класс элементов, например, только зеленые элементы. Известно, что в нашей совокупности содержится D элементов интересующего нас класса (D<=N), т.е. D зеленых элементов.
Пусть из совокупности делается выборка без возвращения , состоящая из n элементов. Гипергеометрическое распределение (англ. Hypergeometric distribution ) моделирует вероятность получить x «удачных» наблюдений в выборке . В нашем случае «удачным» наблюдением является наличие в нашей выборке элементов зеленого элемента.
Другими словами, х является случайной величиной распределенной по гипергеометрическому закону . Плотность Гипергеометрического распределения задается следующей формулой:
N — размер всей совокупности, D — число элементов, интересующего нас класса (общее число_успехов_в_совокупности), n — размер_выборки, x — число_успехов_в_выборке.
Примечание
: Запись
![]() означает количество
Сочетаний
из N элементов по n. Для сочетаний также используют эквивалентную запись
означает количество
Сочетаний
из N элементов по n. Для сочетаний также используют эквивалентную запись
![]() . Подробнее о
сочетаниях
см. статью
Сочетания без повторений: Комбинаторика в MS EXCEL
.
. Подробнее о
сочетаниях
см. статью
Сочетания без повторений: Комбинаторика в MS EXCEL
.
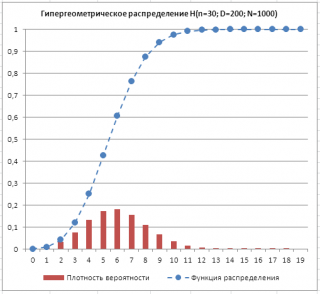
Примечание : На диаграмме значения функции распределения соединены пунктирной линией для наглядности ( функция распределения определена только для целых х).
Примечание : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
Гипергеометрическое распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Гипергеометрического распределения имеется функция ГИПЕРГЕОМ.РАСП() , английское название - HYPGEOM.DIST(), которая позволяет вычислить не только вероятность того, что в выборке будет х нужных нам элементов ( функцию плотности вероятности ), но и интегральную функцию распределения (вероятность того, что в выборке будет не меньше x нужных нам элементов).
До MS EXCEL 2010 в EXCEL была только функция ГИПЕРГЕОМЕТ() , которая позволяла вычислить только плотность вероятности. ГИПЕРГЕОМЕТ() оставлена в MS EXCEL 2010 только для совместимости. Для пользователей MS EXCEL 2007 и более ранних – в файле примера приведена формула для расчета интегральной функции распределения на основе функции ГИПЕРГЕОМЕТ() .
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Гипергеометрическое распределение имеет обозначение H ( n ; D ; N ) .
Примечание : Для построения интегральной функции распределения идеально подходит диаграмма типа График , для плотности распределения – Гистограмма с группировкой . Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
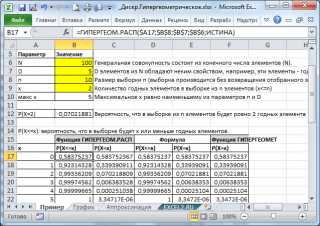
В файле примера приведены различные расчеты вероятности:
Как видно на картинке выше, для расчета предполагается, что:
- совокупность, из которой делается выборка, состоит из 100 элементов (N, четвертый аргумент функции ГИПЕРГЕОМ.РАСП() ).
- Всего в этой совокупности содержится 5 элементов интересующего нас класса, например, «годных» элементов (D, третий аргумент функции).
- Чтобы вычислить вероятность, того что в выборке из 10 элементов (n, второй аргумент функции) будет 2 элемента из интересующего нас класса (первый аргумент функции), нужно записать формулу: =ГИПЕРГЕОМ.РАСП(2;10;5;100;ЛОЖЬ)
- Последний, пятый элемент, установлен =ЛОЖЬ, т.е. возвращается значение функции плотности распределения .
Если значение пятого аргумента =ИСТИНА, то функция ГИПЕРГЕОМ.РАСП() возвращает значение интегральной функции распределения или просто Функцию распределения . В этом случае можно рассчитать вероятность того, что в выборке количество «годных элементов» будет из определенного диапазона, например, 2 или меньше (включая 0). Для этого нужно записать формулу: =ГИПЕРГЕОМ.РАСП(2;10;5;100;ИСТИНА)
Примечание : При нецелом значении х, дробная часть отбрасывается . Например, следующие формулы вернут одно и тоже значение:
ГИПЕРГЕОМ.РАСП( 2 ;10;5;100;ИСТИНА) = ГИПЕРГЕОМ.РАСП( 2,9 ;10;5;100;ИСТИНА)
Чтобы вычислить вероятность того, что в выборке окажется 1, 2 или 3 «годных» элемента нужно записать выражение: =ГИПЕРГЕОМ.РАСП(3;10;5;100;ИСТИНА)- ГИПЕРГЕОМ.РАСП(0;10;5;100;ИСТИНА) или
=ГИПЕРГЕОМ.РАСП(1;10;5;100;ЛОЖЬ)+ +ГИПЕРГЕОМ.РАСП(2;10;5;100;ЛОЖЬ)+ +ГИПЕРГЕОМ.РАСП(3;10;5;100;ЛОЖЬ)
Примечание : В файле примера плотность вероятности и функция распределения также вычислены с использованием определения и функции ЧИСЛКОМБ() .
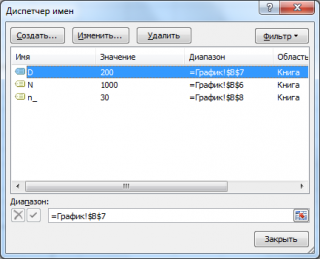
Примечание : Для удобства написания формул в файле примера созданы Имена для параметров Гипергеометрического распределения : n, D и N.
Показатели распределения
В файле примера на листе График имеются формулы для расчета:
- математического ожидания =n*D/N,
- дисперсии (квадрата стандартного отклонения) =n*D/N*(1-D/N)*((N-n)/(N-1)),
- моды =(D+1)*(n+1)/(N+2)
- коэффициента асимметрии .
Аппроксимация Биноминальным распределением
В случае, когда размер совокупности N гораздо больше размера выборки n (т.е., N >> n или n/N<<1), Гипергеометрическое распределение хорошо аппроксимируется Биномиальным распределением с параметрами n (количество испытаний) и p = D / N (вероятность успеха в одном испытании).
Подробнее об этом приближении и об условиях, при которых допустима аппроксимация других распределений, можно прочитать в статье Взаимосвязь некоторых распределений в MS EXCEL .
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
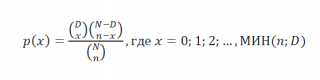
Комментарии