Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.

Немного теории

Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.

Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по простым и сложным процентам.

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования простых процентов изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».

В файле примера приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.

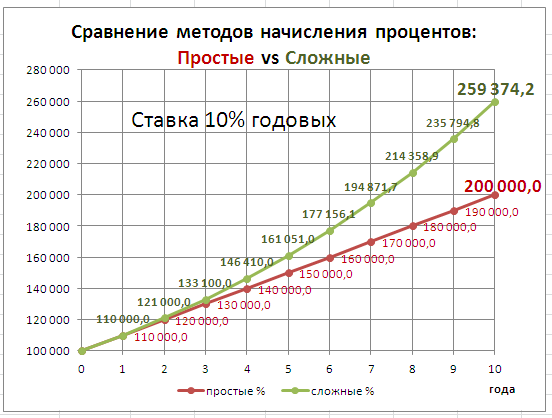
В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов читайте здесь .

Начисление процентов 1 раз в год

Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S - наращенная сумма, i - годовая ставка, n - срок ссуды в годах, (1+ i)^n - множитель наращения.

Начисление процентов несколько раз в год

В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).

В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.

Рассмотрим задачу : Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.

Способ 1. Вычисление с помощью таблицы с формулами Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В файле примера это реализовано на листе Постоянная ставка .

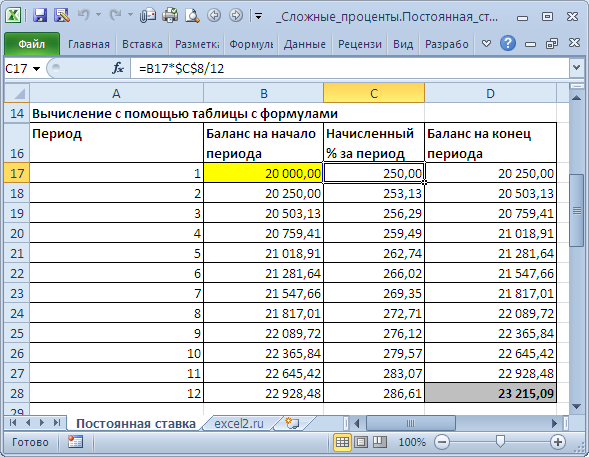
За первый период будут начислены проценты в сумме =20000*(15%/12) , т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.

Способ 2. Вычисление с помощью формулы Наращенных процентов Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию СТЕПЕНЬ() =20000*СТЕПЕНЬ(1+15%/12; 12)

Способ 3. Вычисление с помощью функции БС(). Функция БС() позволяет определить будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае аннуитетных платежей . Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов. =-БС(15%/12;12;;20000)

Или так =-БС(15%/12;12;0;20000;0)

Примечание . В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов используется функция БЗРАСПИС() .

Определяем сумму начисленных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.

Сумма начисленных процентов I равна разности между величиной  наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см. файл примера ).

Определяем Срок долга

Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неизвестного параметра n.

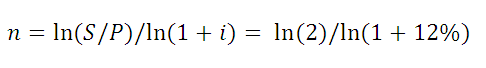
В файле примера приведено решение, ответ 6,12 лет.

Вычисляем ставку сложных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?

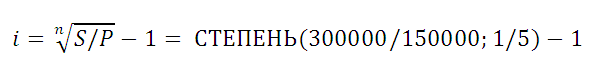
В файле примера приведено решение, ответ 14,87%.

Примечание . Об эффективной ставке процентов читайте в этой статье .

Учет (дисконтирование) по сложным процентам

Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.

Математический учет . В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S - P называется дисконтом.

Пример . Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .

Решение. P = 2000000/(1+15% )^7 Значение текущей стоимости будет меньше, т.к. открыв сегодня вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.

Тот же результат можно получить с помощью формулы =ПС(15%;7;;-2000000;1) Функция ПС() возвращает приведенную (к текущему моменту) стоимость инвестиции и рассмотрена здесь .

Банковский учет . В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл - сложная годовая учетная ставка.

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи Начисление процентов несколько раз в год .

Расчет сложных процентов в случае регулярного пополнения вклада

В файле примера (лист "С поплнением") произведен расчет суммы вклада в случае регулярного пополнения на одну и ту же сумму. Для этого использована функция БС() .

Если сумма вклада пополняется нерегулярно и/или различными платежами, то для расчета необходимо использовать таблицу, которая также приведена в файле примера. Естественно, в случае регулярных и равновеликих платежей итоговые суммы вычисленные с помощью таблицы и функции БС() - совпадают.