Простые проценты в EXCEL

Рассмотрим простые проценты - метод начисления, при котором сумма начисленных процентов определяется исходя только из первоначальной величины вклада (или долга). Процент на начисленные проценты не начисляется (проценты не капитализируются).

Немного теории

Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.

Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по простым процентам и по сложным процентам .

Сущность метода начисления по простым процентам сводится к тому, что проценты начисляются в течение всего срока кредита на одну и ту же величину капитала, предоставленного в кредит (или на одну и ту же величину вклада).

В случае известной годовой процентной ставки (i), суммы капитала, предоставленного в кредит (P) и срока ссуды (n, лет), можно рассчитать так называемую Наращенную сумму S – сумму первоначального капитала (Р) и начисленных на него процентов (I).

Примечание . В случае вклада на определенный срок, S представляет собой Будущую стоимость вклада, вычисленную по методу простых процентов.

Формула определения наращенной суммы с использованием простых процентов (формула простых процентов) записывается в следующем виде: S= P+I= P+P*n*i= P*(1+n*i)

Выражение (1+n*i) называется множителем наращения процентов. В формуле предполагается, что процентная ставка (i) не изменяется в течение всего срока предоставления кредита. В файле примера приведен расчет наращенной суммы для заданного количества лет, годовой % ставке и заданной величине первоначальной суммы. Также приведен график для сравнения наращенной суммы с использованием простых и сложных процентов .

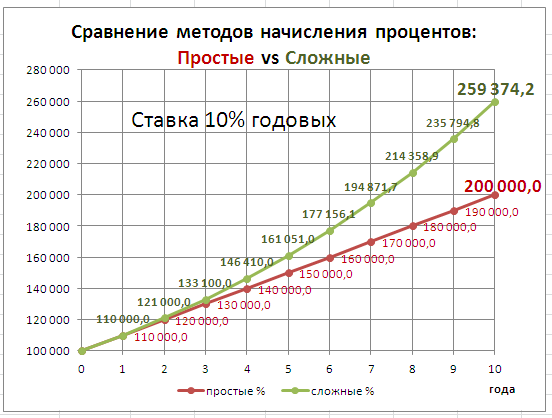
Вычисление наращенной суммы при постоянной процентной ставке

Вышеуказанная формула простых процентов настолько проста, что не понятно, в чем вообще состоит проблема вычислений? Вычислить Наращенную сумму S при известных Р, n, i или вычислить i при известных  Р, n, S можно и на калькуляторе. Однако, все несколько усложняется в случае, когда срок финансовой сделки не равен целому числу лет.

Если срок предоставления кредита определен в месяцах, то формулу для определения наращенной суммы необходимо изменить, разделив годовую ставку i на 12 (12 месяцев в году). Под n теперь будем понимать количество месяцев. S=P*(1+n*i/12) i/12 – это ставка за период (за месяц).

Если срок финансовой сделки определен в кварталах, то под n будем понимать количество кварталов, на который был выдан кредит (или заключен договор срочного вклада). Годовую ставку i нужно разделить на 4 (4 квартала в году). Формула выглядит так: S=P*(1+n*i/4)

По аналогии, можно предположить, что если срок финансовой сделки определен в днях, то под n разумно понимать количество дней, на который был выдан кредит. Однако со ставкой за период не все так просто. Действительно, i нужно делить на 365 (365 дней в году) или на 366 в случае високосного года ? Поэтому, если срок финансовой сделки определен в днях, то формулу определения наращённой суммы записывают несколько в ином виде:

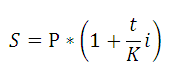
где t — число дней функционирования сделки (число дней, на которое предоставили кредит); К — временная база (число дней в году).

Временную базу года можно брать число дней в году (365 или 366), или даже 360. Откуда 360? Дело в том, что в ряде стран для удобства вычислений год делится на 12 месяцев, по 30 дней в каждом, т.е. продолжительность года К принимается равной 360 дням (12*30).

В этой связи различают три метода процентных расчетов, зависимых от выбранного периода начисления.

1. Точные проценты с точным числом дней ссуды (английский (британский) метод). При этом методе продолжительность года К принимается равной 365 (или 366) дням и определяется фактическое число дней t между двумя датами (датой получения и погашения кредита), т.е. временная база – календарный год.

Примечание . Вычисление по формуле S=P*(1+n*i/365) является лишь приблизительным по английскому методу в случае високосного года (см. ниже).

2. Обыкновенные (обычные) проценты с точным числом дней ссуды (французский метод, банковское правило, гибридный метод). При этом методе величина t рассчитывается, как и в предыдущем методе, а продолжительность года принимается равной К = 360 дням (коммерческий год, обыкновенный год). Это позволяет французским банкирам зарабатывать в 1,01388 раза больше денег, чем английским (365/360= 1,01388) за тот же период.

Примечание . Вычисление по французскому методу можно производить по формуле S=P*(1+n*i/360), где i – годовая ставка, n – число дней ссуды.

3. Обыкновенные проценты с приближенным числом дней ссуды (германский метод). При этом методе величина t определяется так: количество полных месяцев ссуды *умноженное на 30 дней в каждом + точное число дней ссуды в неполных месяцах; продолжительность года К = 360 дней.

В файле примера приведен расчет начисления процентов по 3-м методам.

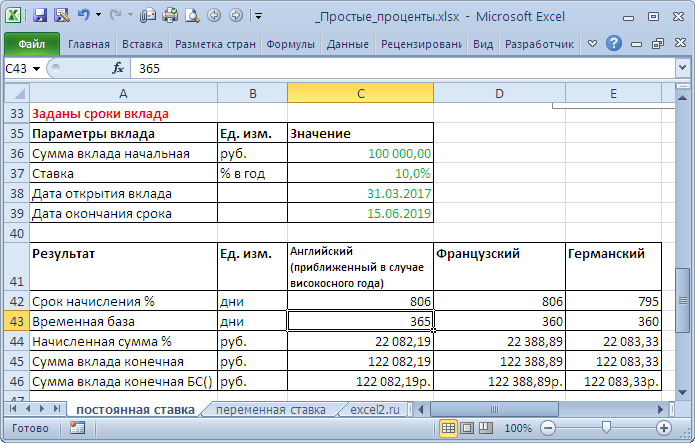
Примечание . При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день.

Понятно, что вычисления по английской и германской системе могут быть сделаны, только если заданы конкретная дата выдачи кредита и дата окончания его срока. Т.к. чтобы вычислить по английской системе – требуется знать продолжительность конкретного года (високосный или нет), а по немецкой – требуется знать количество полных месяцев и число дней ссуды в неполных месяцах. По французскому методу количество дней ссуды берется фактическое, а временная база всегда =360, поэтому вычисления производить можно и без знания конкретных дат (достаточно знать количество дней ссуды). Еще одно замечание о вычислении наращенной суммы при использовании английского метода. Напомним, что продолжительность года в этом методе принимается равной 365 (или 366) дней, правда, не всегда понятно как проводить вычисления, если срок кредита приходится и на високосный и обычный год (например, кредит выдан 31.10.2016, а должен быть погашен в 15.06.2017, високосный 2016). Т.к. в РФ используется английский метод, то ЦЕНТРАЛЬНЫЙ БАНК РОССИЙСКОЙ ФЕДЕРАЦИИ опубликовал письмо от 27 декабря 1999 г. N 361-Т для разъяснения этой ситуации: В случае, если дни периода начисления процентов по привлеченным (размещенным) банками денежным средствам приходятся на календарные годы с разным количеством дней (365 и 366 дней соответственно), то начисление процентов за дни, приходящиеся на календарный год с количеством дней 365, производится из расчета 365 календарных дней в году, а за дни, приходящиеся на календарный год с количеством дней 366, производится из расчета 366 календарных дней в году.

В файле примера в ячейке В50 приведена формула массива , которая позволяет вычислить наращенную сумму в случае кредита, когда года даты выдачи и даты погашения ссуды не совпадают (например, кредит выдан 31.03.2015, а должен быть погашен в 15.06.2017).

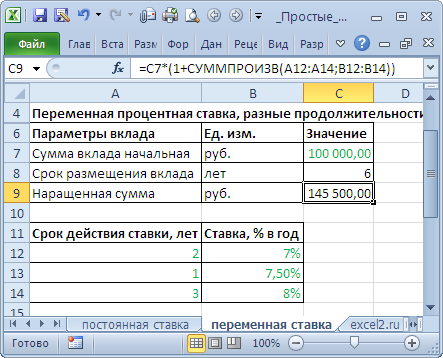
Вычисление наращенной суммы при переменной процентной ставке

При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная ставка определяется по формуле:

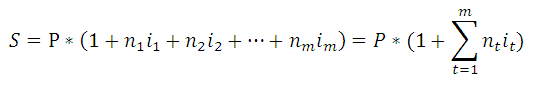
В файле примера на листе Переменная ставка сделаны расчеты по этой формуле: = C7*(1+СУММПРОИЗВ(A12:A14;B12:B14))

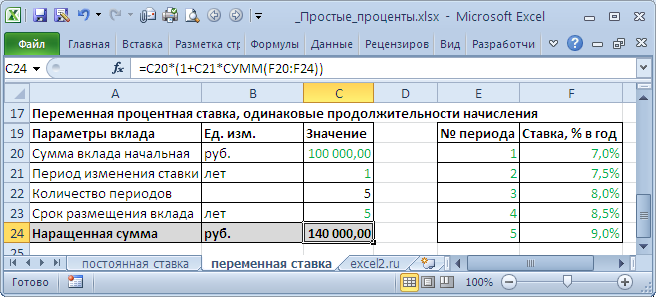
В случае, если процентная ставка изменяется через равные периоды, то вышеуказанную формулу можно несколько упростить.

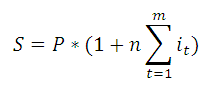
n – период действия ставки без изменения.